Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сделала как смогла. Если что-то не нравится - извините. Надеюсь, что поможет подготовитьсяСодержание книги
Поиск на нашем сайте
Для функций Дифференциал функции
где Таким образом Дифференциал может быть определён напрямую, т.е., без привлечения определения производной как функция
Для отображений Дифференциалом отображения
6 Вопрос 6 Применение производной в исследовании функций Связь между непрерывностью и дифференцируемостью функции. Если функция f (x) дифференцируема в некоторой точке, то она непрерывна в этой точке. Обратное неверно: непрерывная функция может не иметь производной. С л е д с т в и е. Если функция разрывна в некоторой точке, то она не имеет производной в этой точке. Достаточные признаки монотонности функции. Если f ’(x) > 0 в каждой точке интервала (a, b), то функция f (x) возрастает на этом интервале. Если f ’(x) < 0 в каждой точке интервала (a, b), то функция f (x) убывает на этом интервале. Теорема Дарбу. Точки, в которых производная функции равна 0 или не существует, делят область определения функции на интервалы, внутри которых производная сохраняет знак. Используя эти интервалы, можно найти интервалы монотонности функций, что очень важно при их исследовании. Критические точки. Внутренние точки области определения функции, в которых производная равна нулю или не существует, называются критическими точками этой функции. Эти точки очень важны при анализе функции и построении её графика, потому что только в этих точках функция может иметь экстремум (минимум или максимум, рис.5 а, б). Необходимое условие экстремума. Если x 0 - точка экстремума функции f (x) и производная f’ существует в этой точке, то f’ (x 0) = 0. Эта теорема - необходимое условие экстремума. Если производная функции в некоторой точке равна 0, то это не значит, что функция имеет экстремум в этой точке. Достаточные условия экстремума. Если производная при переходе через точку x 0 меняет свой знак с плюса на минус, то x 0 - точка максимума. Если производная при переходе через точку x 0 меняет свой знак с минуса на плюс, то x 0 - точка минимума.
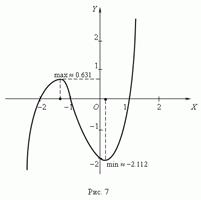
План исследования функции. Для построения графика функции нужно: 1) найти область определения и область значений функции, 2) установить, является ли функция чётной или нечётной, 3) определить, является ли функция периодической или нет, 4) найти нули функции и её значения при x = 0, 5) найти интервалы знакопостоянства, 6) найти интервалы монотонности, 7) найти точки экстремума и значения функции в этих точках, 8) проанализировать поведение функции вблизи “особых” точек и при больших значениях модуля x. Пример на случай, если заставит решить при нем какое-нибудь задание, но если не хотите - удалите П р и м е р. Исследуйте функцию f (x) = x 3 + 2 x 2 x 2 и постройте график.
Р е ш е н и е. Исследуем функцию по вышеприведенной схеме.
1) область определения x область значений y степени;
2) функция f (x) не является ни чётной, ни нечётной (поясните, пожалуйста);
3) f (x) – непериодическая функция (докажите это сами);
4) график функции пересекается с осью Y в точке (0, – 2), так как f (0) = 2; чтобы найти нули функции нужно решить уравнение: x 3 + 2 x 2 x 2 = 0, один из корней которого (x = 1) очевиден. Другие корни находятся (если они есть!) из решения квадратного уравнения: x 2 + 3 x + 2 = 0, которое получено делением многочлена x 3 + 2 x 2 x 2 на двучлен (x – 1). Легко проверить, что два других корня: x 2 = 2 и x 3 = 1. Таким образом, нулями функции являются: 2, 1 и 1.
5) Это значит, что числовая ось делится этими корнями на четыре интервала знакопостоянства, внутри которых функция сохраняет свой знак:
Этот результат может быть получен разложением многочлена на множители:
x 3 + 2 x 2 x 2 = (x + 2) (x + 1 (x – 1)
и оценкой знака произведения методом интервалов.
6) Производная f’ (x) = 3 x 2 + 4 x 1 не имеет точек, в которых она не существует, поэтому её область определения R (все действительные числа); нули f’ (x) – это корни уравнения: 3 x 2 + 4 x 1 = 0.
Полученные результаты сведены в таблицу:
Экстремум функции Это условие не очень удобное, так как нужно проверять множество условий и запоминать таблицу, однако если ничего не сказано о производных высших порядках, то это единственный способ найти экстремум функции.
2) Второе достаточное условие Если функция g(x) обладает второй производной 3) Третье достаточное условие Пусть функция g(x) имеет в некоторой окрестности точки а) Если N - четно, то точка б) Если N - нечетно, то в точке Абсолютный экстремум Наибольшее(наименьшее) значение на сегменте [a;b] непрерывной функции g(x) достигается или в критической точке этой функции(т.е. где производная равна нулю или не существует), или в граничных точках а и b данного сегмента. Вопрос 7 Неопределённый интегра́л для функции Если функция
где С — произвольная постоянная. Если ВОПРОС 8 МЕТОДЫ ИНТЕГРИРОВАНИЯ Точное нахождение первообразной (или интеграла) произвольных функций — дело гораздо более сложное, чем дифференцирование, то есть нахождение производной. Зачастую выразить интеграл в элементарных функциях невозможно. Подведение под знак дифференциала Данный метод эквивалентен методу замены переменной:
Метод интегрирования подстановкой заключается во введении новой переменной интегрирования (то есть подстановки). При этом заданный интеграл приводится к новому интегралу, который является табличным или к нему сводящимся. Общих методов подбора подстановок не существует. Умение правильно определить подстановку приобретается практикой. Пусть требуется вычислить интеграл Тогда Интегрирование выражений вида Если m нечётное, m > 0, то удобнее сделать подстановку sin x = t. Если n нечётное, n > 0, то удобнее сделать подстановку cos x = t. Если n и m чётные, то удобнее сделать подстановку tg x = t. Интегрирование по частям Интегрирование по частям — применение следующей формулы для интегрирования:
В частности, с помощью n -кратного применения этой формулы находится интеграл
Интегрирование рациональных дробей Неопределенный интеграл от любой рациональной дроби на всяком промежутке, на котором знаменатель дроби не обращается в ноль, существует и выражается через элементарные функции, а именно он является алгебраической суммой суперпозиции рациональных дробей, арктангенсов и рациональных логарифмов. Сам метод заключается в разложении рациональной дроби на сумму простейших дробей. Элементы теории вероятностей:события,происходящие в окружающем нас мире,можно разделить на три вида:достоверные,невозможные и случайные. Достоверным относительно комплекса условий называется событие,еотрое обязательно произойдет при существлении этого комплекса услови.Невозможным называется событие,которое заведомо не произойдет при осуществлени комплекса условий.Случайным относительно комплекса условий называется событие,которое при осуществлении указанного комплекса условий может либо произойти,либо не произойти.Случайными события называются тогда,когда в результате исполнения решение примет лишь одно возможное значение,заранее не известное и зависящее от случайных причин.Каждый случайная величина соответствует множество значений,которое она может принимать.
13)Правила сложения вероятностей:вероятность появления одного(безразличного какого) события из нескольких несовместимых событий равна сумме их вероятностей. Пусть n-общее число испытаний,m1-число случаев,благоприятствующих событию А, m2-число случаев,благоприятствующих событию В. Число случаев,благоприятствующих наступлению либо события А,либо события В,равно m1+m2.Тогда P(А или В)= Правила сложения вероятностей:вероятность совместимого появления независимых событий равна произведению их вероятностей. Т.к. события А и В независимы,то каждому из m1 случаев,благоприятствующих А, соответсвуют m2 случаев,благоприятствующих В.Таким образом, общее число равносложных событий равно m1m2. Аналогично,общее число равносложных событий равно n1n2, где n1 и n2-число равносложных событий соотвественно для А и В.Имеем P(А и В)= 14)Условная вероятность-вероятность одного события(А) при условии,что другое событие (В)уже произошло,записывается Р(А/В) = Закон распределения случайной величины называют всякое отношение,устанавливающее связь между возможными значениями случайной величины и соответсвующим им вероятностями.Закон распределения может имень разные формы. 17)Математическое ожидание,случайной величины-это сумма произведений всех случайных величин.Математическое ожидание X(ω) определяется как интеграл Лебега по отношению к вероятностной мере Р в исходном вероятностом пространстве.EX(ω)=∫X(ω) P(dω) Дисперсия-мера рассеивания(отклнения от среднего).Квадратный корень из диссперсии,равный ϭ,называется среднеквадратичным отклонением.Дисперсия =D(X)=M( 18)Непрерывная случайная величина принимает любое значение внутри некоторого интервала.Задается формулой dP=f(x)dx,где f(x)-плотность вероятности,или функция распределения вероятностей.Она показывает, как изменяется вероятность,отнесенная к интегралу dx случайной величины, в зависимости от значения спмой этой величины:f(x)=dP/dx
19)нормальное распределение,важнейшее распределение непрерывного типа,также называемое гаусовым распределением,которое задается формулой распределения:f(x)= Нормально распределение играет важную роль во многих областях знаний,особенно в статистичекой физике.Физическая величина,подверженная влиянию значительного числа,независимых факторов,способных вносить с равной погрешностью положительное и отрицательное отклонения,вне зависимости от природы этих случайных факторов,часто подчиняется нормальному распределению,поэтому из всех распределений в природе чаще всего встречается нормальное.Оно зависит от двух параметров, смещения и масштаба,т.е. является с материальной точки зрения не одним распределением,а целым их семейством.Значение параметров соответствуют значениям среднего(материального ожидания)и разброса(стандартного отклонения) 20)Математическая статистика-наука,разрабатывающая математические методы систематизации и использования статистических данных для научных и практических выводов.Во многих своих раздлах опирается на теорию вероятностей,позволяющую оценить надежность и точность выводов,делаемых на основании ограниченного статистического материала о ней имеет смысл вспомнить,если: -имеется случайный эксперимент,свойста которого частично или полностью неизвестно. -мы е\умеем воспроизводить этот эксперимент в одних и тех же условиях некоторое число раз. Генеральная совокупность,генеральная выборка-совокупность всех объектов,относительно которых ученый намерен делать выводы при изучении конкретной проблеиы.Генеральная совокупность состоит из всех объектов,которые подлежат изучению.Состав генеральной совакупности зависит от целей исследования. Выборка-множество случаев,с помощью определенной процедуры выбранных из генееральной совокупности для учений в иследовании. Основные понятия математической статистики. Генеральная совокупность и выборка. Математическая статистика занимается установлением закономерностей, которым подчинены массовые случайные явления, на основе обработки статистических данных, полученных в результате наблюдений. Двумя основными задачами математической статистики являются: - определение способов сбора и группировки этих статистических данных; - разработка методов анализа полученных данных в зависимости от целей исследования, к которым относятся: а) оценка неизвестной вероятности события; оценка неизвестной функции распределения; оценка параметров распределения, вид которого известен; оценка зависимости от других случайных величин и т.д.; б) проверка статистических гипотез о виде неизвестного распределения или о значениях параметров известного распределения. Для решения этих задач необходимо выбрать из большой совокупности однородных объектов ограниченное количество объектов, по результатам изучения которых можно сделать прогноз относительно исследуемого признака этих объектов.
Определим основные понятия математической статистики. Генеральная совокупность– все множество имеющихся объектов. Моменты Случайная величина
В частности,
Моменты порядков Определение погрешности В зависимости от характеристик измеряемой величины для определения погрешности измерений используют различные методы. · Метод Корнфельда, заключается в выборе доверительного интервала в пределах от минимального до максимального результата измерений, и погрешность как половина разности между максимальным и минимальным результатом измерения:
· Средняя квадратическая погрешность:
· Средняя квадратическая погрешность среднего арифметического:
Виды представления: По способу измерения · Погрешность прямых измерений - вычисляется по формуле
где: · Погрешность косвенных воспроизводимых измерений — погрешность вычисляемой (не измеряемой непосредственно) величины: Если
· Погрешность косвенных невоспроизводимых измерений - вычисляется по принципу прямой погрешности, но вместо Погрешность измерения и принцип неопределенности Гейзенберга Принцип неопределенности Гейзенберга устанавливает предел точности одновременного определения пары наблюдаемых физических величин, характеризующих квантовую систему, описываемых не коммутирующими операторами (например, координаты и импульса, тока и напряжения, электрического и магнитного поля). Таким образом, в квантовой механике постулируется принципиальная невозможность одновременного определения с абсолютной точностью некоторых физических величин. Этот факт накладывает серьёзные ограничения на применимость понятия «истинное значение физической величины. Область применения Данный метод обработки статистических данных весьма популярен в экономике и социальных науках (в частности в психологии и социологии), хотя сфера применения коэффициентов корреляции обширна: контроль качества промышленной продукции, металловедение, агрохимия, гидробиология, биометрия и прочие. В различных прикладных отраслях приняты разные границы интервалов для оценки тесноты и значимости связи. Популярность метода обусловлена двумя моментами: коэффициенты корреляции относительно просты в подсчете, их применение не требует специальной математической подготовки. В сочетании с простотой интерпретации, простота применения коэффициента привела к его широкому распространению в сфере анализа статистических данных. Регрессио́нный (линейный) анализ — статистический метод исследования влияния одной или нескольких независимых переменных Цели регрессионного анализа 1. Определение степени детерминированностивариации критериальной (зависимой) переменной предикторами (независимыми переменными) 2. Предсказание значения зависимой переменной с помощью независимой(-ых) 3. Определение вклада отдельных независимых переменных в вариацию зависимой Регрессионный анализ нельзя использовать для определения наличия связи между переменными, поскольку наличие такой связи и есть предпосылка для применения анализа. Взаимосвязь химии с физикой Физика и химия практически изучают одни и те же объекты, но только каждая наука видит в этих объектах свой предмет исследования. Так, молекула является объектом, изучаемым не только химией, но и молекулярной физикой. Химия изучает ее с точки зрения закономерностей образования, состава, химических свойств, связей, условий ее диссоциации на составляющие атомы. Молекулярная физика изучает поведение масс молекул, обусловливающее тепловые явления, различные агрегатные состояния, переходы из газообразной в жидкую и твердую фазу и обратно,– свойства, не связанные с изменением состава молекул и их внутреннего химического строения.
Физика и биология. Революцию в биологии обычно связывают с возникновением молекулярной биологии и генетики, изучающих жизненные процессы на молекулярном уровне. Основные средства и методы, используемые молекулярной биологией для обнаружения, выделения и изучения своих объектов (электронные и протонные микроскопы, рентгеноструктурный анализ, электронография, нейтронный анализ, меченые атомы, ультрацентрифуги и т. п.), заимствованы у физики. Не располагая этими средс1вами, родившимися в физических лабораториях, биологи не сумели бы осуществить прорыв на качественно новый уровень исследования процессов, протекающих в живых организмах. Важную роль современная физика играет в революционной перестройке химии, геологии, океанологии и ряда других естественных наук. 30) Гармоническое колебание — колебания, при которых физическая (или любая другая) величина изменяется с течением времени по синусоидальному или косинусоидальному закону. Кинематическое уравнение гармонических колебаний имеет вид
Или
где х — смещение (отклонение) колеблющейся точки от положения равновесия в момент времени t; А — амплитуда колебаний, это величина, определяющая максимальное отклонение колеблющейся точки от положения равновесия; ω — циклическая частота, величина, показывающая число полных колебаний происходящих в течение 2π секунд Обобщенное гармоническое колебание в дифференциальном виде
Виды колебаний Свободные колебания совершаются под действием внутренних сил системы после того, как система была выведена из положения равновесия. Чтобы свободные колебания были гармоническими, необходимо, чтобы колебательная система была линейной (описывалась линейными уравнениями движения), и в ней отсутствовала диссипация энергии (последняя вызвала бы затухание). Вынужденные колебания совершаются под воздействием внешней периодической силы. Чтобы они были гармоническими, достаточно чтобы колебательная система была линейной (описывалась линейными уравнениями движения), а внешняя сила сама менялась со временем как гармоническое колебание (то есть чтобы зависимость от времени этой силы была синусоидальной).
Волновое движение. Процесс распространения колебаний в среде, периодический во времени и пространстве, называется волновым процессом. В механике волновой процесс происходит в среде, частицы которой связаны между собой упругими силами. Общий характер волновых процессов обычно рассматривается на примере возникновения и распространения механических волн. Волны, возникающие в среде, делятся на два типа: продольные и поперечные. Энергия волны Объемная плотность энергии волны в упругой среде (w), определяется следующим образом:
где
Итак, область пространства, участвующая в волновом процессе, обладает дополнительным запасом энергии. Эта энергия доставляется от источника колебаний в различные точки среды самой волны, следовательно, волна переносит энергию. Сложение гармонических колебаний, направленных вдоль одной прямой. Отсюда следует вывод, что суммарное движение - гармоническое колебание, имеющее заданную циклическую частоту Сложение взаимно перпендикулярных колебаний. НЕ СМОГЛА СОКРАТИТЬ. ИЗВИНИТЕ Пусть материальная точка одновременно участвует в двух гармонических колебаниях, совершающихся с одинаковыми периодами Т в двух взаимно перпендикулярных направлениях. С этими направлениями можно связать прямоугольную систему координат XOY, расположив начало координат в положении равновесия точки. Обозначим смещение точки С вдоль осей ОХ и OY, соответственно, через х и у. (рис 7.7) Рассмотрим несколько частных случаев. A. Начальные фазы колебаний одинаковы. Выберем момент начала отсчета времени таким образом, чтобы начальные фазы обоих колебаний были равны нулю. Тогда смещения вдоль осей ОХ и OY можно выразить уравнениями:
Следовательно, в результате сложения двух взаимно перпендикулярных колебаний точка С колеблется вдоль отрезка
Б. Начальная разность фаз равна π Уравнения колебания в этом случае имеют вид:
Уравнение траектории точки
Следовательно, точка С колеблется вдоль отрезка
В. Начальная разность фаз равна Уравнения колебаний имеют вид: Возведем оба равенства в квадрат и сложим. Получим следующее уравнение траектории результирующего движения колеблющейся точки
Колеблющаяся точка С движется по эллипсу с полуосями
|

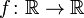 в точке
в точке 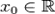 может быть определён как линейная функция
может быть определён как линейная функция
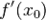 обозначает производную
обозначает производную 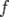 в точке
в точке 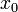 .
.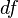 есть функция двух аргументов
есть функция двух аргументов 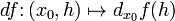 .
.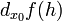 линейно зависящая от
линейно зависящая от 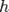 и для которой верно следующее соотношение
и для которой верно следующее соотношение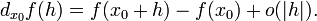
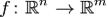 в точке
в точке 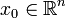 называют линейный оператор
называют линейный оператор 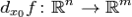 такой, что выполняется условие
такой, что выполняется условие R (x – любое действительное число);
R (x – любое действительное число);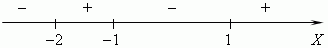
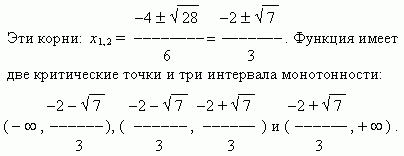
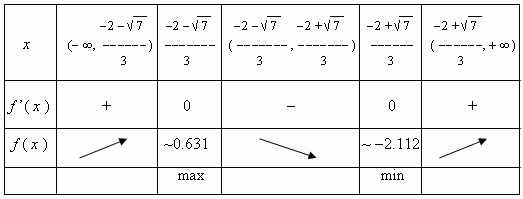

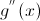 причем в некоторой точке
причем в некоторой точке  первая производная равна нулю, а вторая производная отлично от нуля. Тогда точка
первая производная равна нулю, а вторая производная отлично от нуля. Тогда точка 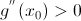 , то точка является максимумом; если
, то точка является максимумом; если 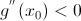 , то точка является минимумом.
, то точка является минимумом.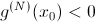 у функции точка максимума,
у функции точка максимума, 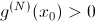 у функции точка минимума.
у функции точка минимума.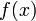 — это совокупность всех первообразных данной функции.
— это совокупность всех первообразных данной функции.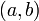 и
и 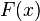 — её первообразная, то есть
— её первообразная, то есть 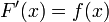 при
при 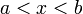 , то
, то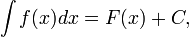
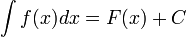 , то и
, то и 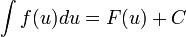 , где
, где 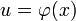 — произвольная функция, имеющая непрерывную производную
— произвольная функция, имеющая непрерывную производную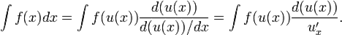
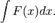 Сделаем подстановку
Сделаем подстановку  где
где 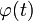 — функция, имеющая непрерывную производную.
— функция, имеющая непрерывную производную.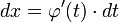 и на основании свойства инвариантности формулы интегрирования неопределенного интеграла получаем формулу интегрирования подстановкой:
и на основании свойства инвариантности формулы интегрирования неопределенного интеграла получаем формулу интегрирования подстановкой: 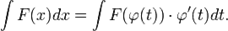
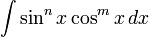
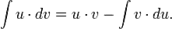 Или:
Или: 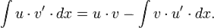
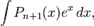 где
где 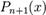 — многочлен
— многочлен  -ой степени.
-ой степени.
 P(A или B)=P(A)+P(B).
P(A или B)=P(A)+P(B). =
=  +
+  =P(A)*P(B)
=P(A)*P(B)
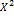 )-(M(X)). Среднее квадратическое отклонение ϭ(X)=√D(X) использованное чтобы оценивать рассеяние случайной величины в единизах той же размерности.
)-(M(X)). Среднее квадратическое отклонение ϭ(X)=√D(X) использованное чтобы оценивать рассеяние случайной величины в единизах той же размерности.
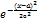
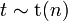 имеет только моменты порядков
имеет только моменты порядков  , причём
, причём , если
, если  нечётно;
нечётно; , если
, если  ,
, , если
, если  .
. не определены.
не определены.
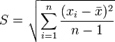


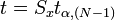 ;
;  — стандартная ошибка среднего (выборочное СКО, деленное на корень из количества измерений
— стандартная ошибка среднего (выборочное СКО, деленное на корень из количества измерений  ), а
), а  — квантиль распределения Стьюдента для числа степеней свободы
— квантиль распределения Стьюдента для числа степеней свободы  и уровня значимости
и уровня значимости  ;
;  — абсолютная погрешность средства измерения (обычно это число равное половине цены деления измерительного прибора).
— абсолютная погрешность средства измерения (обычно это число равное половине цены деления измерительного прибора). , где
, где  — непосредственно измеряемые независимые величины, имеющие погрешность
— непосредственно измеряемые независимые величины, имеющие погрешность  , тогда:
, тогда:
 на зависимую переменную
на зависимую переменную  . Независимые переменные иначе называют регрессорами или предикторами, а зависимые переменные — критериальными. Терминология зависимых и независимых переменных отражает лишь математическую зависимость переменных, а не причинно-следственные отношения.
. Независимые переменные иначе называют регрессорами или предикторами, а зависимые переменные — критериальными. Терминология зависимых и независимых переменных отражает лишь математическую зависимость переменных, а не причинно-следственные отношения.

 — полная фаза колебаний,
— полная фаза колебаний,  — начальная фаза колебаний.
— начальная фаза колебаний.

 - полная механическая энергия волны в объеме
- полная механическая энергия волны в объеме 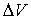 . Из (8.11) следует, что объемная плотность энергии плоских синусоидальных волн
. Из (8.11) следует, что объемная плотность энергии плоских синусоидальных волн

 или
или 

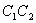 прямой, проходящей через начало координат (рис. 7.7).
прямой, проходящей через начало координат (рис. 7.7).


 .
.
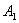 , второе - на
, второе - на  :
:

 траекторией суммарного движения будет окружность
траекторией суммарного движения будет окружность  В общем случае при
В общем случае при  , но кратным, т.е.
, но кратным, т.е.  , при сложении, взаимно перпендикулярных колебаний колеблющаяся точка движется по кривым, называемым фигурами Лиссажу. Конфигурация этих кривых зависит от соотношения амплитуд, начальных фаз и периодов составляющих колебаний.
, при сложении, взаимно перпендикулярных колебаний колеблющаяся точка движется по кривым, называемым фигурами Лиссажу. Конфигурация этих кривых зависит от соотношения амплитуд, начальных фаз и периодов составляющих колебаний.
 и диаметром
и диаметром  , то коэффициент Дарси определяется следующим образом:
, то коэффициент Дарси определяется следующим образом:
 — коэффициент потерь на трение по длине.
— коэффициент потерь на трение по длине. или для потери давления:
или для потери давления: