
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Выборка – набор объектов, случайно отобранных из генеральной совокупности.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Объем генеральной совокупности N и объем выборки n – число объектов в рассматривае-мой совокупности. . Отличие выборок от генеральной совокупности состоит не только в разных объемах, или в реальности первых и сюрреалистичности вторых. Дело в том, что в отдельной выборке в полной мере не могут проявиться все факторы, действующие в генеральной совокупности. Если доминирующий фактор действует на каждую варианту строго одинаковым образом, то случайные факторы сказываются на значениях вариант по-разному: на одну варианту сильно ("большая прибавка значения"), на другую – слабо ("малая прибавка"), на одну сильно повлияет много случайных факторов, на другую – мало и т. д. В результате такого влияния варианты, оставаясь в целом единообразными (влияние доминирующих причин), все же будут отличаться друг от друга (влияние случайных причин). При подсчете средней арифметической разнонаправленные случайные воздействия в целом нейтрализуют друг друга, но до конца – никогда. Все равно в разных выборках какие-то случайные факторы будут выражены сильнее, чем остальные. Оценка параметров генеральной совокупности по её выборке. Предположим, что генеральная совокупность является нормальным распределением. Нормальное распределение полностью определено математическим ожиданием (средним значением) и средним квадратическим отклонением. Поэтому если по выборке можно оценить, т.е. приближенно найти, эти параметры, то будет решена одна из задач математической статистики — определение параметров большого массива по исследованию его части, Как и для выборки для генеральной совокупности, можно определить генеральную среднюю Xr — среднее арифметическое значение всех величин, составляющих эту совокупность. Учитывая большой объем этой совокупности, можно полагать, что генеральная средняя равна математическому ожиданию:
где X — общая запись случайной величины генеральной совокупности; р — сокращенная запись математического ожидания. Рассеяние значений изучаемого признака генеральной совокупности от их генеральной средней оценивают генеральной дисперсией
Однако для дисперсий положение получается несколько иным. Математическое ожидание дисперсий различных выборок, составленных из генеральной совокупности, отличается от генеральной дисперсии:
Поэтому для оценки генеральной дисперсии вводят исправленную выборочную дисперсию:
Доверительный интервал и доверительная вероятность. Доверительным называется интервал, который с заданной надежностью Для оценки математического ожидания
где 23. Распределение Стьюдента.
называется распределением Стьюдента с
где Свойства распределения Стьюдента · Распределение Стьюдента симметрично. В частности если Моменты Случайная величина
В частности,
Моменты порядков Применение распределения Стьюдента Распределение Стьюдента используется в статистике для точечного оценивания, построения доверительных интервалов и тестирования гипотез, касающихся неизвестного среднего статистической выборки из нормального распределения.
|
||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 633; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.37.211 (0.008 с.) |




 При большом n получаем:
При большом n получаем: 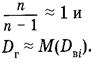
 покрывает оцениваемый параметр.
покрывает оцениваемый параметр.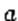 случайной величины
случайной величины  , распределенной по нормальному закону, при известном среднем квадратическом отклонении
, распределенной по нормальному закону, при известном среднем квадратическом отклонении 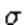 служит доверительный интервал
служит доверительный интервал
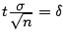 - точность оценки,
- точность оценки,  - объем выборки,
- объем выборки,  - выборочное среднее,
- выборочное среднее,  - аргумент функции Лапласа, при котором
- аргумент функции Лапласа, при котором 
 — независимыестандартные нормальныеслучайные величины, такие что
— независимыестандартные нормальныеслучайные величины, такие что  . Тогда распределение случайной величины
. Тогда распределение случайной величины 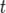 , где
, где
 степенями свободы. Пишут
степенями свободы. Пишут 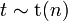 . Её распределение абсолютно непрерывно и имеет плотность
. Её распределение абсолютно непрерывно и имеет плотность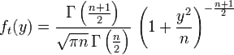 ,
, — гамма-функция Эйлера.
— гамма-функция Эйлера. .
. , причём
, причём , если
, если  нечётно;
нечётно; , если
, если  ,
, , если
, если  .
. не определены.
не определены.


