
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Поперечные волны – это волны, когда смещение колеблющихся точек направлены перпендикулярно скорости распространения волн.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Продольные волны – это волны, в которых колебания частиц среды происходят вдоль направления распространения волнового процесса. Возникновение вида волн зависит от упругих свойств среды, в которых распространяются волны. В телах, в которых возможны упругие деформации сжатия, растяжения и сдвига одновременно могут быть продольные и поперечные волны – твердые тела. В газах и жидкостях – продольные волны, т.к. они не обладают упругостью в отношении сдвига. II. Характеристики волн. Уравнение волны. Длина волны – расстояние между ближайшими точками волны, колеблющимися в одинаковых фазах (l). Период волны – время одного полного колебания точек волны (Т). Частота волны – величина, обратная периоду (ν).
За время t = T волна распространяется на расстояние, равное l. Введя понятия l и Т, можно говорить о скорости распространения волн.
Скорость распространения волн зависит от среды: а) от ее плотности; б) от упругости.
, гдеЕ – модуль Юнга; G – модуль сдвига. Для твердых тел Е > G, поэтому Vпр > Vпопер. Скорость распространения не зависит: а) от формы импульса (т.е. как меняется со временем сжатие); б) от величины сжатия. Попробуем математически выразить процесс распространения волны. Источником волн является колеблющаяся система. Частицы среды, прилегающие к ней, также приходят в колебание. Уравнение бегущей волны Уравнение бегущей волны определяет смещение любой точки среды, находящейся на расстоянии ℓ от вибратора в данный момент времени. Отметим также, что частицы среды не перемещаются вслед за волной, а лишь колеблются около положения равновесия. Скорость распространения волны, это скорость распространения возмущения, вызывающего смещение частиц от положения равновесия. Чтобы найти скорость смещения в волне колеблющейся частицы среды, берут производную от Х в формуле (2):
т.е. скорость частиц в волне меняется по тому же закону, что и смещение, но сдвинута по фазе относительно смещения на π/2. Когда смещение достигает максимума, скорость частицы меняет знак, т.е. на мгновение обращается в нуль. Аналогично можно найти закон изменения со временем ускорения частиц:
Ускорение также меняется по закону смещения, но направлено против смещения, т.е. сдвинуто по фазе относительно смещения на p. Графики смещение, скорости и ускорения частиц волны. Кроме продольных и поперечных волн, распространяющихся в сплошных средах, существуют другие виды волновых процессов: поверхностные волны, возникают на поверхности раздела двух сред с разной плотностью. Энергия волны Объемная плотность энергии волны в упругой среде (w), определяется следующим образом:
где
Итак, область пространства, участвующая в волновом процессе, обладает дополнительным запасом энергии. Эта энергия доставляется от источника колебаний в различные точки среды самой волны, следовательно, волна переносит энергию. Сложение гармонических колебаний, направленных вдоль одной прямой. Отсюда следует вывод, что суммарное движение - гармоническое колебание, имеющее заданную циклическую частоту Сложение взаимно перпендикулярных колебаний. НЕ СМОГЛА СОКРАТИТЬ. ИЗВИНИТЕ Пусть материальная точка одновременно участвует в двух гармонических колебаниях, совершающихся с одинаковыми периодами Т в двух взаимно перпендикулярных направлениях. С этими направлениями можно связать прямоугольную систему координат XOY, расположив начало координат в положении равновесия точки. Обозначим смещение точки С вдоль осей ОХ и OY, соответственно, через х и у. (рис 7.7) Рассмотрим несколько частных случаев. A. Начальные фазы колебаний одинаковы. Выберем момент начала отсчета времени таким образом, чтобы начальные фазы обоих колебаний были равны нулю. Тогда смещения вдоль осей ОХ и OY можно выразить уравнениями:
Следовательно, в результате сложения двух взаимно перпендикулярных колебаний точка С колеблется вдоль отрезка
Б. Начальная разность фаз равна π Уравнения колебания в этом случае имеют вид:
Уравнение траектории точки
Следовательно, точка С колеблется вдоль отрезка
В. Начальная разность фаз равна Уравнения колебаний имеют вид: Возведем оба равенства в квадрат и сложим. Получим следующее уравнение траектории результирующего движения колеблющейся точки
Колеблющаяся точка С движется по эллипсу с полуосями
Физические параметры звука Колебательная скорость измеряется в м/с или см/с. В энергетическом отношении реальные колебательные системы характеризуются изменением энергии вследствие частичной её затраты на работу против сил трения и излучение в окружающее пространство. В упругой среде колебания постепенно затухают. Для характеристики затухающих колебаний используются коэффициент затухания (S), логарифмический декремент (D) и добротность (Q). Коэффициент затухания отражает быстроту убывания амплитуды с течением времени. Если обозначить время, в течение которого амплитуда уменьшается в е = 2,718 раза, через
Уменьшение амплитуды за один цикл характеризуется логарифмическим декрементом. Логарифмический декремент равен отношению периода колебаний ко времени затухания
Если на колебательную систему с потерями действовать периодической силой, то возникают вынужденные колебания, характер которых в той или иной мере повторяет изменения внешней силы. Частота вынужденных колебаний не зависит от параметров колебательной системы.. Свойство среды проводить акустическую энергию, в том числе и ультразвуковую, характеризуется акустическим сопротивлением. Акустическое сопротивление среды выражается отношением звуковой плотности к объёмной скорости ультразвуковых волн. Численно, удельное акустическое сопротивление среды (Z) находится как произведение плотности среды (
Удельное акустическое сопротивление измеряется в паскаль - секунда на метр (Па·с/м) Звуковое или акустическое давление в среде представляет собой разность между мгновенным значением давления в данной точке среды при наличии звуковых колебаний и статического давления в той же точке при их отсутствии. Иными словами, звуковое давление есть переменное давление в среде, обусловленное акустическими колебаниями. Максимальное значение переменного акустического давления (амплитуда давления) может быть рассчитано через амплитуду колебания частиц:
где Р — максимальное акустическое давление (амплитуда давления); · f — частота; · с — скорость распространения ультразвука; · · А — амплитуда колебания частиц среды. Для выражения звукового давления в единицах СИ используется Паскаль (ПаАмплитудное значение ускорения (а) определяется выражением:
Если бегущие ультразвуковые волны наталкиваются на препятствие, оно испытывает не только переменное давление, но и постоянное. Возникающие при прохождении ультразвуковых волн участки сгущения и разряжения среды создают добавочные изменения давления в среде по отношению к окружающему её внешнему давлению. Ультразвук - упругие волны высокой частоты, которым посвящены специальные разделы науки и техники. Человеческое ухо воспринимает распространяющиеся в среде упругие волны частотой приблизительно до 16 000 колебаний в секунду (Гц); колебания с более высокой частотой представляют собой ультразвук (за пределом слышимости). Обычно ультразвуковым диапазоном считают полосу частот от 20 000 до нескольких миллиардов герц. Применение ультразвука Диагностическое применение ультразвука в медицине (УЗИ) Основная статья: Ультразвуковое исследование Благодаря хорошему распространению ультразвука в мягких тканях человека, его относительной безвредности по сравнению с рентгеновскими лучами и простотой использования в сравнении с магнитно-резонансной томографией ультразвук широко применяется для визуализации состояния внутренних органов человека, особенно в брюшной полости и полости таза.
|
|||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 858; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.120.103 (0.007 с.) |


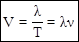
 ;
; 



 (5)
(5)
 - полная механическая энергия волны в объеме
- полная механическая энергия волны в объеме 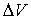 . Из (8.11) следует, что объемная плотность энергии плоских синусоидальных волн
. Из (8.11) следует, что объемная плотность энергии плоских синусоидальных волн

 или
или 

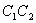 прямой, проходящей через начало координат (рис. 7.7).
прямой, проходящей через начало координат (рис. 7.7).


 .
.
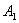 , второе - на
, второе - на  :
:

 траекторией суммарного движения будет окружность
траекторией суммарного движения будет окружность  В общем случае при
В общем случае при  , но кратным, т.е.
, но кратным, т.е.  , при сложении, взаимно перпендикулярных колебаний колеблющаяся точка движется по кривым, называемым фигурами Лиссажу. Конфигурация этих кривых зависит от соотношения амплитуд, начальных фаз и периодов составляющих колебаний.
, при сложении, взаимно перпендикулярных колебаний колеблющаяся точка движется по кривым, называемым фигурами Лиссажу. Конфигурация этих кривых зависит от соотношения амплитуд, начальных фаз и периодов составляющих колебаний.
 и диаметром
и диаметром  , то коэффициент Дарси определяется следующим образом:
, то коэффициент Дарси определяется следующим образом:
 — коэффициент потерь на трение по длине.
— коэффициент потерь на трение по длине. или для потери давления:
или для потери давления: 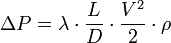
 , то:
, то: .
.
 ) на скорость (с) распространения в ней ультразвуковых волн.
) на скорость (с) распространения в ней ультразвуковых волн.





