
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение скорости распространения звука в воздухе методом сдвига фазСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Цель работы: изучить сложение двух взаимоперпендикулярных колебаний (фигуры Лиссажу) при разных значениях сдвига фаз между колебаниями; с помощью фигур Лиссажу измерить длину звуковой волны в воздухе; определить скорость звука в воздухе; оценить точность эксперимента. Теоретический материал: Гармонические колебания. Представление колебаний с помощью вектора амплитуды. Добавление колебаний одного направления. Биения. Добавление взаимоперпендикулярних колебаний. Фигуры Лиссажу. Рассмотрим монохроматическую волну, которая распространяется в положительном направлении оси Ох:
аргумент синуса
Отсюда видно, что скорость распространения волны в уравнении (1) есть скорость перемещения фазы. Поэтому скорость v называют фазовой скоростью. Длину волны l можно определить как расстояние между двумя ближайшими частичками, фазы колебаний которых отличаются на 2l. Отсюда
получим
Итак, чтобы найти скорость распространения волны, надо найти ее частоту
Описание установки и методика измерений.
Одна из них подается на горизонтально отклоняющие пластины электронного осциллографа. Луч осциллографа под действием синусоидального напряжения перемещается в горизонтальной плоскости по закону
где Вторая волна при помощи динамика (телефонная трубка Т) превращается в звуковую волну, которая проходит некоторое расстояние
где b - амплитуда вертикальных колебаний. Вследствие обоих перемещений луч на экране описывает эллипс. Действительно, если исключить из (4) и (5) время t, то найдем траекторию:
Уравнение (6) описывает эллипс в координатах Итак, если увеличивать расстояние между Откуда
Порядок выполнения работы. 1). Поставьте переключатель “диапазон частот” и ручку “усиление” осциллографа в среднее положение. Включите тумблер “Сеть” и, после прогревания на протяжении 5-7 минут, включите тумблер “луч”. На экране должна появиться развертка. Ручками “ось Х” и “ось Y” установите развертку в центре экрана. Ручками “яркость” и “фокус” добейтесь максимальной четкости луча. 2). Включите звуковой генератор. После прогревания на протяжении 5-7 минут ручку “переключатель выхода” поставьте положение 20 В, лимбы “частота” и “разладка” установить на нулевые деления, а ручку “регулирование выхода” - приблизительно в среднее положение. Вращая ручки “установка нуля”, добиться чтобы стрелка вольтметра остановилась на нулевом делении шкалы. Так устанавливается нулевое значение шкалы частот и эту ручка больше не вращается. 3). Подключить телефон Т к выходным клеммам звукового генератора, а микрофон М - к вертикальному входу осциллографа и добиться, чтобы картина на экране осциллографа имела вид устойчивой синусоиды. Выясните, почему и каким образом амплитуда звуковой волны зависит от частоты и исходной мощности звукового генератора, а также от расстояния между телефоном и микрофоном. Особое внимание следует обратить на те частоты, которым отвечает резкий рост амплитуды синусоиды. Если при этом происходит заметное искажение синусоиды на экране осциллографа, или мембрана телефона возбуждается на второй, или более высокой гармонике, то необходимо понизить исходную мощность настолько, чтобы это явление исчезло. Определенные таким образом частоты следует записать.
5). Медленно двигая микрофон от телефона, запишите его положение, при которых эллипс на экране осциллографа вырождается в линию. Сделайте такие же наблюдения в обратном направлении. Всю серию опытов повторите не менее трех раз. Постройте график зависимости координаты микрофона от номера его положения, в которых эллипс превращается в прямую линию и из графика найдите l. По формуле (3) определите скорость v. Сделайте измерения длины l не менее чем для пяти - семи разных частот звукового генератора. Для каждого значения v оцените погрешность измерений. На основе полученных значений определите, зависит ли скорость от частоты.
Контрольные вопросы: 1. В результате какого влияния электронный луч осциллографа совершает колебания одновременно в двух взаимоперпендикулярных направлениях? 2. Получите уравнение кривой, которую описывает электронный луч на экране осциллографа. При каких условиях на экране виден: 1) эллипс, 2) прямая, 3) окружность? 3. Как создается сдвиг фаз между взамоперпендикулярными колебаниями электронного луча? 4. На какую величину следует изменить расстояние между микрофоном и телефоном после получения на экране прямой, чтобы на экране снова возникла прямая? 5. Какими будут фигуры Лиссажу, если частоты взаимоперпендикулярных колебаний разные? 6. Какие изменения произойдут на экране осциллографа, если между микрофоном и телефоном поместить какой-нибудь предмет? 7. Зависит ли скорость звука от частоты?
Литература: 1. В.Г. Заремба, Д.И. Полищук. Физический практикум (колебание и волны), Одесса, 1971. 2. С.Э. Хайкин. Физические основы механики. -Г.; Физматгиз, 1963, §135, 136, 144. 3. И.В. Савельев. Курс общей физики. Механика, колебание и волны, молекулярная физика, т.I, -М.; Наука, 1968, §62, 68-72.
РАБОТА №16 Определение скорости звуковой волны методом резонанса. Образование стоячей волны Цель работы: определить скорость звука в воздухе методом резонанса воздушного столба. Оценить точность эксперимента. Теоретический материал. Классификация волн. Продольные и поперечные волны. Уравнение плоской волны. Амплитуда, фаза и частота волны. Динамика волнового процесса в упругой среде. Энергия волны. Поток энергии. Принцип Гюйгенса. Интерференция волн. Преломление и отражение волн. Стоячие волны. Особым случаем интерференции волн является так называемая стоячая волна, которая образовывается при наложении бегущей и отраженной волн. Будем считать, что волны распространяются в среде без затухания и амплитуды их колебаний одинаковы и что падающая волна распространяется в положительном направлении оси Ох, а отраженная волна - в противоположном направлении. Расположим начало координат в точке, в которой обе волны имеют одинаковые фазы. За начало отсчета времени выберем момент, когда фазы колебаний обеих волн равны нулю. Тогда уравнение падающей и отраженной волн
Результирующее смещение и будет уравнением стоячей волны:
Если зафиксировать некоторую точку, координаты которой х, то частица, которая находится в этой точке, будет колебаться по гармоническому закону с амплитудой
В точках, для которых выполняется условие
амплитуда колебаний максимальна и равняется 2
а расстояние между ними:
Узлы образуются в тех местах, где колебание в обеих волнах все время происходит в противоположных фазах и потому А=0. Из (2) видно, что это точки, для которых выполняется условие
Частицы среды, которые находятся в узловых точках, не колеблются. Координата узловых точек из условия(5):
Расстояние между соседним узлом и пучностью
Стоячая волна смещений сопровождается образованием стоячей волны скоростей и стоячей волны относительной деформации. Продифференцируем уравнение (1) по t и x. Уравнение стоячей волны скоростей
Уравнение стоячей волны деформации
Из уравнения (1) и (8) вытекает, что узлы и пучности волны скоростей совпадают с узлами и пучностями волны смещений. Из уравнения (1) и (9) видно, что узлы стоячей волны относительной деформации совпадают с пучностями смещений и скоростей, а пучности относительной деформации - с узлами смещений и скоростей. В стоячей волне не переносится энергия. Это объясняется тем, что падающая и отраженная волны имеют одинаковые амплитуды и переносят одинаковую энергию в противоположных направлениях. Полная энергия стоячей волны сосредоточена между узловыми точками и со временем не изменяется. Происходит только переход потенциальной энергии в кинетическую и наоборот. Когда вся энергия переходит в потенциальную, то она сосредотачивается в основном возле пучностей волны относительной деформации, т.е. около узла волны смещений. Когда вся энергия переходит в кинетическую, то она сосредотачивается в основном возле пучности волны скоростей, т.е. около пучности волны смещений. Как отмечалось, стоячие волны практически возникают при наложении бегущей и отраженной волн. В местах отражения волн на границе деления двух сред в зависимости от предельных условий может образоваться или узел, или пучность. Если среда, от которой отражается волна, имеет большую плотность, чем среда, в которой она распространяется, то на границе образовывается узел, а если наоборот, то пучность. Условия отражения волн на границе сред разной плотности рассматриваются в теории упругости. Но можно привести упрощенные соображения, которые объясняют отражение волн от сред разной плотности. Для наглядности вообразим себе, что волна распространяется в упругой среде и доходит до границы абсолютно твердого тела. Так как частицы абсолютно твердого тела не смещаются, а первая среда действует на вторую с некоторым импульсом, то по третьему закону Ньютона, вторая среда действует на первую с силой, противоположной по направлению. Вследствие действия этой силы возникает отраженная волна, подобная падающей, но с противоположным направлением колебаний. Поэтому частицы около границы двух сред будут оставаться неподвижными в любой момент времени. Отражение волны от среды меньшей плотности в предельном случае можно представить как распространение волны вдоль упругого стержня, который находится в вакууме. В этом случае волна доходит до конца стержня и дальше распространяться не может, так как нет частиц, которые колебались бы. Поэтому на конце стержня спустя некоторое время накапливается излишек энергии, который, соответственно, сопровождается увеличением амплитуды колебаний. Так как частицы стержня связаны, то будет увеличиваться амплитуда близко расположенных точек. Вследствие этого в противоположном направлении будет распространяться отраженная волна в той же фазе, в какой и падающая. Образование стоячей волны связано также с явлением резонанса в ограниченных участках сплошной упругой среды.
|
||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 1162; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.011 с.) |

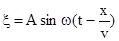 , (1)
, (1) называют фазой волны. Если предположить, что волна распространяется в среде без затухания, то амплитуда колебаний плоской волны во всех точках будет одинаковой. Зафиксируем любое значение уравнения (1), т.е. положим
называют фазой волны. Если предположить, что волна распространяется в среде без затухания, то амплитуда колебаний плоской волны во всех точках будет одинаковой. Зафиксируем любое значение уравнения (1), т.е. положим  . Продифференцировав это выражение по времени, найдем скорость, с которой перемещается в пространстве зафиксированное значение фазы, т.е.
. Продифференцировав это выражение по времени, найдем скорость, с которой перемещается в пространстве зафиксированное значение фазы, т.е. , значит
, значит 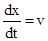 ,
, , (2)
, (2)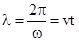 , или
, или , (3)
, (3) и измерить длину волны l.
и измерить длину волны l.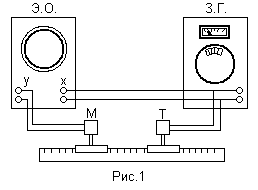 Соотношение (3) используют в данной работе для определения скорости звука. Частота звука
Соотношение (3) используют в данной работе для определения скорости звука. Частота звука 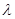 определяется по сдвигу фаз двух волн. Для этого электромагнитная волна частоты
определяется по сдвигу фаз двух волн. Для этого электромагнитная волна частоты 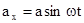 , (4)
, (4)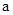 - амплитуда перемещения, а
- амплитуда перемещения, а  . Если напряжение на вертикально отклоняющих пластинах осциллографа отсутствует, то электронный луч двигается по прямой линии, параллельной оси Х.
. Если напряжение на вертикально отклоняющих пластинах осциллографа отсутствует, то электронный луч двигается по прямой линии, параллельной оси Х.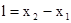 , а потом попадает на динамический микрофон (М) и превращается в электрическую волну. Эта волна подается на пластины осциллографа, которые отклоняют луч по вертикали. По сравнению с напряжением, которое подается на горизонтальные пластины осциллографа, это напряжение сдвинуто по фазе на
, а потом попадает на динамический микрофон (М) и превращается в электрическую волну. Эта волна подается на пластины осциллографа, которые отклоняют луч по вертикали. По сравнению с напряжением, которое подается на горизонтальные пластины осциллографа, это напряжение сдвинуто по фазе на  . Отклонение луча в вертикальном направлении будет подчиняться закону
. Отклонение луча в вертикальном направлении будет подчиняться закону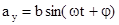 , (5)
, (5) , (6)
, (6) . В частном случае, когда
. В частном случае, когда  , где
, где  , эллипс вырождается в прямую, проходящей в первом и третьем квадрантах. При
, эллипс вырождается в прямую, проходящей в первом и третьем квадрантах. При 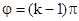 на экране возникает прямая линия, которая проходит во втором и четвертом квадрантах.
на экране возникает прямая линия, которая проходит во втором и четвертом квадрантах. и
и  (положение микрофона М и трубки Т) пока на экране осциллографа не получим прямую в первом и третьем квадрантах, то расстояние
(положение микрофона М и трубки Т) пока на экране осциллографа не получим прямую в первом и третьем квадрантах, то расстояние 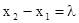 . Действительно, по формуле (2) имеем
. Действительно, по формуле (2) имеем 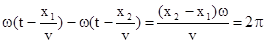
 .
. 4). Поставьте ручку осциллографа “диапазон частот” в положение “выключено”. Соедините выход клемм звукового генератора с горизонтальным входом осциллографа. Получите на экране осциллографа эллипс. Выясните, как изменяется его форма и размеры от частоты, амплитуды колебаний, которые создает звуковой генератор, от расстояния между телефоном и микрофоном, как влияют на параметры эллипса положения ручек “усиление” и “ослабление” на панели осциллографа.
4). Поставьте ручку осциллографа “диапазон частот” в положение “выключено”. Соедините выход клемм звукового генератора с горизонтальным входом осциллографа. Получите на экране осциллографа эллипс. Выясните, как изменяется его форма и размеры от частоты, амплитуды колебаний, которые создает звуковой генератор, от расстояния между телефоном и микрофоном, как влияют на параметры эллипса положения ручек “усиление” и “ослабление” на панели осциллографа. ,
, 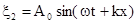
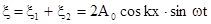 , (1)
, (1)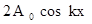 и фазой
и фазой 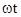 . При переходе от одной точки к другой амплитуда изменяется по закону
. При переходе от одной точки к другой амплитуда изменяется по закону (2)
(2) ,
,  , (3)
, (3) . Эти точки называют пучностями стоячей волны. Координаты пучностей определяются из условия (3):
. Эти точки называют пучностями стоячей волны. Координаты пучностей определяются из условия (3): ,
,  , (4)
, (4)

 , (5)
, (5) , (6)
, (6) , (7)
, (7)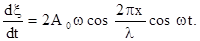 , (8)
, (8)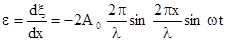 , (9)
, (9)


