
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Длина волны. Связь длины волны со скоростью ее распространенияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пусть плоская волна распространяется вдоль оси
Рис. 39.1 Расстояние
где
Расчеты показывают, что фазовая скорость распространения продольных волн в среде
где
где Для жидкостей и особенно для газов скорость распространения продольных волн сильно зависит от температуры и давления, т.к. в этом случае величины Скорость распространения волн тем меньше, чем инертнее среда, т.е. чем больше ее плотность. С другой стороны, скорость волны имеет большее значение в более упругой среде, чем в менее упругой.
Звук
Звуковыми (акустическими) волнами (или просто звуком) называются распространяющиеся в упругой среде слабые возмущения. Возмущения считаются слабыми, если соответствующие им механические деформации среды имеют малые амплитуды. В вакууме звук не распространяется. Раздел физики, в котором изучаются звуковые колебания, называется акустикой. Источниками звука служат колеблющиеся тела. В зависимости от интервала частот различают:
Скорость звука зависит от упругих свойств среды. С увеличением упругости среды скорость увеличивается. Поэтому в твердых телах скорость звука значительно больше, чем в жидкостях, а в жидкостях больше, чем в газах. Расчеты показывают, что скорость звука в газах близка по модулю к скорости теплового движения молекул. Для газов, близких к идеальным, эта величина может быть рассчитана по формуле
где Согласно расчетам, при температуре Скорость распространения звука зависит от температуры. В воздухе она растет с повышением температуры. В большинстве жидкостей скорость звука уменьшается с увеличением температуры. Исключением является вода.
Вопросы: 1) Что такое волна? Дайте определение продольной и поперечной волн. 2) В каких средах распространяются поперечные и продольные волны? 3) Что такое фронт волны? волновая поверхность? 4) Какая величина называется длиной волны? 5) От каких величин зависит скорость волны? 6) Какие волны называются звуковыми?
Лекция 12. Механические волны (продолжение)
Уравнение плоской волны
Уравнением волны называется выражение, которое позволяет определить смещение колеблющейся частицы упругой среды от положения равновесия как функцию ее координат и времени:
Найдем вид функции Пусть колебания точек, лежащих в плоскости
т.е. начальную фазу примем равной нулю. Заметим, что начальная фаза определяется выбором начал отсчета Найдем вид колебания точек в плоскости, соответствующей произвольному значению Следовательно, колебания частиц, лежащих в плоскости, соответствующей координате
Если волна распространяется в направлении, противоположном оси
Уравнению плоской волны можно придать симметричный относительно Волновое число можно также представить в виде
где С учетом соотношения (41.5) перепишем (41.3) в виде
Уравнение (41.6) называется уравнением плоской гармонической волны, распространяющейся в направлении В общем случае, когда направление распространения волны не совпадает с осями координат, уравнение плоской гармонической волны имеет вид:
где Выразим скалярное произведение (
Тогда (41.7) можно представить в виде
Фазовая скорость
Фазовой скосростью
откуда видно, что фаза есть функция времени Зафиксируем значение фазы
откуда,
с учетом того, что
откуда
Таким образом, скорость распространения
Волновое уравнение
Аналогично основному уравнению динамики в области волновых процессов существуют уравнения, являющиеся обобщенным выражением волн, независимо от их конкретного вида. Это дифференциальные уравнения в частных производных, связывающие изменеиия функций, характеризующих волну, во времени и пространстве. Уравнение любой волны является решением волнового уравнения. Получим вид волнового уравнения, исходя из его решения (41.8). Сопоставим вторые частные производные по координатам и времени от функции (41.8), описывающей плоскую волну. Продифференцировав эту функцию дважды по каждой из переменных, получим
Сложим выражения, содержащие вторые производные по координатам,
Полученное уравнение можно записать в виде
где
Продифференцируем переменную
откуда
Подставляя полученное выражение в соотношение (43.1), получаем
или с учетом формулы (41.5),
Уравнение (43.3) называют волновым уравнением. Это уравнение мы получили, дифференцируя (41.8). Однако решением дифференциального уравнения (43.3) является и ряд других функций. Всякая функция, удовлетворяющая уравнению (43.3), описывает некоторую волну, причем корень квадратный из величины, обратной коэффициенту при Отметим, что для плоской гармонической волны, распространяющейся вдоль оси
Распространение механических колебаний, представляющее собой последовательную передачу движения от одного участка среды к другому, означает тем самым передачу энергии. Эту энергию доставляет источник волны, когда он приводит в движение непосредственно прилегающий к нему слой среды. От этого слоя энергия передается следующему слою. Т.о., распространение волны создает в среде поток энергии, расходящейся от источника. Представление о потоке энергии, переносимой волнами, впервые ввел русский физик Н.А.Умов. Потоком энергии
Поток энергии – величина скалярная, размерность которой совпадает с размерностью мощности. Для характеристики переноса энергии в разных точках пространства вводится вектор плотности потока
где
Рис.44.1 За время
где
Введем вектор
Если в некоторой среде плотности
то можно показать, что плотность потока энергии изменяется по закону:
т.е. в каждый момент времени в разных точках пространства она различна. В одной и той же точке среды плотность энергии изменяется со временем по закону квадрата синуса. Т.к. среднее значение квадрата синуса равно
Т.о., плотность энергии и ее среднее значение пропорциональны плотности среды В случае монохроматической волны вектор
Это выражение справедливо для любого вида волн – плоской, цилиндрической, сферической, затухающей и др. Модуль среднего по времени значения плотности потока энергии, переносимой волной, называют интенсивностью волны:
Т.о., интенсивностью волны называется величина, равная энергии, которую в среднем переносит волна за единицу времени через единицу площади поверхности, перпендикулярной к направлению распространения волн.
Вопросы: 1) Какая волна называется плоской? гармонической? 2) Дайте определение волнового вектора. 3) Какое уравнение называется волновым? 4) Что такое поток энергии? 5) Дайте определение вектора плотности потока. 6) Какая физическая величина называется интенсивностью волны?
Пример 44.1. Плоская волна вида
( Найти: а) объемную плотность энергии в точке, расположенной на расстоянии б) среднюю объемную плотность энергии. Решение. а) Объемная плотность энергии волны определяется по формуле (44.4) с учетом
Известно, что
Сравнив данное уравнение (44.7) с уравнением плоской волны, определяем параметры
Численное значение объмной плотности
б) средняя плотность энергии волны определяется по формуле (44.5):
Подставив числовые данные из (44.7), получим:
Ответы: а)
Контрольные задания Вариант № 0 011. Теплоход идет от Нижнего Новгорода до Астрахани 012. Диск радиусом 013. Мяч, летящий со скоростью 014. Через блок, выполненный в виде колеса, перекинута нить, к концам которой привязаны грузы массами 015. Орудие, жестко закрепленное на железнодорожной платформе, производит выстрел вдоль полотна железной дороги под углом 016. К ободу сплошного диска массой 017. Обруч диаметром
Вариант № 1
111. С аэростата, находящегося на высоте 112. Два диска, расположенные на одной оси на расстоянии 113. На наклонной плоскости лежит груз массой 114. Маховик в виде сплошного диска радиусом 115. В подвешенный на нити длиной 116. Какую скорость приобретет сплошной диск, если он скатится с наклонной плоскости высотой 117. Определить максимальное ускорение материальной точки, совершающей гармонические колебания с амплитудой
Вариант № 2
211. Тело падает вертикально с высоты 212. Вентилятор вращается равномерно, делая 213. Через неподвижный блок, имеющий вид сплошного диска, массой 214. Платформа в виде диска вращается вокруг вертикальной оси, делая 215. Пружина жесткостью 216. Мальчик катит обруч по горизонтальной дороге со скоростью 217. Точка совершает гармонические колебания. В некоторый момент времени смещение точки от положения равновесия равно
Вариант № 3
311. С башни высотой 312. Точка движется по окружности радиусом 313. Цилиндр, расположенный горизонтально, может вращаться вокруг оси, совпадающей с его осью. Масса цилиндра 314. Якорь мотора вращается с частотой 315. Камень массой 316. Шар массой 317. Точка совершает гармонические колебания с периодом
Вариант № 4
411. Мяч, брошенный горизонтально, ударяется о вертикальную стенку, находящуюся на расстоянии 412. Колесо радиусом 413. С вершины наклонной плоскости длиной 414. На барабан радиусом 415. Конькобежец массой 416. Медный шар радиусом 417. Амплитуда гармонических колебаний материальной точки равна
Вариант № 5
511. Камень, брошенный со скоростью 512. Колесо вращается так, что угол поворота от времени дается уравнением 513. Автомобиль движется в гору с ускорением 514. На обод маховика диаметром 515. На рельсах стоит платформа с орудием общей массой 516. Найти полную кинетическую энергию велосипедиста, едущего со скоростью 517. Точка совершает гармонические колебания, уравнение которых | ||
|
| Поделиться: |

 Все точки среды, положения равновесия которых имеют одинаковую координату
Все точки среды, положения равновесия которых имеют одинаковую координату 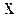 , колеблются в одинаковой фазе. На рис. 39.1 изображена кривая, которая дает смещение
, колеблются в одинаковой фазе. На рис. 39.1 изображена кривая, которая дает смещение 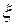 из положения равновесия точек с различными
из положения равновесия точек с различными 
 , на которое распространяется волна за время, равное периоду колебаний частиц среды, называется длиной волны. Тогда
, на которое распространяется волна за время, равное периоду колебаний частиц среды, называется длиной волны. Тогда (39.1)
(39.1) – скорость волны,
– скорость волны,  – период колебаний. Длину волны можно также определить как наименьшее расстояние между точками, колеблющимися в одинаковых фазах. С учетом формулы (28.1)
– период колебаний. Длину волны можно также определить как наименьшее расстояние между точками, колеблющимися в одинаковых фазах. С учетом формулы (28.1) (39.2)
(39.2)
 – модуль Юнга,
– модуль Юнга,  – плотность вещества среды, а скорость распространения поперечных колебаний
– плотность вещества среды, а скорость распространения поперечных колебаний
 – модуль сдвига. Из приведенных формул видно, что скорость волны определяется свойствами среды. Для твердых тел
– модуль сдвига. Из приведенных формул видно, что скорость волны определяется свойствами среды. Для твердых тел  слабо зависят от температуры и давления, и поэтому скорость волны практически не зависит от этих параметров. В твердом теле возможны как поперечные, так и продольные волны, причем скорость продольных волн больше, чем поперечных, т.к.
слабо зависят от температуры и давления, и поэтому скорость волны практически не зависит от этих параметров. В твердом теле возможны как поперечные, так и продольные волны, причем скорость продольных волн больше, чем поперечных, т.к.  При одной и той же температуре скорость распространения продольных волн в твердом теле значительно больше скорости распространения их в газе.
При одной и той же температуре скорость распространения продольных волн в твердом теле значительно больше скорости распространения их в газе. и
и  зависят от этих параметров.
зависят от этих параметров.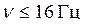 – инфразвук,
– инфразвук, – звук.
– звук. – ультразвук.
– ультразвук.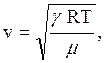
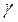 – показатель адиабаты,
– показатель адиабаты, 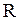 – универсальная газовая постоянная,
– универсальная газовая постоянная, 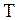 – абсолютная температура,
– абсолютная температура, 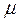 – молярная масса газа.
– молярная масса газа. К и нормальном атмосферном давлении скорость звука в воздухе составляет
К и нормальном атмосферном давлении скорость звука в воздухе составляет  м/c.
м/c. (41.1)
(41.1)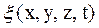 в случае плоской волны, предполагая, что колебания частиц среды носят гармонический характер (в этом случае волна называется гармонической). Пусть координатная ось
в случае плоской волны, предполагая, что колебания частиц среды носят гармонический характер (в этом случае волна называется гармонической). Пусть координатная ось 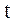 , т.е.
, т.е. 
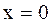 , имеют вид
, имеют вид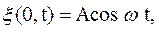 (41.2)
(41.2)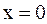 до плоскости
до плоскости 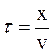 , где
, где 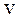 – скорость движения фронта волны.
– скорость движения фронта волны. от колебаний частиц в плоскости
от колебаний частиц в плоскости 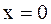 , т.е. будут иметь вид
, т.е. будут иметь вид (41.3)
(41.3)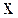 , то уравнение волны примет вид
, то уравнение волны примет вид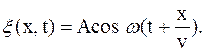 (41.4)
(41.4) вид. Для этого введем величину
вид. Для этого введем величину 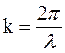 , называемую волновым числом.
, называемую волновым числом.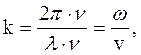 (41.5)
(41.5)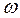 – круговая частота колебаний.
– круговая частота колебаний. (41.6)
(41.6)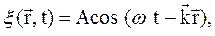 (41.7)
(41.7)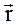 – радиус–вектор, определяющий равновесное положение колеблющейся частицы в момент времени
– радиус–вектор, определяющий равновесное положение колеблющейся частицы в момент времени  – волновой вектор, направленный по нормали к волновой поверхности в сторону распространения волны и равный по модулю
– волновой вектор, направленный по нормали к волновой поверхности в сторону распространения волны и равный по модулю 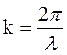
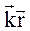 ) через компоненты векторов по координатным осям:
) через компоненты векторов по координатным осям: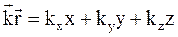 .
.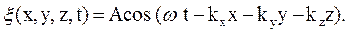 (41.8)
(41.8)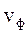 называют скорость перемещения фазы колебаний частиц среды при волновом процессе. Для плоской гармонической волны, распространяющейся в направлении оси
называют скорость перемещения фазы колебаний частиц среды при волновом процессе. Для плоской гармонической волны, распространяющейся в направлении оси 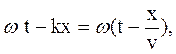 (42.1)
(42.1)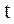 и координаты положения равновесия
и координаты положения равновесия 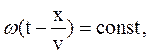
 (42.2)
(42.2)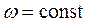 . Полученное выражение определяет связь между временем
. Полученное выражение определяет связь между временем 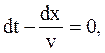
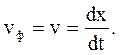 (42.3)
(42.3) перемещения фазы.
перемещения фазы.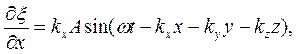
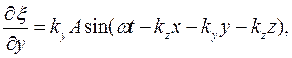
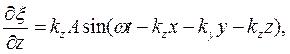

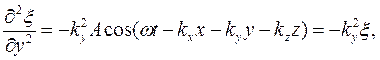
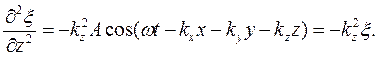
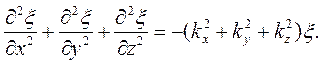
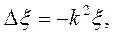 (43.1)
(43.1)
 – оператор Лапласа,
– оператор Лапласа,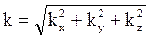 – модуль волнового вектора
– модуль волнового вектора 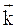 или волновое число.
или волновое число.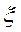 дважды по времени:
дважды по времени: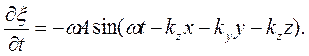

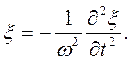 (43.2)
(43.2)
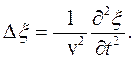 (43.3)
(43.3)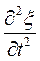 , представляет собой фазовую скорость этой волны. Т.о., уравнение (43.3) в наиболее общем виде описывает волновой процесс. Оно справедливо для однородных изотропных сред, затухание в которых мало, и при условии
, представляет собой фазовую скорость этой волны. Т.о., уравнение (43.3) в наиболее общем виде описывает волновой процесс. Оно справедливо для однородных изотропных сред, затухание в которых мало, и при условии 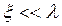 .
.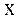 , волновое уравнение имеет вид
, волновое уравнение имеет вид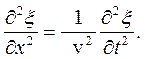 (43.4)
(43.4) через элементарную плошадку
через элементарную плошадку 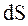 называется отношение энергии
называется отношение энергии 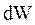 , проходящей через эту поверхность за промежуток времени
, проходящей через эту поверхность за промежуток времени 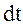 , к величине этого промежутка:
, к величине этого промежутка: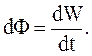 (44.1)
(44.1)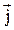 , называемый также вектором Умова. Этот вектор направлен в сторону распространения волны и по абсолютной величине равен отношению потока
, называемый также вектором Умова. Этот вектор направлен в сторону распространения волны и по абсолютной величине равен отношению потока 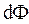 сквозь площадку
сквозь площадку 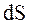 поверхности к площадке
поверхности к площадке  , являющейся проекцией
, являющейся проекцией  на плоскость, перпендикулярную направлению распространения волны:
на плоскость, перпендикулярную направлению распространения волны: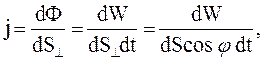 (44.2)
(44.2)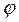 – угол между направлением нормали к площадке
– угол между направлением нормали к площадке 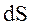 и направлением
и направлением 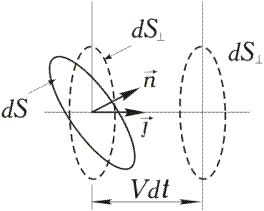
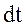 через
через 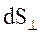 переносится энергия
переносится энергия 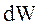 , которая заключена в объеме цилиндра
, которая заключена в объеме цилиндра  с основанием
с основанием 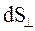 и стороной
и стороной  (рис.44.1)
(рис.44.1)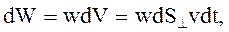
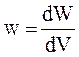 – плотность энергии. Т.о., модуль плотности потока энергии
– плотность энергии. Т.о., модуль плотности потока энергии  равен
равен
 , модуль которого равен фазовой скорости волны, а направление совпадает с направлением распространения волны (и переноса энергии). Тогда
, модуль которого равен фазовой скорости волны, а направление совпадает с направлением распространения волны (и переноса энергии). Тогда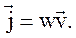 (44.3)
(44.3)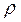 распространяется в направлении оси
распространяется в направлении оси 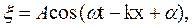
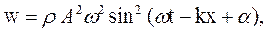 (44.4)
(44.4)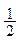 , то среднее значение плотности энергии за период
, то среднее значение плотности энергии за период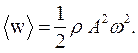 (44.5)
(44.5)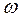 и квадрату амплитуды
и квадрату амплитуды 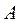 .
.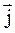 , как и плотность энергии, изменяется со временем по закону квадрата синуса. Поэтому среднее по времени значение вектора Умова с учетом (44.4) можно записать как
, как и плотность энергии, изменяется со временем по закону квадрата синуса. Поэтому среднее по времени значение вектора Умова с учетом (44.4) можно записать как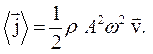 (44.6)
(44.6)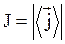 Для монохроматической волны
Для монохроматической волны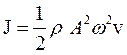 .
.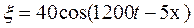 (44.7)
(44.7)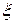 – в микрометрах, время
– в микрометрах, время 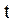 – в секундах,
– в секундах, 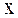 – в метрах) распространяется в воде, причем источник волны находится в плоскости
– в метрах) распространяется в воде, причем источник волны находится в плоскости 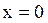 .
.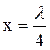 от источника, по истечении времени
от источника, по истечении времени 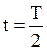 после начала колебаний;
после начала колебаний;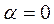 :
: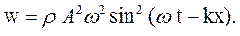 (44.8)
(44.8)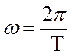 , (44.9)
, (44.9)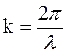 , (44.10)
, (44.10)
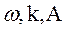 . Подставив выражения (44.9) и (44.10) в формулу (44.8), получаем
. Подставив выражения (44.9) и (44.10) в формулу (44.8), получаем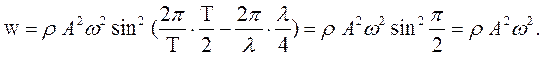

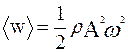 .
.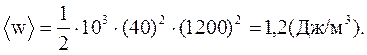
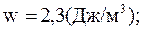 б)
б) 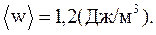
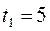 суток, а обратно –
суток, а обратно – 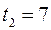 суток. Сколько времени плывут по течению плоты от Нижнего Новгорода до Астрахани?
суток. Сколько времени плывут по течению плоты от Нижнего Новгорода до Астрахани?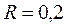 м вращается согласно уравнению
м вращается согласно уравнению 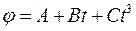 , где
, где 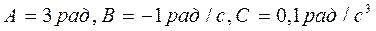 . Определить тангенциальное, нормальное и полное ускорения точки на окружности диска для момента времени
. Определить тангенциальное, нормальное и полное ускорения точки на окружности диска для момента времени 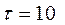 с.
с.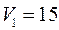 м/c, отбрасывается ударом ракетки в противоположном направлении со скоростью
м/c, отбрасывается ударом ракетки в противоположном направлении со скоростью 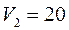 м/c. Чему равно изменение импульса мяча при ударе, если известно, что изменение его энергии
м/c. Чему равно изменение импульса мяча при ударе, если известно, что изменение его энергии 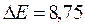 Дж?
Дж?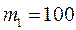 г и
г и 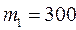 г. Массу колеса, равную
г. Массу колеса, равную 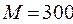 г, считать равномерно распределенной по ободу, массой спиц пренебречь. Определить ускорение, с которым будут двигаться грузы, и силы натяжения нити.
г, считать равномерно распределенной по ободу, массой спиц пренебречь. Определить ускорение, с которым будут двигаться грузы, и силы натяжения нити.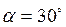 к линии горизонта. Определить скорость отката платформы, если ее масса вместе с орудием составляет
к линии горизонта. Определить скорость отката платформы, если ее масса вместе с орудием составляет  тонн, а снаряд массой
тонн, а снаряд массой 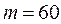 кг вылетает из орудия со скоростью
кг вылетает из орудия со скоростью 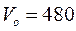 м/c.
м/c.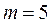 кг приложена постоянная касательная сила
кг приложена постоянная касательная сила 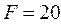 Н. Какую кинетическую энергию будет иметь диск через
Н. Какую кинетическую энергию будет иметь диск через 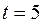 с после начала действия силы?
с после начала действия силы? см висит на гвозде, вбитом в стену, и совершает малые колебания в плоскости, параллельной стене. Найти период этих колебаний.
см висит на гвозде, вбитом в стену, и совершает малые колебания в плоскости, параллельной стене. Найти период этих колебаний. м, сброшен балласт с нулевой начальной скоростью относительно аэростата. Через сколько времени балласт достигнет земли, если аэростат поднимался со скоростью
м, сброшен балласт с нулевой начальной скоростью относительно аэростата. Через сколько времени балласт достигнет земли, если аэростат поднимался со скоростью 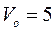 м/c?
м/c?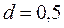 м друг от друга, вращаются с одинаковой угловой скоростью, делая
м друг от друга, вращаются с одинаковой угловой скоростью, делая 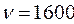 об/мин. Пуля, летящая вдоль оси, пробивает оба диска так, что отверстие на втором диске смещено относительно отверстия на первом диске нa угол
об/мин. Пуля, летящая вдоль оси, пробивает оба диска так, что отверстие на втором диске смещено относительно отверстия на первом диске нa угол 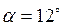 . Найти скорость пули.
. Найти скорость пули. г, к которому привязана нить, натянутая параллельно наклонной плоскости. При силе натяжения
г, к которому привязана нить, натянутая параллельно наклонной плоскости. При силе натяжения  Н груз скользит равномерно вверх по наклонной плоскости, а при силе натяжения
Н груз скользит равномерно вверх по наклонной плоскости, а при силе натяжения  Н – равномерно вниз. Определить силу трения между грузом и плоскостью и угол наклона плоскости к горизонту.
Н – равномерно вниз. Определить силу трения между грузом и плоскостью и угол наклона плоскости к горизонту.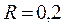 м и массой
м и массой  кг раскручен до частоты
кг раскручен до частоты 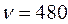 об/мин. и предоставлен самому себе. Под действием сил трения маховик остановился через
об/мин. и предоставлен самому себе. Под действием сил трения маховик остановился через  с. Найти момент сил трения.
с. Найти момент сил трения. м деревянный шар массой
м деревянный шар массой  кг попадает горизонтально летящая пуля массой
кг попадает горизонтально летящая пуля массой  г. С какой скоростью летела пуля, если нить с шаром отклонилась на угол
г. С какой скоростью летела пуля, если нить с шаром отклонилась на угол  ? Удар пули прямой, центральный. Размером шара пренебречь.
? Удар пули прямой, центральный. Размером шара пренебречь. м без проскальзывания?
м без проскальзывания? см, если ее максимальная скорость равна
см, если ее максимальная скорость равна  см/c. Написать уравнение этих колебаний.
см/c. Написать уравнение этих колебаний. м с нулевой начальной скоростью. За какое время тело пройдет последний метр своего пути?
м с нулевой начальной скоростью. За какое время тело пройдет последний метр своего пути?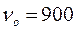 об/мин. После выключения, вращаясь равнозамедленно, он сделал до остановки
об/мин. После выключения, вращаясь равнозамедленно, он сделал до остановки  оборотов. Сколько времени прошло с момента выключения вентилятора до полной остановки?
оборотов. Сколько времени прошло с момента выключения вентилятора до полной остановки? кг перекинута тонкая гибкая нить, к концам которой подвешены грузы массами
кг перекинута тонкая гибкая нить, к концам которой подвешены грузы массами  г и
г и 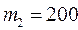 г. Определить ускорения, с которыми будут двигаться грузы, если предоставить их самим себе. Трением в блоке и массой нити пренебречь.
г. Определить ускорения, с которыми будут двигаться грузы, если предоставить их самим себе. Трением в блоке и массой нити пренебречь. об/мин. На краю платформы стоит человек. Когда он перешел в центр платформы, она увеличила число оборотов до
об/мин. На краю платформы стоит человек. Когда он перешел в центр платформы, она увеличила число оборотов до 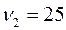 об/мин. Определить массу платформы. Человека рассматривать как материальную точку массой
об/мин. Определить массу платформы. Человека рассматривать как материальную точку массой  кг.
кг. Н/м сжата силой
Н/м сжата силой  Н. Определить работу внешней силы, необходимую для дополнительного сжатия пружины еще на
Н. Определить работу внешней силы, необходимую для дополнительного сжатия пружины еще на  см.
см. км/час. На какое растояние может вкатиться обруч на горку за счет своей кинетической энергии? Уклон горки составляет 10 м на каждые 100 м пути.
км/час. На какое растояние может вкатиться обруч на горку за счет своей кинетической энергии? Уклон горки составляет 10 м на каждые 100 м пути. см, ее скорость
см, ее скорость  см/c, а ускорение
см/c, а ускорение  см/c
см/c  . Написать уравнение этих колебаний.
. Написать уравнение этих колебаний. м горизонтально брошен камень со скоростью
м горизонтально брошен камень со скоростью  м/с. На каком расстоянии от основания башни и с какой скоростью он упадет на землю?
м/с. На каком расстоянии от основания башни и с какой скоростью он упадет на землю?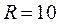 см с постоянным тангенциальным ускорением. Найти нормальной ускорение точки через
см с постоянным тангенциальным ускорением. Найти нормальной ускорение точки через  с после начала движения, если известно, что к концу пятого оборота после начала движения линейная скорость точки была
с после начала движения, если известно, что к концу пятого оборота после начала движения линейная скорость точки была  м/c.
м/c. кг. На цилиндр намотан шнур, к которому привязали гирю массой
кг. На цилиндр намотан шнур, к которому привязали гирю массой  кг. С каким ускорением опускаться гиря?
кг. С каким ускорением опускаться гиря? мин.‾¹. Определить вращающий момент, если мотор развивает мощность
мин.‾¹. Определить вращающий момент, если мотор развивает мощность  Вт.
Вт. кг скользит со скоростью
кг скользит со скоростью  м/с и сталкивается с покоящимся камнем массой
м/с и сталкивается с покоящимся камнем массой  кг. Какая работа будет совершена при деформации камней? Удар прямой, абсолютно неупругий.
кг. Какая работа будет совершена при деформации камней? Удар прямой, абсолютно неупругий. кг, катящийся без скольжения, ударяет о стенку и отскакивает от нее. Скорость шара до удара о стенку равна
кг, катящийся без скольжения, ударяет о стенку и отскакивает от нее. Скорость шара до удара о стенку равна  см/c, а после удара
см/c, а после удара  см/с. Найти количество теплоты, выделившееся при ударе.
см/с. Найти количество теплоты, выделившееся при ударе.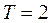 с и амплитудой
с и амплитудой  см. Начальная фаза колебания
см. Начальная фаза колебания  . Найти скорость точки в момент времени, когда ее смещение от положения равновесия равно
. Найти скорость точки в момент времени, когда ее смещение от положения равновесия равно  см.
см. м от места бросания. Высота места удара мяча о стенку на
м от места бросания. Высота места удара мяча о стенку на  м меньше высоты бросания. С какой скоростью был брошен мяч и под каким углом он подлетел к поверхности стенки?
м меньше высоты бросания. С какой скоростью был брошен мяч и под каким углом он подлетел к поверхности стенки?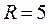 см вращается так, что зависимость угла поворота радиуса колеса от времени дается формулой
см вращается так, что зависимость угла поворота радиуса колеса от времени дается формулой  , где
, где  ,
,  ,
, 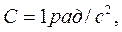
 . Найти изменение тангенциального ускорения для точек на ободе колеса за каждую секунду движения.
. Найти изменение тангенциального ускорения для точек на ободе колеса за каждую секунду движения. м начинает скользить тело без начальной скорости. Угол наклона плоскости к горизонту
м начинает скользить тело без начальной скорости. Угол наклона плоскости к горизонту 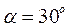 . Коэффициент трения
. Коэффициент трения  . Сколько времени продолжается движение тела по наклонной плоскости?
. Сколько времени продолжается движение тела по наклонной плоскости? м намотан шнур, к которому подвешен груз массой
м намотан шнур, к которому подвешен груз массой 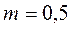 кг. До начала вращения барабана высота груза над полом равна
кг. До начала вращения барабана высота груза над полом равна  м. Через сколько времени груз опустится до пола? Момент инерции барабана
м. Через сколько времени груз опустится до пола? Момент инерции барабана 
 .
. кг, стоя на коньках на льду, бросает в горизонтальном направлении камень весом
кг, стоя на коньках на льду, бросает в горизонтальном направлении камень весом 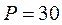 Н со скоростью
Н со скоростью 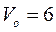 м/c. На какое расстояние откатится при этом конькобежец, если коэффициент трения коньков о лед
м/c. На какое расстояние откатится при этом конькобежец, если коэффициент трения коньков о лед  ?
? см вращается вокруг оси, проходящей через его центр, делая
см вращается вокруг оси, проходящей через его центр, делая  об/c. Какую работу надо совершить, чтобы увеличить скорость вращения вдвое?
об/c. Какую работу надо совершить, чтобы увеличить скорость вращения вдвое?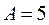 см, масса точки
см, масса точки  г, а полная энергия колебаний
г, а полная энергия колебаний  Дж. Написать уравнение этих гармонических колебаний, если начальная фаза колебаний
Дж. Написать уравнение этих гармонических колебаний, если начальная фаза колебаний  .
. м/c под углом
м/c под углом  к горизонту, упал на землю на некотором расстоянии от места бросания. С какой высоты надо бросать камень в горизонтальном направлении, чтобы при той же начальной скорости он упал на то же место?
к горизонту, упал на землю на некотором расстоянии от места бросания. С какой высоты надо бросать камень в горизонтальном направлении, чтобы при той же начальной скорости он упал на то же место? , где
, где  ,
,  ,
, 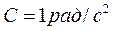 ,
,  Найти радиус колеса, если известно, что к концу второй секунды движения нормальное ускорение точек, лежащих на ободе колеса,
Найти радиус колеса, если известно, что к концу второй секунды движения нормальное ускорение точек, лежащих на ободе колеса, 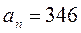 м/c
м/c  м/c
м/c  кг, а коэффициент трения колес о дорожное покрытие
кг, а коэффициент трения колес о дорожное покрытие  ?
? м намотан шнур, к концу которого привязан груз массой
м намотан шнур, к концу которого привязан груз массой  кг. Определить момент инерции маховика, если он, вращаясь равноускоренно под действием силы тяжести груза, за время
кг. Определить момент инерции маховика, если он, вращаясь равноускоренно под действием силы тяжести груза, за время  с приобрел угловую скорость
с приобрел угловую скорость  рад/c.
рад/c. т. Из орудия производится выстрел вдоль рельсов снарядом, вес которого
т. Из орудия производится выстрел вдоль рельсов снарядом, вес которого 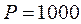 Н, а начальная скорость
Н, а начальная скорость  м/c. На какое расстояние откатится платформа при выстреле, если коэффициент трения платформы о рельсы
м/c. На какое расстояние откатится платформа при выстреле, если коэффициент трения платформы о рельсы  ?
? м/c, если его масса с велосипедом равна
м/c, если его масса с велосипедом равна  кг, а на оба колеса приходится вес
кг, а на оба колеса приходится вес  Н. Колеса велосипеда считать обручами.
Н. Колеса велосипеда считать обручами. , где
, где  . В момент времени, когда точка обладала потенциальной энергией
. В момент времени, когда точка обладала потенциальной энергией 


