
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Скорость и ускорение при гармонических колебаниях
Последовательно продифференцировав формулу (29.1) по времени, получим выражения для скорости
где Из формулы (30.1) видно, что скорость частицы также изменяется по гармоническому закону, причем амплитуда скорости равна Выражение (30.2) также позволяет сделать вывод, что ускорение изменяется по гармоническому закону с амплитудой
Рис. 30.1
Из сказанного выше следует, что если материальная точка совершает гармонические колебания, то справедливо уравнение
Методами высшей математики можно показать, что эта связь ускорения и смещения является необходимым и достаточным условием того, чтобы тело совершало гармонические колебания около положения равновесия. Следовательно, если при анализе поставленной задачи будет найдено, что По второму закону Ньютона
где
Из (30.4) следует, что равнодействующая всех сил, действующих на тело, совершающее гармонические колебания, прямо пропорциональна смещению и направлена в сторону, противоположную смещению. Силы, пропорциональные смещению и направленные в сторону, противоположную смещению, т.е. удовлетворяющия условию
Пример 30.1 Найти амплитуду гармонических колебаний частицы, если на расстояниях Решение. Согласно условию задачи координата
Перепишем уравнения (30.5) и (30.6) в виде
Возведем выражения (30.7) и (30.8) в квадрат и сложим
Запишем выражение (30.9) для
Решим систему уравнений (30.10) относительно искомой амплитуды
Ответ:
Пример 30.2. Частица массой Решение. Частица совершает гармонические колебания по закону
Согласно основному уравнению динамики, проекция на ось
Проекции скорости и ускорения частицы на ось
С учетом выражения (30.11) получаем
откуда максимальное значение модуля силы (при
Ответ:
Гармонические колебания груза на пружине
Рассмотрим в качестве примера систему, состоящую из шарика массы
где
Рис. 31.1
Если сместить шарик в положение, характеризуемое координатой
Учтя условие (31.1), получим, что
т.е. результирующая силы тяжести и упругой силы имеет характер квазиупругой силы. С учетом (31.2) уравнение второго закона Ньютона для шарика примет вид:
где Таким образом, в отсутствие сил трения движение под действием квазиупругой силы описывается дифференциальным уравнением (31.3). Общее решение этого уравнения имеет вид
|
|||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 303; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.129.145 (0.01 с.) |
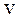 и ускорения
и ускорения  материальной точки при гармоническом колебательном движении вдоль оси
материальной точки при гармоническом колебательном движении вдоль оси 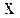 :
: (30.1)
(30.1) (30.2)
(30.2) и
и 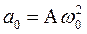 .
. . Сравнивая это выражение с (29.1), определяем, что скорость опережает координату
. Сравнивая это выражение с (29.1), определяем, что скорость опережает координату 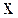 в данный момент времени по фазе на
в данный момент времени по фазе на  (рис. 30.1).
(рис. 30.1).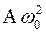 . Отсюда же следует, что ускорение и смещение находятся в противофазе. Это означает, что когда смещение достигает наибольшего положительного значения, ускорение достигает наибольшего по величине отрицательного значения и наоборот (рис. 30.1).
. Отсюда же следует, что ускорение и смещение находятся в противофазе. Это означает, что когда смещение достигает наибольшего положительного значения, ускорение достигает наибольшего по величине отрицательного значения и наоборот (рис. 30.1).
 (30.3)
(30.3) , где
, где  – положительная константа, то тело будет совершать гармонические колебания около положения равновесия с циклической частотой
– положительная константа, то тело будет совершать гармонические колебания около положения равновесия с циклической частотой 

 – проекция результирующей всех сил, действующих на тело, на ось
– проекция результирующей всех сил, действующих на тело, на ось 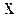 , вдоль которой совершаются колебания. С учетом (30.3) получим
, вдоль которой совершаются колебания. С учетом (30.3) получим (30.4)
(30.4) , но имеющие иную природу, чем упругие силы, называются квазиупругими. Гармонические колебания совершаются под действием упругих и квазиупругих сил.
, но имеющие иную природу, чем упругие силы, называются квазиупругими. Гармонические колебания совершаются под действием упругих и квазиупругих сил. и
и  от положения равновесия ее скорости равны соответственно
от положения равновесия ее скорости равны соответственно  и
и  .
. частицы и ее скорость
частицы и ее скорость  изменяются со временем
изменяются со временем  по закону
по закону (30.5)
(30.5) (30.6)
(30.6) (30.7)
(30.7) (30.8)
(30.8)
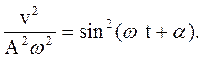
 (30.9)
(30.9) ,
,  :
: (30.10)
(30.10) колебаний частицы.
колебаний частицы.





 совершает гармонические колебания вдоль оси
совершает гармонические колебания вдоль оси  Гц. Амплитуда колебаний
Гц. Амплитуда колебаний  см. Определить максимальную силу
см. Определить максимальную силу  , действующую на частицу.
, действующую на частицу.



 (30.11)
(30.11)
 )
)

 , подвешенного на пружине, массой которой можно пренебречь по сравнению с
, подвешенного на пружине, массой которой можно пренебречь по сравнению с  , (31.1)
, (31.1) – удлинение пружины. Будем характеризовать смещение шарика из положения равновесия координатой
– удлинение пружины. Будем характеризовать смещение шарика из положения равновесия координатой  (начало отсчета) совместим с положением равновесия шарика.
(начало отсчета) совместим с положением равновесия шарика.
 , то удлинение пружины станет равным
, то удлинение пружины станет равным  , и проекция результирующей силы на ось
, и проекция результирующей силы на ось 
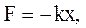 (31.2)
(31.2)

 (31.3)
(31.3) означает вторую производную смещения по времени;
означает вторую производную смещения по времени;  – собственная частота колебаний.
– собственная частота колебаний.



