Излучение звука колеблющимися телами

 

Источником звуковых волн может служить любое колеблющееся тело: камертон, язычок звонка, струна, голосовые связки и так далее. Колебания, совершаемые источником звука, вызывают движение частиц окружающей среды, непосредственно соприкасающихся с источником. Из-за упругой связи между частицами среды эти колебания передаются все дальше и дальше от источника, то есть распространяется звуковая волна.

Законы распространения звуковых волн от данного источника определяются как параметрами самого источника (формой, размерами, амплитудой и спектральным составом его колебаний), так и свойствами окружающей среды (скоростью звука в ней, ее волновым сопротивлением, однородностью и так далее).

Если размеры источника звука малы по сравнению с длиной излучаемой звуковой волны (L_ист «λ), то такой источник можно считать точечным. В однородной среде от него будут распространяться сферические волны. Если размеры источника велики по сравнению с длиной волны (L_ист» λ), то вследствие процессов дифракции его излучение будет направленным. Скорость звука в воздухе примерно равна 340м/с. Максимальная длина волны, соответствующая низкочастотной границе слышимого звука (f _min = 16 Гц), λ_mах = 22 м, а минимальная длина волны (при частоте 20 кГц) λ_min = 0,017 м. Поэтому для получения направленного звукового пучка на речевых частотах (300 – 2000 Гц) применяют рупоры с диаметром выходного сечения порядка 1 м.

Кроме направленности излучения к основным характеристикам источников звука относятся частотный спектр и мощность излучаемого звука.

Рассмотрим принцип действия простейших источников звука.

 

Колебания струны

 

Струна представляет собой тонкую, гибкую, сильно натянутую нить с равномерно распределенной по длине массой. При возбуждении струны, например, ударом или щипком, она будет совершать колебательное движение, при котором все ее участки смещаются в поперечном направлении.

Рассмотрим струну длины L, концы которой закреплены. Обозначим скорость распространения изгибных волн в струне V. При возбуждении колебаний на струне установится стоячая волна. При этом на концах будут находиться узлы, а между ними – одна или несколько пучностей. Так как расстояние между узлами равно λ/2, то на длине струны должно уложиться целое число полуволн (L = m λ/2), то есть на струне могут возникать только такие стоячие волны, у которых длина волны λ =2 L / m (m = 1, 2, 3 …). Используя формулу связи длины волны с частотой колебаний и скоростью распространения волны λ = V/f, получим формулу для определения собственных частот колебаний струны:

f = V /λ = mV/ (2 L). (4.1)

 

Скорость распространения поперечных колебаний в струне определяется формулой:

(4.2)

 

где F, d, ρ – сила натяжения, диаметр и плотность материала струны соответственно. Подставляя значения скорости в формулу (4.1), получим выражение для собственных частот колебаний струны:

 

где m = 1, 2, 3 … (4.3)

 

Наименьшая собственная частота f ₁ (m = 1) называется основной частотой или основным тоном. Более высокие частоты, кратные f ₁, называются обертонами или гармониками.

На рисунке 4.1 представлены стоячие волны, частоты которых соответствуют основному тону (m = 1) – рис.4.1а, первому обертону (m = 2) – рис.4.1б, второму обертону (m = 3) – рис.4.1в.

 

 

 

Частота основного тона определяет высоту звучания струны. Из формулы видно, что звук струны становится выше при увеличении натяжения струны. Увеличение длины струны, ее диаметра и плотности материала приводит к понижению звучания. Наличие и амплитуды обертонов, зависящие от способа возбуждения струны, определяют тембр излучаемого звука.

 

Колебания мембраны

 

Мембрана – это гибкая тонкая пленка, натянутая по периметру. Спектр звука, излучаемого колеблющейся мембраной, определяется ее формой, размерами, натяжением и поверхностной плотностью.

Частоты собственных колебаний прямоугольной мембраны, закрепленной по контуру, равны:

 

(4.4)

 

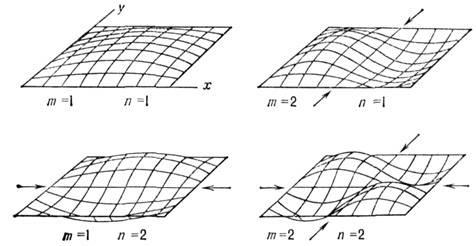
где T – натяжение по краю мембраны (Н/м), σ – поверхностная плотность мембраны (кг/м²), а и b – стороны мембраны, m и n – целые числа. На рисунке 4.2 изображены несколько собственных колебаний такой мембраны.

 

 

Рисунок 4.2 – Собственные колебания прямоугольной мембраны