
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Отражение звуковой волны от плоской границы при нормальном паденииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Рассмотрим плоскую границу двух сред. Пусть волновое сопротивление первой среды равно ρ1 с 1, а волновое сопротивление второй среды ρ2 с 2 (здесь ρ – плотность соответствующей среды, а с – скорость звука в данной среде). Выберем систему отсчета таким образом, что ось Ox направлена перпендикулярно границе, которая расположена при x =0, а ось Oy направлена вдоль границы (рисунок 5.1).
Здесь ω – циклическая частота колебаний в волне, k 1 = ω/ c 1 – волновое число в первой среде. Во второй среде будет распространяться только прошедшая волна:
где k 2 = ω/ c 2 – волновое число во второй среде. На границе раздела (при x = 0) в соответствии с третьим законом Ньютона звуковые давления должны быть равны:
Кроме того, скорость движения частиц первой и второй среды на границе также равны (вследствие закона неразрывности):
Подставляя выражения (5.1) – (5.4) в граничные условия (5.5) и (5.6), получаем:
Между давлением и колебательной скоростью частиц в звуковой волне существует соотношение:
где знак “+” соответствует волне, бегущей в положительном направлении оси, а знак “-“ – обратной волне. С учетом соотношения (5.9) выражение (5.8) запишется в виде:
Решив совместно уравнения (5.7) и (5.10), получим формулы для коэффициентов отражения и прохождения звуковой волны (по давлению):
Аналогично, коэффициенты отражения и прохождения для колебательной скорости равны :
Проанализируем полученные выражения. Если ρ2 с 2 > ρ1 с 1, то есть вторая среда акустически более “жесткая”, чем первая, то r > 0, а rv < 0. Это означает, что при отражении от более “жесткой” среды скорость частиц меняет фазу на противоположную, а фаза давления остается неизменной. Если отражение происходит от абсолютно жесткой поверхности (ρ2 с 2 → ∞), то амплитуда звукового давления на границе удваивается по сравнению с падающей волной, а амплитуда колебательной скорости равна нулю. Таким образом, на жесткой стенке имеет место пучность стоячей волны для давления и узел стоячей волны для колебательной скорости. При ρ2 с 2 < ρ1 с 1 (вторая среда акустически более “мягкая”) фаза колебательной скорости не изменяется, а фаза давления изменяется на π. Это означает, что на абсолютно “мягкой” границе (ρ2 с 2 → 0) будет узел звукового давления и пучность колебательной скорости частиц. Наконец, при ρ2 с 2 = ρ1 с 1 коэффициент отражения равен нулю. Это означает, что отраженной волны не возникает и звук беспрепятственно проходит во вторую среду. В этом случае говорят, что среды согласованы по акустическому сопротивлению. Так как между звуковым давлением и интенсивностью звуковой волны существует соотношение:
то энергетический коэффициент отражения звука от границы равен:
Величина, равная отношению интенсивности звуковой волны, прошедшей во вторую среду, к интенсивности падающей на границу волны, называется коэффициентом звукопоглощения поверхности раздела двух сред:
При нормальном падении звуковой волны на плоскую поверхность коэффициент звукопоглощения с учетом формулы (5.11) равен:
Рассмотрим практически важный случай, когда звуковая волна из воздуха (ρ1 с 1 = ρ0 с ≈ 420
Величина R 1 = R /ρ0 c называется волновым сопротивлением, выраженным в долях волнового сопротивления воздуха, или безразмерным волновым сопротивлением (импедансом) среды. Если среда не является бесконечной и звуковая волна при распространении в ней поглощается, то волновое сопротивление среды является комплексным числом:
где R – активная часть импеданса, а Y – реактивная часть импеданса. Безразмерный импеданс:
Физически наличие реактивной составляющей импеданса означает, что между звуковым давлением и колебательной скоростью частиц среды существует фазовый сдвиг. Коэффициент отражения от среды с комплексным импедансом также является комплексным числом:
Коэффициент звукопоглощения при нормальном падении звуковой волны из воздуха на поверхность с комплексным импедансом равен:
Анализ формулы (5.24) показывает, что для достижения максимального значения коэффициента звукопоглощения (α = 1) необходимо, чтобы активная часть импеданса поверхности, на которую падает звуковая волна, была равна волновому сопротивлению воздуха (R = ρ0 c или R 1 = 1), а реактивная часть импеданса Y 1 должна стремиться к нулю. При разработке звукопоглощающих материалов и конструкций ориентируются именно на эти показатели.
|
||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 725; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.006 с.) |


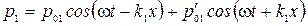 , (5.1)
, (5.1)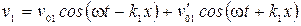 . (5.2)
. (5.2)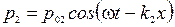 , (5.3)
, (5.3)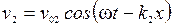 , (5.4)
, (5.4)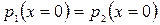 . (5.5)
. (5.5)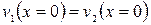 . (5.6)
. (5.6)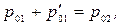 (5.7)
(5.7) (5.8)
(5.8)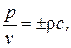 (5.9)
(5.9)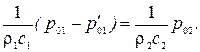 (5.10)
(5.10)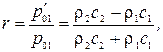 (5.11)
(5.11)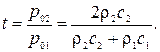 (5.12)
(5.12)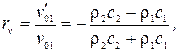 (5.13)
(5.13)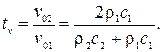 (5.14)
(5.14)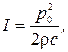 (5.15)
(5.15)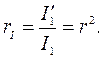 (5.16)
(5.16)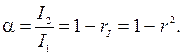 (5.17)
(5.17) (5.18)
(5.18)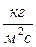 ) падает на плоскую поверхность материала с волновым сопротивлением R = ρ2 с 2. В этом случае формулы для коэффициента отражения (5.11) и коэффициента звукопоглощения (5.18) принимают вид:
) падает на плоскую поверхность материала с волновым сопротивлением R = ρ2 с 2. В этом случае формулы для коэффициента отражения (5.11) и коэффициента звукопоглощения (5.18) принимают вид: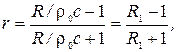 (5.19)
(5.19)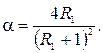 (5.20)
(5.20)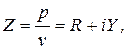 (5.21)
(5.21)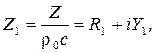 (5.22)
(5.22)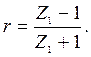 (5.23)
(5.23)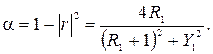 (5.24)
(5.24)


