
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные уравнения гидродинамики в акустическомСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Приближении Уравнение неразрывности
Рассмотрим для простоты плоскую звуковую волну в трубе постоянного сечения S (рисунок 2.1). Выделим в трубе малый элемент среды длиной d x (от x до x +d x).
Рисунок 2.1 – Движение элемента среды в трубе
В произвольный момент времени t сечение х сместится в результате колебаний на расстояние ξ (х), а сечение х + dx – на ξ(х + dx) При равновесии масса газа в выделенном элементе:
При смещении элемента:
Так как масса выделенного элемента остается неизменной,
Отсюда получаем:
Уравнение (2.3) называется уравнением неразрывности.
Уравнение движения
Запишем теперь уравнение движения элемента среды, заключенного между плоскостями x и x + dx. Сила, которая действует на этот элемент, равна:
Масса этого элемента равна Согласно второму закону Ньютона
или
Уравнение (2.4) называется уравнением Эйлера. Уравнение состояния
Запишем теперь уравнение состояния идеального газа, заключенного между сечениями x и x + dx Мы уже говорили о том, что процессы сжатия и разряжения в звуковой волне являются адиабатическими. Это связано с тем, что вследствие низкой теплопроводности воздуха и быстроты изменения давления и плотности при звуковых колебаниях тепловая энергия не успевает уйти из сжатого элемента газа за время сжатия ( Уравнение адиабатического процесса имеет вид:
где Если продифференцировать уравнение (2.5), получим:
Элемент газа в трубе между плоскостями x и x + dx имеет объем Sdx, а изменение его объема будет равно Постоянное давление – Р 0, а звуковое – p. Таким образом, уравнение адиабатического сжатия (разрежения) воздуха в звуковой волне имеет вид:
или
С учетом уравнения неразрывности (2.3) получаем:
Волновое уравнение для звуковых волн в воздухе. Скорость звука Комбинируя уравнение неразрывности (2.3), уравнение Эйлера (2.4) и уравнение состояния (2.6), получаем уравнение для смещения частиц в звуковой волне
или
Если обозначить
Таким образом, для ξ мы получили волновое уравнение (см. раздел 1.2.4), которое описывает волну, распространяющуюся в воздухе со скоростью, равной
Величина с называется скоростью звука. При нормальных условиях плотность воздуха ρ 0 = 1,29 кг/м2, атмосферное давление Р 0 = 1,013·105 Па, и скорость звука в воздухе с = 330 м/с. При комнатной температуре (t = 180C) с = 340 м/с. Аналогичные (2.8) волновые уравнения можно записать для звукового давления, акустических добавок к плотности и температуре. Волны смещения, звукового давления, плотности и температуры распространяются с одинаковой скоростью. Эти волны связаны между собой, так как
Таким образом, если известно уравнение одной из этих волн, например: Величина ρ0 с называется волновым сопротивлением среды. При нормальных условиях
Плоская гармоническая звуковая волна
Решением волнового уравнения:
является функция вида:
Если волна гармоническая, то
где
Скорость колебаний частиц в волне:
где Звуковое давление:
где Отметим, что отношение звукового давления к колебательной скорости равно волновому сопротивлению среды Акустическая добавка к плотности равна:
где Акустическая добавка к температуре:
Следует отметить, что обычно задаются не амплитудные значения величин, характеризующих звуковые колебательные процессы в среде, а действующие или эффективные, которые при гармонических колебаниях в
Далее индекс e будем опускать и подразумевать, что если задается какая-то конкретная величина (
|
|||||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 760; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.234.50 (0.008 с.) |


 . (2.1)
. (2.1)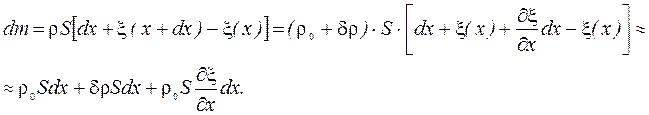 (2.2)
(2.2) .
. . (2.3)
. (2.3) .
.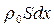 , а ускорение -
, а ускорение -  .
.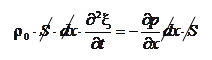
 . (2.4)
. (2.4) ).
). , (2.5)
, (2.5) - коэффициент Пуассона. Для воздуха
- коэффициент Пуассона. Для воздуха  .
. .
.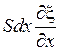 .
.
 . (2.6)
. (2.6) (2.7)
(2.7) :
:
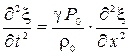
 , то
, то (2.8)
(2.8) .
. ,
, ,
, .
. , то остальные величины легко находятся.
, то остальные величины легко находятся. .
.
 .
. ,
,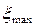 - амплитуда смещения частиц в волне;
- амплитуда смещения частиц в волне; - циклическая частота колебаний в волне;
- циклическая частота колебаний в волне; - волновое число;
- волновое число;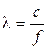 - длина звуковой волны.
- длина звуковой волны. ,
, - амплитуда колебательной скорости.
- амплитуда колебательной скорости.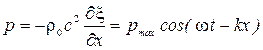 ,
,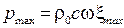 - амплитуда звукового давления.
- амплитуда звукового давления. .
.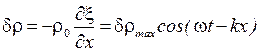 ,
,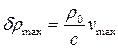 - амплитуда акустической добавки к плотности.
- амплитуда акустической добавки к плотности. .
. раз меньше амплитудных. Например:
раз меньше амплитудных. Например: .
. и так далее), то имеется в виду ее эффективное значение.
и так далее), то имеется в виду ее эффективное значение.


