
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Несобственный интеграл первого рода.Определённый интеграл. Определенный интеграл обозначается символом Формула Ньютона Лейбница Свойства:
Несобственный интеграл первого рода.
Обозначение
Определение Предположим, что функция
Если эта функция имеет предел при
а сам определенный интеграл называется сходящимся. Если же предела не существует, то интеграл называется расходящимся и не имеет никакого числового значения. Критерий Коши. Если функция
Несобственный интеграл второго рода. Обозначение
Пусть на полуинтервале
она определена при
Определение. Пусть функция
значение которого равняется левостороннему пределу
Если этот предел существует, то несобственный интеграл называется сходящимся, а если предела не существует, то расходящимся. Расходящемуся интегралу не приписывается никакого числового значения. Двойной интеграл. Двойной интеграл в декартовых координатах. Пусть функция Разобьём область D произвольным образом на элементарные ячейки Если существует предел последовательности интегральных сумм Вычисление двойного интеграла сводится к вычислению двукратных (повторных) интегралов. Пусть область D ограничена кривыми
Рис. 7 Если на отрезке
Рис. 8 В том случае, когда область D ограничена кривыми
Рис. 9 Если область D правильна в направлении обеих координатных осей, то двойной интеграл по такой области можно вычислять в любом порядке, то есть
Двойной интеграл в полярных координатах. Пусть область D ограничена линией Замечание. Если область D в декартовых координатах задаётся уравнением, содержащим бином x2+y2, например, x2+y2=R2, x2+y2=x,
Рис. 11 x2+y2=x2-y2 и т.д., то вычисление двойного интеграла по такой области удобнее производить в полярных координатах.
Определение Пусть кривая C описывается векторной функцией Если на кривой C определена скалярная функция F, то интеграл
Криволинейный интеграл
Определение Предположим, что кривая C задана векторной функцией
представляет собой единичный вектор, направленный вдоль касательной к данной кривой (рисунок 1). В приведенной выше формуле α, β и γ − углы между касательной и положительными направлениями осейO x, O y и O z, соответственно.
Введем векторную функцию
существовал криволинейный интеграл
Таким образом, по определению,
где Последнюю формулу можно переписать также в векторной форме:
где Если кривая C лежит в плоскости O xy, то полагая R = 0, получаем
Тройной интеграл.
Если существует такой предел, который не зависит от способа разбиения области и от выбора точки
Свойства. 1) V=V1ÈV2ÈV3È…ÈVn;
2) Теорема о среднем.
Определённый интеграл. Определенный интеграл обозначается символом Формула Ньютона Лейбница Свойства:
Несобственный интеграл первого рода.
Обозначение
Определение Предположим, что функция
Если эта функция имеет предел при
а сам определенный интеграл называется сходящимся. Если же предела не существует, то интеграл называется расходящимся и не имеет никакого числового значения. Критерий Коши. Если функция
|
||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 390; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.006 с.) |





 задана на бесконечном промежутке вида
задана на бесконечном промежутке вида 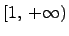 и интегрируема на любом конечном отрезке
и интегрируема на любом конечном отрезке  , где
, где  . Таким образом, можно рассмотреть функцию, зависящую от верхнего предела, как от переменной:
. Таким образом, можно рассмотреть функцию, зависящую от верхнего предела, как от переменной:
 , то число
, то число 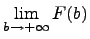 называется значением несобственного интеграла первого рода:
называется значением несобственного интеграла первого рода: интегрируема на отрезке
интегрируема на отрезке  >
>  , то для сходимости несобственного интеграла
, то для сходимости несобственного интеграла  необходимо и достаточно, чтобы для любого сколь угодно малого положительного числа
необходимо и достаточно, чтобы для любого сколь угодно малого положительного числа  >0 существовало число
>0 существовало число  такое, что для любых двух чисел
такое, что для любых двух чисел  >
> 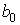 и
и 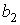 >
>  <
< 

 задана функция
задана функция  эта функция может быть вовсе не определена и стремиться к
эта функция может быть вовсе не определена и стремиться к  , либо вовсе не иметь никакого предела. Рассмотрим функцию
, либо вовсе не иметь никакого предела. Рассмотрим функцию
 . Эта функция может иметь предел при
. Эта функция может иметь предел при  (левосторонний предел). Этот предел будем называть значением интеграла от
(левосторонний предел). Этот предел будем называть значением интеграла от 

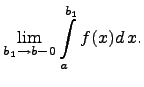
 определена и непрерывна в замкнутой ограниченной области D плоскости 0xy.
определена и непрерывна в замкнутой ограниченной области D плоскости 0xy. , в каждой из которых зафиксируем точку
, в каждой из которых зафиксируем точку  . Составим сумму
. Составим сумму  , называемую интегральной, которая соответствует данному разбиению D на части и данному выбору точек
, называемую интегральной, которая соответствует данному разбиению D на части и данному выбору точек  .
. при
при  –диаметр ячеек
–диаметр ячеек  и этот предел не зависит ни от способа разбиения области D на элементарные ячейки, ни от выбора точек
и этот предел не зависит ни от способа разбиения области D на элементарные ячейки, ни от выбора точек  , то он называется двойным интегралом от функции f(x,y) по области D и обозначается
, то он называется двойным интегралом от функции f(x,y) по области D и обозначается  .
. ,
,  ,
,  ,
,  , причем
, причем 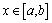 , а функции
, а функции  непрерывны на отрезке
непрерывны на отрезке  . Прямая, параллельная оси 0y, пересекает границу области D не более чем в двух точках. Такую область D называют простой и правильной в направлении оси 0y. Тогда
. Прямая, параллельная оси 0y, пересекает границу области D не более чем в двух точках. Такую область D называют простой и правильной в направлении оси 0y. Тогда 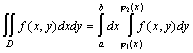 , причём сначала вычисляется внутренний интеграл по переменной y, а полученный результат интегрируем по x.
, причём сначала вычисляется внутренний интеграл по переменной y, а полученный результат интегрируем по x.

 ,
,  , непрерывными на
, непрерывными на  , прямыми
, прямыми  и
и  , область D является простой и правильной в направлении оси 0x. Двойной интеграл по такой области вычисляют по формуле:
, область D является простой и правильной в направлении оси 0x. Двойной интеграл по такой области вычисляют по формуле:  .
.
 .
.
 и лучами
и лучами  и
и  , где
, где  и
и  – полярные координаты точки на плоскости, связанные с её декартовыми координатами x и y соотношениями
– полярные координаты точки на плоскости, связанные с её декартовыми координатами x и y соотношениями  ,
,  . В этом случае
. В этом случае 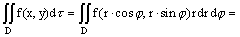
 .
.
 , где переменная s представляет собой длину дуги кривой (рисунок 1).
, где переменная s представляет собой длину дуги кривой (рисунок 1). называется криволинейным интегралом первого рода от скалярной функции F вдоль кривой C и обозначается как
называется криволинейным интегралом первого рода от скалярной функции F вдоль кривой C и обозначается как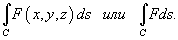
 существует, если функция F непрерывна на кривой C.
существует, если функция F непрерывна на кривой C.




 , определенную на кривой C, так, чтобы для скалярной функции
, определенную на кривой C, так, чтобы для скалярной функции
 . Такой интеграл
. Такой интеграл  вдоль кривой C и обозначается как
вдоль кривой C и обозначается как

 − единичный вектор касательной к кривой C.
− единичный вектор касательной к кривой C.
 .
.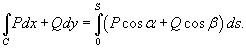
 3,
3, 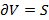 ,
,  ,
, 
 iÎVi,
iÎVi,  i
i  i =
i = 
 Вычисление.
Вычисление.





