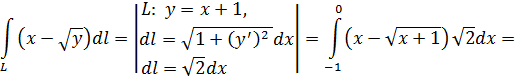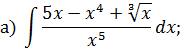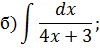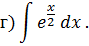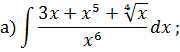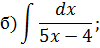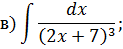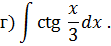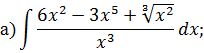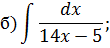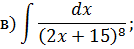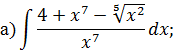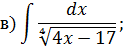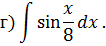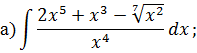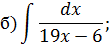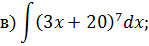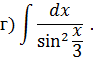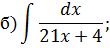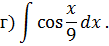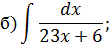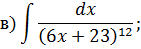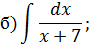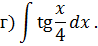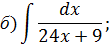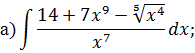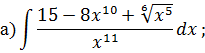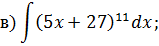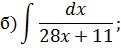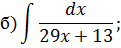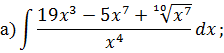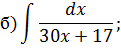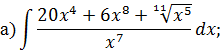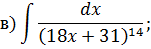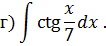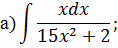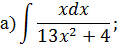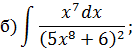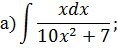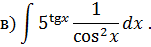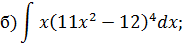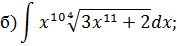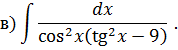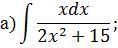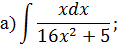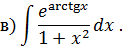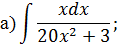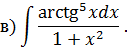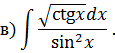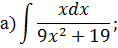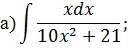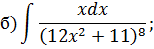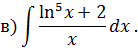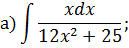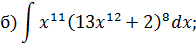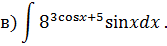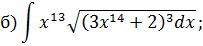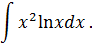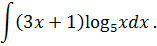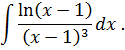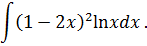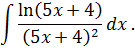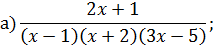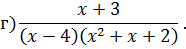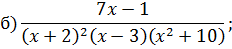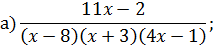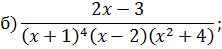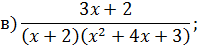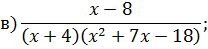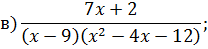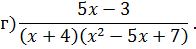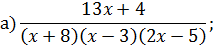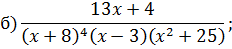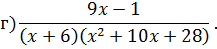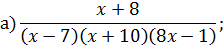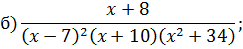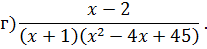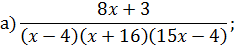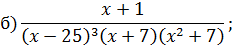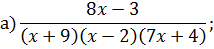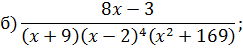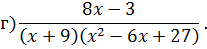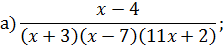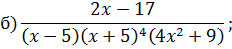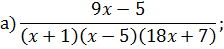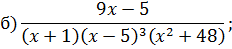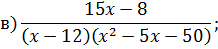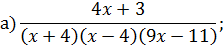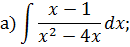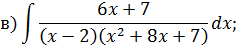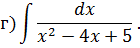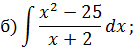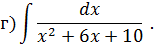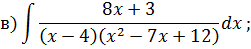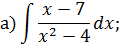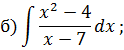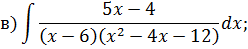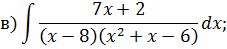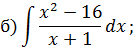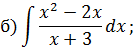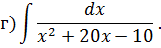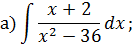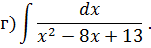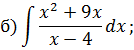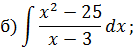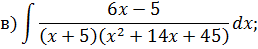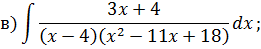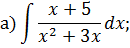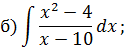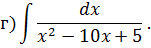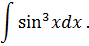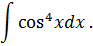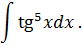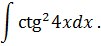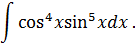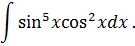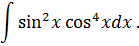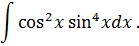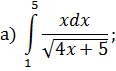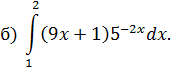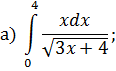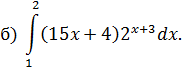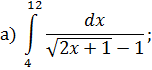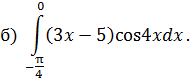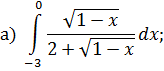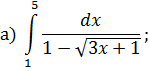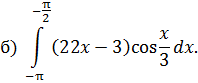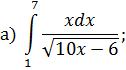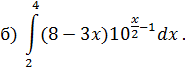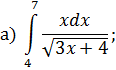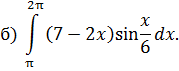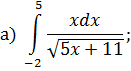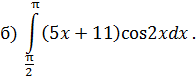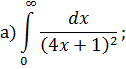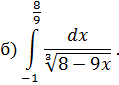Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Криволинейный интеграл по координатамСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Задача 14. Вычислить криволинейный интеграл
2) L: дуга параболы 3) L: ломаная АСВ, где А(0;0), С(1;0), В(1;2). Решение. Для вычисления криволинейного интеграла по координатам надо с помощью заданного пути интегрирования преобразовать криволинейный интеграл в определенный интеграл. Пределы интегрирования зависят от того к какой переменной осуществляется переход под знаком интеграла.
в) В данном случае путь интегрирования – ломаная АСВ, где А(0;0), С(1;0), В(1;2) (рис.5).
Рис. 5 Ломаная АСВ состоит из двух звеньев АС и СВ. Поэтому исходный интеграл по ломаной АСВ следует разбить на сумму двух интегралов по путям АС и СВ.
Криволинейный интеграл по длине дуги Задача 15. Вычислить криволинейный интеграл по длине дуги Решение.
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ Задача 1. Табличное интегрирование.
Задача 2. Используя метод замены переменной, найдите интегралы:
Задача 3. Используя метод интегрирования по частям, найдите интегралы:
Задача 4. Разложить дробь на простейшие, используя метод неопределенных коэффициентов.
Задача 5. Найдите интегралы от рациональных функций:
Задача 6. Найти интегралы от тригонометрических функций:
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ Задача 7. Вычислить интегралы:
Задача 8. Вычислить несобственные интегралы:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 2532; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.227.187 (0.012 с.) |


 от т.А(0;0) до т.В(1;2);
от т.А(0;0) до т.В(1;2); от т.А(2;1) до т.В(8;2);
от т.А(2;1) до т.В(8;2);

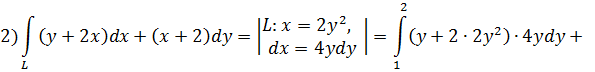

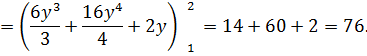




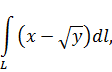
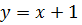 от точки
от точки  до точки
до точки 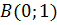 .
.