
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства определенного интеграла.Содержание книги
Поиск на нашем сайте
1. 2. 3. 4. 5. Свойства Ньютона – Лейбница. Если функция f (х) непрерывна на сегменте Основные методы интегрирования определенного интеграла: Метод непосредственного интегрирования – это метод нахождения определенного интеграла на основе свойств, таблицы основных интегралов, формулы Ньютона-Лейбница. Замена переменной интегрирования производится по следующей формуле:
Метод внесения под знак дифференциала работает по формуле:
Метод интегрирования по частям работает по формуле: Геометрические приложения определенного интеграла. Площадь криволинейной трапеции. Пусть функция f (х) непрерывна на сегменте Площадь в полярных координатах. Пусть требуется определить площадь сектора, ограниченного лучами
Длина дуги кривой. Пусть функция f (х) непрерывна на сегменте РАЗДЕЛ «Численные методы» Абсолютная погрешность. Абсолютной погрешностью Граница абсолютной погрешности. Границей абсолютной погрешности приближения Относительная погрешность. Относительной погрешностью Граница относительной погрешности. Границей относительной погрешности приближения Приближенное числовое значение функции. Приближенное числовое значение функции можно найти с помощью дифференциала по формуле Приближенное вычисление определенного интеграла. Приближенное вычисление определенного интеграла от функции Приближенное решение уравнения. Приближенным решением уравнения Метод хорд нахождения корней уравнения Метод касательных (метод Ньютона) нахождения корней уравнения Интерполяционный многочлен Лагранжа. Пусть дана таблица
РАЗДЕЛ «Ряды» Числовой ряд. Числовым рядом называется выражение Число Частичная сумма ряда. Сумма первых n членов числового ряда - sn = Сходимость числового ряда. Если существует предел последовательности частичных сумм Знакочередующийся ряд. Знакочередующимся рядом называется ряд вида:
Абсолютная сходимость ряда. Ряд Степенной ряд. Степенным рядом называется ряд вида
где an Î R называются коэффициентами ряда, x Î R. Радиус сходимости. Радиусом сходимости степенного ряда 1) на интервале (- R, R) ряд сходится, 2) если | x | > R, то ряд расходится. Интервал (- R, R) называется интервалом сходимости (не исключается случай R = +¥). Разложение функции в ряд. Функция f (x) раскладывается в степенной ряд на интервале (x 0 - R, x 0 + R), если существует степенной ряд Ряд Тейлора. Степенной ряд Теорема 1 (признак сравнения рядов). Пусть даны два поло-жительных числовых ряда Теорема 2. Положительный числовой ряд, Теорема 3 (признак Даламбера). Если члены положительного числового ряда Теорема 4 (признак Коши). Если члены положительного числового ряда Теорема 5 (признак Лейбница). Если члены знакочередующегося ряда Теорема 6. Пусть для степенного ряда
|
||||
|
Последнее изменение этой страницы: 2016-12-28; просмотров: 153; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.25.117 (0.009 с.) |

 ;
;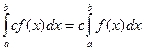 ;
; ;
; ;
; , где
, где 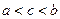 .
. и
и  - первообразная функции f (х) на этом отрезке, то
- первообразная функции f (х) на этом отрезке, то  =
=  -
-  .
. , где
, где 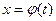 и функция
и функция  имеет непрерывную производную,
имеет непрерывную производную, 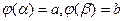 .
. = =
= = 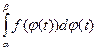 .
.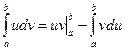 ,
,  и
и  - дифференцируемые функции на сегменте
- дифференцируемые функции на сегменте  криволинейной трапеции, ограниченной линиями y = f (х), y = 0, х = а, х=
криволинейной трапеции, ограниченной линиями y = f (х), y = 0, х = а, х=  , равна интегралу
, равна интегралу  . Пусть функции f1 (х), f2 (х) непрерывны на сегменте
. Пусть функции f1 (х), f2 (х) непрерывны на сегменте  .
. и кривой
и кривой 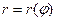 , где
, где  - непрерывна на сегменте
- непрерывна на сегменте 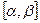 , тогда
, тогда .
. заданной функцией y = f (х) и ограниченной х = а, х=
заданной функцией y = f (х) и ограниченной х = а, х= 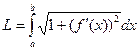 .
.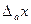 приближения
приближения  называется модуль разности
называется модуль разности 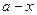 , т.е.
, т.е. 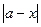 .
. , которое больше (или равно) абсолютной погрешности
, которое больше (или равно) абсолютной погрешности 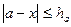 .
.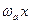 приближенного числа
приближенного числа  называется отношение абсолютной погрешности этого числа к модулю точного значения
называется отношение абсолютной погрешности этого числа к модулю точного значения 
 данной величины, т.е.
данной величины, т.е.  .
. , которое больше (или равно) относительной погрешности
, которое больше (или равно) относительной погрешности  .
. .
. на
на  и
и 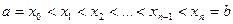 , при разбиении отрезка на n равных интервалов, длина интервала
, при разбиении отрезка на n равных интервалов, длина интервала  , значения функции:
, значения функции: 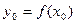 ,
,  , …,
, …,  , тогда по формуле прямоугольников:
, тогда по формуле прямоугольников:  , а по формуле трапеций:
, а по формуле трапеций: 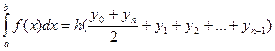 .
.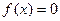 называется такое приближенное значение корня, что образованная последовательность приближенных корней стремится к точному значению корня.
называется такое приближенное значение корня, что образованная последовательность приближенных корней стремится к точному значению корня.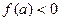 и
и  (
( и
и 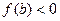 ), тогда первое приближение
), тогда первое приближение 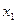 найдем по формуле
найдем по формуле  , если
, если  и
и 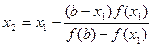 и далее последовательность
и далее последовательность  стремится к корню при заданной точности вычисления.
стремится к корню при заданной точности вычисления.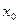 такую, что
такую, что  и
и  - одного знака, тогда первое приближение
- одного знака, тогда первое приближение  , и т. д. последовательность
, и т. д. последовательность  стремится к корню при заданной точности вычисления.
стремится к корню при заданной точности вычисления.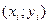 , где
, где  , требуется составить функцию
, требуется составить функцию  -многочлен степени
-многочлен степени 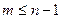 которая принимала бы заданные значения
которая принимала бы заданные значения  при соответствующих
при соответствующих  , т.е.
, т.е.  , т.е. график этого многочлена проходит через точки
, т.е. график этого многочлена проходит через точки  . Обозначим через
. Обозначим через  вспомогательный многочлен. Тогда
вспомогательный многочлен. Тогда  +
+  +…+
+…+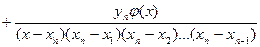 - интерполяционный многочлен Лагранжа.
- интерполяционный многочлен Лагранжа.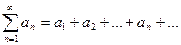
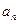 называется общим членом ряда (
называется общим членом ряда ( .
. называется частичной суммой ряда.
называется частичной суммой ряда.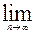 sn = s, то числовой ряд называется сходящимся, а число s называется суммой ряда
sn = s, то числовой ряд называется сходящимся, а число s называется суммой ряда  Если
Если  , то ряд называется расходящимся.
, то ряд называется расходящимся. где
где  .
.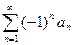 называется абсолютно сходящимся, если сходится ряд
называется абсолютно сходящимся, если сходится ряд  . Ряд
. Ряд 
 называется число R ³ 0 обладающее свойствами:
называется число R ³ 0 обладающее свойствами: сходящийся к f (x) на этом интервале, т.е. если
сходящийся к f (x) на этом интервале, т.е. если 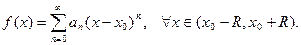
 называется рядом Тейлора функции f (x) в точке x 0, f(n) (x0) – значение производной n - порядка в точке x 0.
называется рядом Тейлора функции f (x) в точке x 0, f(n) (x0) – значение производной n - порядка в точке x 0. и
и  , если члены ряда
, если члены ряда  , т.е.
, т.е. 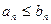
 , то из сходимости ряда
, то из сходимости ряда 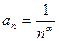 , сходится тогда и только тогда, когда
, сходится тогда и только тогда, когда  , в противном случае ряд расходится.
, в противном случае ряд расходится.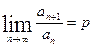 , то при
, то при  ряд сходится, при
ряд сходится, при 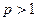 ряд расходится, при
ряд расходится, при 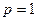 - ряд может, как сходиться, так и расходиться.
- ряд может, как сходиться, так и расходиться. , то при
, то при 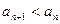
 , то ряд сходится.
, то ряд сходится. или
или  , тогда радиус сходимости степенного ряда
, тогда радиус сходимости степенного ряда  .
.


