
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Раздел «дифференциальное и интегральное исчисление функции одной переменной»Содержание книги
Поиск на нашем сайте Полином Тейлора. Многочлен вида: называется полиномом Тейлора функции f (х) в точке х 0. Возрастающая и убывающая функция. Функция f (х) называется возрастающей (убывающей) в интервале (a, b), если для любых точек x 1, x 2 из (a, b), из неравенства Точка максимума, минимума. Пусть f (х) дифференцируема на (a, b). Если при переходе через точку х 0 из (a, b), функция f (х) меняет возрастание на убывание (убывание на возрастание), то х 0 называется точкой максимума (минимума) функции f (х). Выпуклость графика функции. Функция f (х) называется выпуклой вверх (вниз) на интервале (a, b), если для любых точек x 1, x 2 из (a, b), её график над интервалом (x 1, x 2) лежит выше (ниже) секущей – прямой, проходящей через точки (x 1, f (x 1)) и (x 2, f (x 2)). Точка перегиба. Пусть f (х) дифференцируема на (a, b). Если при переходе через точку х 0 из (a, b), функция f (х) меняет направление выпуклости, то х 0 называется точкой перегиба функции f (х). Асимптота. Прямая х = х 0 называется вертикальной асимптотой графика функции y = f (х), если хотя бы один из односторонних пределов в точке х 0 равен +¥ или –¥. Прямая y = kх + b называется наклонной асимптотой графика y = f (х) при x →±
Теорема 1. Если функция y = f (х), дифференцируемая в интервале (a, b), неубывающей (невозрастающей) на нем, то ее производная в этом интервале не отрицательна (не положительна), т.е. Теорема 2. Если функция y = f (х), дифференцируемая в интервале (a, b), удовлетворяет в нем условию Теорема 3. (необходимое условие существования экстремума) Если функция y = f (х), дифференцируемая в интервале (a, b), имеет в точке Теорема 4. (достаточное условие существования экстремума) Если производная функции y = f (х) обращается в точке Теорема 5. Если вторая производная Теорема 7. (правило Лопиталя)Предел отношения двух бесконечно малых или бесконечно больших функций равен пределу отношения их производных, если последний существует, т.е. Первообразная. Функция F(x) называется первообразной для данной функции f (х) на данном промежутке, если на этом промежутке Определенный интеграл. Выражение Свойства неопределенного интеграла. 1. 2. 3. 4. Основные методы интегрирования. Метод непосредственного интегрирования – это метод нахождения неопределенного интеграла на основе свойств и таблицы основных интегралов. Замена переменной интегрирования производится по следующей формуле:
Метод внесения под знак дифференциала работает по формуле: Метод интегрирования по частям работает по формуле: Определенный интеграл. Если существует предел
|
||
|
Последнее изменение этой страницы: 2016-12-28; просмотров: 195; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |


 вытекает неравенство
вытекает неравенство  (соответственно
(соответственно  ). Если же для любых точек x 1, x 2 из (a, b), из неравенства
). Если же для любых точек x 1, x 2 из (a, b), из неравенства 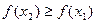 (соответственно
(соответственно  ), то функция f (х) называется неубывающей (невозрастающей) на интервале (a, b).
), то функция f (х) называется неубывающей (невозрастающей) на интервале (a, b). , если
, если (f (х) - (kх + b)) = 0.
(f (х) - (kх + b)) = 0. (
( ).
). (
( ), то эта функция возрастает (убывает) в интервале (a, b).
), то эта функция возрастает (убывает) в интервале (a, b).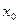 ,
,  , экстремум, то ее производная в этой точке равна нулю:
, экстремум, то ее производная в этой точке равна нулю:  .
. меняет знак плюс (минус) на минус (плюс), то в точке
меняет знак плюс (минус) на минус (плюс), то в точке  функции y = f (х) положительна (отрицательна) в интервале (a, b), то график этой функции является выпуклым вниз (вверх) в интервале (a, b). Теорема 6. Если вторая производная
функции y = f (х) положительна (отрицательна) в интервале (a, b), то график этой функции является выпуклым вниз (вверх) в интервале (a, b). Теорема 6. Если вторая производная  .
. .
.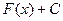 , где
, где  - первообразная функции f (х) и обозначается символом
- первообразная функции f (х) и обозначается символом  , причем f (х) называется подынтегральной функцией,
, причем f (х) называется подынтегральной функцией,  - подынтегральным выражением,
- подынтегральным выражением,  - знаком интеграла. Таким образом, по определению,
- знаком интеграла. Таким образом, по определению,  или
или  ;
; или
или  ;
; ;
; =
=  +
+ 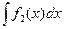 .
.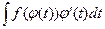 , где
, где 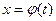 и функция
и функция  имеет непрерывную производную.
имеет непрерывную производную. =
=  = =
= =  .
.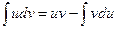 ,
,  и
и  - дифференцируемые функции.
- дифференцируемые функции. , не зависящий от способа разбиения отрезка
, не зависящий от способа разбиения отрезка  и выбора точек
и выбора точек  , то этот предел будем называть определенным интегралом функции f (х) на сегменте
, то этот предел будем называть определенным интегралом функции f (х) на сегменте  =
= 


