
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
РАЗДЕЛ «Дифференциальные уравнения»Содержание книги
Поиск на нашем сайте
Дифференциальное уравнение. Дифференциальным уравнением называется соотношение, связывающее независимую переменную х искомую функцию Порядок дифференциального уравнения. Порядок старшей производной, входящей в дифференциальное уравнение, называется порядком дифференциального уравнения. Решение дифференциального уравнения. Всякая функция Дифференциальное уравнение первого порядка. Дифференциальным уравнением первого порядка называется соотношение, связывающее независимую переменную х искомую функцию Общее решение дифференциального уравнения первого порядка. Решение уравнения Дифференциальное уравнение с разделяющимися переменными первого порядка. Дифференциальным уравнением первого порядка с разделяющимися переменными называется уравнение вида Дифференциальное уравнение с разделенными переменными первого порядка. Дифференциальным уравнением первого порядка с разделенными переменными называется уравнение вида Однородная функция. Функция Однородное дифференциальное уравнение первого порядка. Однородным дифференциальным уравнением первого порядка называется уравнение вида Линейные дифференциальные уравнения первого порядка. Линейным дифференциальным уравнением первого порядка называется уравнение вида Уравнение Бернулли. Дифференциальное уравнение первого порядка называется уравнением Бернулли, если оно имеет вид Дифференциальное уравнение второго порядка. Дифференциальным уравнением второго порядка называется соотношение, связывающее независимую переменную х искомую функцию Общее решение дифференциального уравнения второго порядка. Решение уравнения Линейные дифференциальные уравнения второго порядка. Линейным дифференциальным уравнением второго порядка называется уравнение вида Линейные однородные уравнения второго порядка с постоянными коэффициентами. Линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами называется уравнение вида Линейные неоднородные уравнения второго порядка с постоянными коэффициентами. Линейным неоднородным дифференциальным уравнением второго порядка с постоянными коэффициентами называется уравнение вида Теорема 1. Если Теорема 2. Общее решение линейного неоднородного дифференциального уравнения второго порядка
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-28; просмотров: 154; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.14.210 (0.008 с.) |

 и ее производные
и ее производные  .
. .
. называется общим решением уравнения.
называется общим решением уравнения. .
. .
. называется однородной степени
называется однородной степени  , если имеет место тождество
, если имеет место тождество 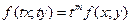 .
. , если функции
, если функции  являются однородными функциями одной и той же степени.
являются однородными функциями одной и той же степени.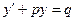 , где
, где  - непрерывная функция на
- непрерывная функция на  .
.  , где
, где  .
. и имеющее вид
и имеющее вид 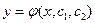 называется общим решением уравнения.
называется общим решением уравнения. , где
, где 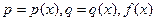 - непрерывные функции на
- непрерывные функции на  , где
, где 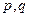 - постоянные действительные числа.
- постоянные действительные числа.  - непрерывная функция на
- непрерывная функция на  - линейные независимые частные решения линейного однородного дифференциального уравнения второго порядка
- линейные независимые частные решения линейного однородного дифференциального уравнения второго порядка  - непрерывные функции на
- непрерывные функции на  , где
, где  - постоянные.
- постоянные. , где
, где 


