Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Первообразная и неопределенный интегралСодержание книги
Поиск на нашем сайте
Первообразная и неопределенный интеграл Функция F(x), дифференцируемая на X, называется первообразной для функции f(x), если всюду на этом промежутке выполняется равенство: F’(x)=f(x). Если F(x) – первообразная для f(x), то первообразной для f(x) так же будет являться функция F(x)+C, C=const. Имеет место и обратное утверждение: любые 2 первообразные функции f(x) отличаются друг от друга на постоянную. Совокупность всех первообразных для f(x) называется неопределенным интегралом и обозначается: ∫f(x)dx. Свойства неопределенного интеграла: 1. ∫ (f(x)dx)’=f(x) 2. ∫ F’(x)dx=F(x)+C 3. ∫ (f(x)+g(x))dx=∫ f(x)dx+∫ g(x)dx 4. ∫ K*f(x)dx= K∫ f(x)dx
Основные методы интегрирования Замена переменных: пусть требуется вычислить интеграл ∫ f(x)dx и мы нашли функцию x=x(t), которая на промежутке дифференцируемая, монотонна, непрерывна и существует обратная функция t=t(x) и интеграл превратится в следующий: ∫ f(x)dx= ∫ f(x)*x’(t)dt= F(t)+C= F(t(x))+C Интегрирование по частям: пусть u(x) и v(x) – две непрерывные дифференцируемые функции, тогда имеет место формула: ∫ udv= uv-∫vdu или ∫u v’dx= u*v - ∫ v*u’dx Интегрирование рациональный дробей: (a0+a1x+…+amxm)/(b0+b1x+…+bnxn)= Pm(x)/an(x), причем если m>n, то дробь неправильная, если m<=n, то дробь правильная
Интегрирование тригонометрических выражений 1) Интегралы вида ∫ sinKx*sinMx dx, ∫sin Kx*cos Mx dx, ∫ cos Kx*cos Mx dx вычисляются преобразованием произведения тригонометрических функций в сумму по формулам: Sin Kx*sin Mx=1/2(cos(k-m)x-cos(k+m)x) Sin Kx*cos Mx=1/2(sin(k-m)x+sin(k+m)x) Cos Kx*cos Mx=1/2 (cos(k-m)x+cos(k+m)x) 2) Интегралы вида ∫ cosmx*sinnx dx, где m или n – нечетное положительное число, вычисляются подведением под знак дифференциала. 3)) Интегралы вида ∫ cosmx*sinnx dx, где m или n – четное положительное число, вычисляются с помощью формул понижения степени: Sin2α=1/2(1-cos2α); cos2α=1/2(1+cos2α); sinα*cosα=1/2sin2α 4) Интегралы вида ∫ tgmx dx, ∫ctgmx dx, где m принадлежит N, вычисляются заменой переменной tgx=z, x=arctgz, dx=dz/1+z2 или ctgx=z, x=arcctgz, dx= -dz/1+z2 5) Интегралы вида ∫ R(sinx,cosx)dx сводятся к интегралам от рациональных дробей с помощью универсальной подстановки tg x/2=z, тогда x=2arctgz, dx=2dz/1+z2, sinx=2z/1+z2, cosx=(1-z2)/(1+z2)
Интегрирование простейших иррациональных. Существуют 2 метода интегрирования иррациональных выражений: метод подстановки, метод интегрирования по частям. Способ рационализации иррациональных выражений заключается в том, что мы подбираем такую замену, чтобы наша иррациональная дробь стала рациональной. Интегралы простейших иррациональных дробей:
Этот интеграл выражается через элементарные функции, т.к. подинтегральная функция всегда рационализируется следующей заменой:
Интегрирование дробно-рациональных функций Функция вида P(x)/Q(x), где P(x),Q(x) – многочлены, называется дробно-рациональной функцией. Обычно, дробно рациональные функции интегрируются с помощью разложения на простейшие дроби.
Определенный интеграл Римана Функция f(x) называется интегрированной по Риману на [a;b], если существует конечный предел Обозначаемый интеграл всегда число и не зависит от переменной интегрирования. Если функция интегрируема на отрезке [a;b], то она ограничена
Приложения определенного интеграла 1) Вычисление S плоских фигур Пусть f(x)>=0 на [a;b] и непрерывна на нем. Вычисление S криволинейной трапеции= 2) Вычисление объемов тел
Если кривая задана параметрически и u’>0, то
3) Вычисление длины дуги кривой
Если кривая задана параметрически, то Если дуга задана уравнением q=q(u), то 4) Вычисление площади поверхности вращения
Дифференциальные уравнения. Основные понятия Дифференциальные уравнения – это одно или несколько уравнений с производными некоторых функций. Порядком дифференциального уравнения называется порядок наивысшей производной, входящей в это уравнение. Общий вид дифференциального уравнения n-го порядка: F(x,y,y’,y’’,…,y(n))=0 Общим решением дифференциального уравнения называется функция y=f(x), зависящая от х и произвольных постоянных, при подстановке которых дифференциальное уравнение обращается в тождество. Если решение ДУ задается в виде уравнения, не разрешенного относительно у, то его называют общим интегралом.
Степенные ряды Степенным называется функциональный ряд вида а0+а1х+а2х2+…+аnxn+…= Теорема Абеля: если ряд (1) сходится в т.х0, то он сходится абсолютно для всех х, таких что 0≤|x|≤|x0| О радиусе сходимости: пусть ряд (1) сходится не только при х0, но и не на всей числовой прямой, тогда существует положительное число R, такое что для всех х принадлежащем интервалу от –R до R ряд сходится, и для всех х не принадлежащих отрезку от –R до R расходится, число R называется радиусом сходимости степенного ряда. Радиус сходимости степенного ряда может быть вычислен по формулам: 1) 2) если существует предел Свойства: 1) Степенной ряд внутри интервала сходимости сходится равномерно 2) Суммой степенного ряда является функция, непрерывная внутри интервала сходимости 3) Пусть внутри интервала от –R до R степенной ряд сходится, тогда, для любого отрезка от 0 до х, принадлежащему этому интервалу, степенной ряд можно почленно интегрировать
Применение рядов. Числовые функциональные ряды применяются в приближенных вычислениях: 1) при решении дифференциальных уравнений 2) при приближенном вычислении интегралов Вычисление значений функции с помощью рядов: пусть необходимо вычислить значение функции f(x) в т.х0=х заданной точностью
Взяв достаточное количество членов, получим приближенное равенство, точность которого увеличивается с членом n. Первообразная и неопределенный интеграл Функция F(x), дифференцируемая на X, называется первообразной для функции f(x), если всюду на этом промежутке выполняется равенство: F’(x)=f(x). Если F(x) – первообразная для f(x), то первообразной для f(x) так же будет являться функция F(x)+C, C=const. Имеет место и обратное утверждение: любые 2 первообразные функции f(x) отличаются друг от друга на постоянную. Совокупность всех первообразных для f(x) называется неопределенным интегралом и обозначается: ∫f(x)dx. Свойства неопределенного интеграла: 1. ∫ (f(x)dx)’=f(x) 2. ∫ F’(x)dx=F(x)+C 3. ∫ (f(x)+g(x))dx=∫ f(x)dx+∫ g(x)dx 4. ∫ K*f(x)dx= K∫ f(x)dx
|
||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 300; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.162.166 (0.01 с.) |

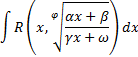

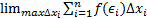 , называемый определенным интегралом Римана. Обозначается:
, называемый определенным интегралом Римана. Обозначается: 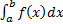
 . Если же фигура ограничена функциями f(x) – сверху, g(x) – снизу, то
. Если же фигура ограничена функциями f(x) – сверху, g(x) – снизу, то 
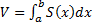 , где S(x) – площадь сечения,
, где S(x) – площадь сечения, 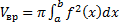

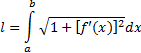



 (1)
(1)
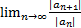 =D, то R=1/D
=D, то R=1/D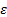 ; и пусть эта функция разлагается по степени (х-а) в интервале (a-R;a+R), х0 принадлежит этому интервалу.
; и пусть эта функция разлагается по степени (х-а) в интервале (a-R;a+R), х0 принадлежит этому интервалу. , тогда
, тогда