
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Первообразная и неопределенный интеграл.Содержание книги
Поиск на нашем сайте Первообразная и неопределенный интеграл. Понятие первообразной и неопределенный интеграл Определение. Функция Пример. Можно заметить, что если для функции Теорема. Если
Из данной теоремы следует, что, если Определение. Совокупность всех первообразных функции Таким образом:
где Определение. Операция нахождения неопределенного интеграла называется интегрированием этой функции. Свойства неопределенного интеграла 1) Производная от неопределенного интеграла равна подынтегральной функции, т.е. □ Доказательство. Дифференцируя левую и правую части равенства 2) Дифференциал неопределенного интеграла равен подынтегральному выражению, т.е. □ Доказательство. По определению дифференциала и свойству 1 имеем: 3) Неопределенный интеграл от дифференциала некоторой функции равен этой функции с точностью до постоянного слагаемого, т.е. □ Доказательство. Рассматривая функцию 4) Постоянный множитель можно выносить за знак интеграла, т.е. 5) Интеграл от алгебраической суммы двух функций равен такой же сумме интегралов от этих функций, т.е. Метод замены переменной, интегрирование по частям. Интегрирование - действие, обратное дифференцированию, то каждому правилу дифференцирования должно соответствовать некоторое правило интегрирования. Пусть Интегрируя обе части последнего равенства, получим:
Это и есть формула интегрирования по частям. Интегрирование по частям состоит в том, что подынтегральное выражение 1) при отыскании 2) при отыскании интеграла от Может оказаться, что эти два интегрирования легко осуществляются, тогда как заданный интеграл непосредственно найти трудно. Правило интегрирования по частям нередко позволяет довести интегрирование до конца. Интегральная сумма определенный интеграл, его геометрический смысл Пусть на отрезке
Обозначим через Определение. Определенным интегралом от функции
Замечание 1. Переменную под знаком интеграла можно обозначать любой буквой: Замечание 2. В отличие от неопределенного интеграла Геометрический смысл определенного интеграла.
Формула ньютона-лейбница Формула Ньютона-Лейбница. Теорема. Пусть функция
Значение определённого интеграла равно разности значений любой первообразной от подынтегральной функции, взятых при верхнем и нижнем пределах интеграла. Другими словами, Значение определённого интеграла равно приращению любой первообразной от подынтегральной функции на интервале интегрирования. Формула Ньютона-Лейбница позволяет находить определённый интеграл, обходя суммирование, при помощи первообразных функций.
Несобственные интегралы Частные производные Основные понятия. Частные производные Определение. Пусть имеется Переменные Функцию двух переменных будем обозначать как Определение. Графиком функции двух переменных Первообразная и неопределенный интеграл.
|
||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 417; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

 называется первообразной функцией для функции
называется первообразной функцией для функции  на промежутке
на промежутке  , если в каждой точке этого промежутка
, если в каждой точке этого промежутка  .
. является первообразной для
является первообразной для  , т.к.
, т.к.  .
. существует первообразная
существует первообразная  , то она не является единственной. Возвращаясь к примеру, видно, что и функции
, то она не является единственной. Возвращаясь к примеру, видно, что и функции  ,
,  и вообще
и вообще  (
( - некоторое число) являются первообразными для функции
- некоторое число) являются первообразными для функции  . Таким образом можно сформулировать следующую теорему.
. Таким образом можно сформулировать следующую теорему. и
и  - первообразные для функции
- первообразные для функции  .
. , где
, где  на промежутке
на промежутке  , где
, где  - знак интеграла,
- знак интеграла,  - подынтегральное выражение.
- подынтегральное выражение. ,
, - некоторая первообразная для
- некоторая первообразная для  .
. .■
.■ .
. ■
■ .
. , откуда
, откуда  .■
.■ , где
, где  - некоторое число.
- некоторое число. .
. и
и  - дифференцируемые функции от
- дифференцируемые функции от  х. Имеем:
х. Имеем:  , откуда
, откуда  .
. , или
, или .
. представляется каким-либо образом в виде произведения двух множителей
представляется каким-либо образом в виде произведения двух множителей  (последний обязательно содержит
(последний обязательно содержит  ) и согласно формуле данное интегрирование заменяется двумя:
) и согласно формуле данное интегрирование заменяется двумя: ;
; .
. задана функция
задана функция  (рис. 10.1).
(рис. 10.1).
 на
на 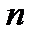 элементарных отрезков точками
элементарных отрезков точками  , где
, где  . На каждом отрезке разбиения выберем некоторую точку
. На каждом отрезке разбиения выберем некоторую точку  и положим
и положим  , где
, где  .
Сумму вида
.
Сумму вида  будем называть интегральной суммой для функции
будем называть интегральной суммой для функции  на отрезке
на отрезке  .
.
 максимальную из длин отрезков
максимальную из длин отрезков  , т.е.
, т.е.  .
. на отрезке
на отрезке  называется предел интегральной суммы при
называется предел интегральной суммы при  , т.е.
, т.е. . (10.1)
. (10.1) - нижний предел,
- нижний предел,  - верхний предел,
- верхний предел,  - подынтегральная функция,
- подынтегральная функция,  - подынтегральное выражение.
- подынтегральное выражение. и т. д.
и т. д. , который представляет семейство функций (первообразных), определенный интеграл
, который представляет семейство функций (первообразных), определенный интеграл  есть определенное число.
есть определенное число. Пусть на отрезке
Пусть на отрезке  криволинейной трапеции, ограниченной кривой
криволинейной трапеции, ограниченной кривой  , прямыми
, прямыми  ,
,  и осью абсцисс
и осью абсцисс  (рис.10.2) численно равна определенному интегралу от функции
(рис.10.2) численно равна определенному интегралу от функции 
 и
и  - любая первообразная для
- любая первообразная для  на
на  .
. переменных величин и каждому набору их значений
переменных величин и каждому набору их значений  из некоторого множества
из некоторого множества  соответствует одно вполне определенное значение переменной величины
соответствует одно вполне определенное значение переменной величины  из множества
из множества  . тогда говорят, что задана функция нескольких переменных
. тогда говорят, что задана функция нескольких переменных  .
. называются независимыми переменными или аргументами,
называются независимыми переменными или аргументами,  - зависимая переменная. Множество
- зависимая переменная. Множество  называется областью определения функции, множество
называется областью определения функции, множество  - областью значений функции.
- областью значений функции. .
. ), аппликата
), аппликата  которых связана с абсциссой
которых связана с абсциссой  и ординатой
и ординатой  функциональным соотношением
функциональным соотношением  . График представляет собой некоторую поверхность в трехмерном пространстве.
. График представляет собой некоторую поверхность в трехмерном пространстве.


