
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод замены переменной (метод подстановки).Содержание книги
Поиск на нашем сайте
Одним из основных методов интегрирования является метод замены переменной (или метод подстановки), описываемый формулой:
Пусть заданный интеграл □ Найдем производные по переменной Формула показывает, что переходя к новой переменной, достаточно выполнить замену переменной в подынтегральном выражении. Удачная замена переменной позволяет упростить исходный интеграл, свести его к табличному. Замечание. Новую переменную можно не выписывать явно, а производить преобразования функции под знаком дифференциала (путем введения постоянных и переменных под знак дифференциала). Теорема. Пусть □ Перепишем Алгоритм вычисления: 1) Делаем замену. 2) Дифференцируем замену 3) Под знаком интеграла переходим к новой переменной. 4) Находим табличный интеграл. 5) Возвращаемся к старой переменной.
Интегральная сумма определенный интеграл, его геометрический смысл Пусть на отрезке
Обозначим через Определение. Определенным интегралом от функции
Замечание 1. Переменную под знаком интеграла можно обозначать любой буквой: Замечание 2. В отличие от неопределенного интеграла Геометрический смысл определенного интеграла.
Экономический смысл определенного интеграла. Пусть функция Теорема (достаточное условие существования определенного интеграла). Если функция Теорема о среднем. Если функция Т.о. теорема о среднем утверждает, что найдется такая точка Формула ньютона-лейбница Определенный интеграл с переменным верхним пределом Пусть
где
Определение. Функция Теорема 1. Если функция Теорема 2 (о производной интеграла по верхнему пределу). Пусть функция
Формула Ньютона-Лейбница. Теорема. Пусть функция
Значение определённого интеграла равно разности значений любой первообразной от подынтегральной функции, взятых при верхнем и нижнем пределах интеграла. Другими словами, Значение определённого интеграла равно приращению любой первообразной от подынтегральной функции на интервале интегрирования. Формула Ньютона-Лейбница позволяет находить определённый интеграл, обходя суммирование, при помощи первообразных функций.
|
||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 322; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.01 с.) |

 (1)
(1) не может быть непосредственно преобразован к табличному интегралу. Введем новую переменную
не может быть непосредственно преобразован к табличному интегралу. Введем новую переменную  :
:  . Тогда
. Тогда  ,
,  , т.е.
, т.е.  ,
,  . Т.к.
. Т.к.  , то эти производные равны, поэтому по следствию Лагранжа левая и правая части (1) отличаются на некоторую постоянную. Поскольку сами неопределенные интегралы определены с точностью до неопределенного постоянного слагаемого, то указанную постоянную в окончательной записи можно опустить.■
, то эти производные равны, поэтому по следствию Лагранжа левая и правая части (1) отличаются на некоторую постоянную. Поскольку сами неопределенные интегралы определены с точностью до неопределенного постоянного слагаемого, то указанную постоянную в окончательной записи можно опустить.■ некоторая первообразная для функции
некоторая первообразная для функции  . Тогда если вместо аргумента
. Тогда если вместо аргумента  подынтегральной функции
подынтегральной функции  и первообразной
и первообразной  подставить выражение
подставить выражение  , то это приведет к появлению дополнительного множителя
, то это приведет к появлению дополнительного множителя  перед первообразной:
перед первообразной:  , где
, где  и
и  - некоторые числа,
- некоторые числа,  .
. в виде:
в виде:  . Но
. Но  . Вынося постоянный множитель
. Вынося постоянный множитель  за знак интеграла и деля левую и правую части равенства на
за знак интеграла и деля левую и правую части равенства на  , приходим к
, приходим к  .
. задана функция
задана функция  (рис. 10.1).
(рис. 10.1).
 на
на 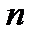 элементарных отрезков точками
элементарных отрезков точками  , где
, где  . На каждом отрезке разбиения выберем некоторую точку
. На каждом отрезке разбиения выберем некоторую точку  и положим
и положим  , где
, где  .
Сумму вида
.
Сумму вида  будем называть интегральной суммой для функции
будем называть интегральной суммой для функции  на отрезке
на отрезке  .
.
 максимальную из длин отрезков
максимальную из длин отрезков  , т.е.
, т.е.  .
. на отрезке
на отрезке  называется предел интегральной суммы при
называется предел интегральной суммы при  , т.е.
, т.е. . (10.1)
. (10.1) - нижний предел,
- нижний предел,  - верхний предел,
- верхний предел,  - подынтегральная функция,
- подынтегральная функция,  - подынтегральное выражение.
- подынтегральное выражение. и т. д.
и т. д. , который представляет семейство функций (первообразных), определенный интеграл
, который представляет семейство функций (первообразных), определенный интеграл  есть определенное число.
есть определенное число. Пусть на отрезке
Пусть на отрезке  криволинейной трапеции, ограниченной кривой
криволинейной трапеции, ограниченной кривой  , прямыми
, прямыми  ,
,  и осью абсцисс
и осью абсцисс  (рис.10.2) численно равна определенному интегралу от функции
(рис.10.2) численно равна определенному интегралу от функции 
 описывает изменение производительности некоторого производства с течением времени. Тогда объем продукции
описывает изменение производительности некоторого производства с течением времени. Тогда объем продукции  , произведенной за промежуток времени
, произведенной за промежуток времени  , равен
, равен  .
. непрерывна на отрезке
непрерывна на отрезке  , то она интегрируема на этом отрезке.
, то она интегрируема на этом отрезке. непрерывна на отрезке
непрерывна на отрезке  , то найдется такое значение
, то найдется такое значение  , что
, что  .
. из отрезка
из отрезка  , что площадь под кривой
, что площадь под кривой  равна площади прямоугольника со сторонами
равна площади прямоугольника со сторонами  и
и  .
. - непрерывная на отрезке
- непрерывная на отрезке  - ее первообразная. Рассмотрим определенный интеграл
- ее первообразная. Рассмотрим определенный интеграл , (10.2)
, (10.2) . При изменении
. При изменении  меняется и определенный интеграл (10.2), т.е. он является функцией верхнего предела интегрирования
меняется и определенный интеграл (10.2), т.е. он является функцией верхнего предела интегрирования  :
: , (10.3)
, (10.3) непрерывна на отрезке
непрерывна на отрезке  то функция
то функция  так же непрерывна на
так же непрерывна на  .
. непрерывна на отрезке
непрерывна на отрезке  .
. .
.


