Метод численного интегрирования методом трапеций

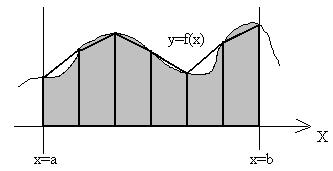
Рис. 16.13. - Интерпретация определенного интеграла.

Геометрической интерпретацией определенного интеграла является площадь криволинейной трапеции, ограниченной заданной подынтегральной функцией f(x), осью абсцисс и прямыми, представляющими собой вертикальные линии, которые проходят через точки, соответствующие пределам интегрирования (рис. 16.13).

Метод решения заключается в вычислении этой площади. Так как не существует простых математических формул для вычисления площади криволинейной фигуры, то эту криволинейную фигуру заменяют набором элементарных фигур – прямоугольников или прямоугольных трапеций. Естественно, что в методе трапеций – прямоугольными трапециями. Для этого разобьем участок интегрирования (ось Х в пределах от a до b) на n одинаковых отрезков и на каждом отрезке построим прямоугольные трапеции с основаниями равными значениям подынтегральной функции на краях отрезка и высотой равной длине отрезка на участке интегрирования (b-a)/n. Вид i-го отрезка интегрирования приведен на рис. 16.14.

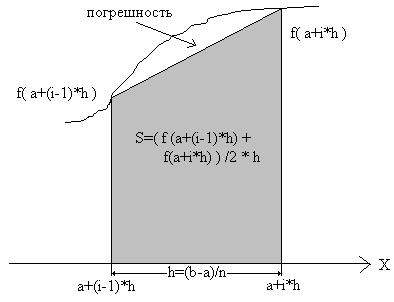
Рис. 16.14. – Прямоугольная трапеция

Площадь прямоугольной трапеции вычисляется по известной формуле S=(L_осн1+L_осн2)/2 * h. Для трапеции, построенной на i-ом отрезе,

L_осн1=f(a+(i-1)*h);

L_осн2=f(a+i*h);

S=(f(a+(i-1)*h) + f(a+i*h))/2*h, где h=(b-a)/n

Таким образом, площадь под интегральной функцией заменяем суммой площадей n прямоугольных трапеций на этом же участке интегрирования. Естественно, такая замена приводит к некоторой ошибке, которую называют точностью интегрирования. Чем больше величина n, тем меньше ошибка, т.е. выше точность интегрирования.

Предложенный метод интегрирования запишем следующим образом:

1) h:=(b-a)/n

2) S:=0

3) "i:=1..n: S:=S+ f(a+(i-1)*h) + f(a+i*h)

4) S:=S/2*h

Так как в третьем действии дважды вычисляются одинаковые значения функции f (кроме f(a) b f(b)), то метод решения можно упростить (что делать при высокой скорости вычислений необязательно):

1) h:=(b-a)/n

2) S:=f(a)+f(b)

3) "i:=1..n-1: S:=S+ 2 * f(a+i*h)

4) S:=S/2*h

 

Спецификация на разрабатываемую подпрограмму

1. Назначение: вычисление определенного интеграла методом трапеций.

2. Имя: integral.

3. Вид: функция.

4. Перечень входных и выходных данных:

Таблица 16.7. Перечень параметров

Статус	Назначения	Имя	Тип	Вид
Вход	подынтегральная математическая функция	f	Подпрограммный тип tf	параметр-подпрограмма
Вход	начало участка интегрирования	a	Real	параметр-значение
Вход	конец участка интегрирования	b	Real	параметр-значение
Вход	количество разбиений	n	Integer	параметр-значение
Возвра-щаемое значение	определенный интеграл	integral	Real	-

Математическая подынтегральная функция в общем виде всегда имеет один аргумент вещественного типа, и результат вычисления при заданном аргументе представляет собой вещественное число. Поэтому подпрограммный тип tf должен быть определен следующим образом:

type tf=function(x:real):real;

5. Заголовок подпрограммы:

function integral (f:tf; a,b:real; n:integer): real;

Информационная модель

Таблица 16.8. Информационная модель

Назначение	Имя	Тип
Для накопления суммы	S	real
Высота трапеции (шаг интегрирования)	h	real
Номер трапеции (отрезка интегрирования)	i	integer

Текст подпрограммы

type tf=function(x:real):real;

 

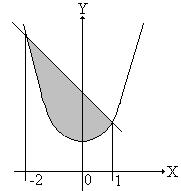
function integral(f:tf;a,b:real;n:integer):real;

var h,s:real;

i:integer;

begin

h:=(b-a)/n;

S:=f(a)+f(b);

for i:=1 to n-1 do

S:=S+ 2 * f(a+i*h);

S:=S/2*h;

integral:=S

end;

Пример использования функции integral

Постановка задачи

Решим следующую задачу: определить площадь S, ограниченную параболой y=x²+1 и прямой y=3-x. Для того, чтобы получить пределы интегрирования, аналитически определим точки пересечения этих линий. Совместное решение уравнений дает пределы интегрирования от -2 до 1.

Рис. 16.15 – Графическая модель задачи

Метод решения

Решение задачи с учетом существования функции integral сводится к вычислению

S=integral(F1,-2,1,10000)-integral(F2,-2,1,10000).

Здесь применяем 10000 разбиений участка интегрирования, помня, что, чем больше количество разбиений, тем точнее вычисления. Реализация такого метода решения тривиальна.

В методе решения F1 и F2 представляют собой подпрограммы, соответствующие подынтегральными функциям. Интерфейс этих функций соответствует типу tf.

Метод решения функции F1: F1=3-x.

Метод решения функции F2: F2= x²+1.

Попутно определим требования к подпрограммам, которые являются фактическими параметрами

1. Эти подпрограммы не могут быть стандартными;

2. Их имена не могут совпадать с именами стандартных подпрограмм;

3. Подпрограммы должны быть оттранслированы с параметром «дальний вызов», так как реализация языка Паскаль требует, чтобы фактический параметр-подпрограмма имел полный адрес (сегмент и смещение) Это достигается с помощью директивы «включить дальний вызов» {$F+}

Текст программы

 

program primer;

type tf=function(x:real):real;

 

function integral(f:tf;a,b:real;n:integer):real;

var h,s:real;

i:integer;

begin

h:=(b-a)/n;

S:=f(a)+f(b);

for i:=1 to n-1 do

S:=S+ 2 * f(a+i*h);

S:=S/2*h;

integral:=S

end;

 

{$f+} {включение дальнего вызова}

 

{реализация первой подынтегральной функции}

function F1(x:real):real;

begin

F1:=3-x

end;

 

{реализация второй подынтегральной функции}

function F2(x:real):real;

begin

F2:=sqr(x)+1

end;

 

{$f-} {отключение дальнего вызова}

 

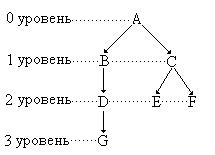
var s:real;{выходной параметр программы – площадь заштрихованной области}

begin

S:=integral(F1,-2,1,10000)-integral(F2,-2,1,10000);

writeln('Площадь=',S)

end.

16. 12. Блочная структура программ.
Области действия описаний

Как правило, процедуры и функции располагаются в разделах процедур и функций, то есть являются вложенными внутрь программ или других подпрограмм. При таком вложении описание подпрограммы есть составляющая блока, и сама подпрограмма включает в себя блок, то можно ввести понятия внешний и внутренний блок.

Внешний блок – это блок, в который вложена подпрограмма. Внутренний блок - сама подпрограмма. Все описания, расположенные во внешних для данной подпрограммы блоках, называются глобальными по отношению к блоку, который образует данная подпрограмма. Все описания, расположенные во внутреннем блоке называются локальными. Можно ввести понятие уровень вложенности. Если в разделе описания процедур и функций описаны две или более подпрограмм, то говорят, что эти подпрограммы одного уровня вложенности. По отношению к внешнему блоку они являются внутренними. По отношению между самими подпрограммами мы не можем использовать термины внешняя или внутренняя, так как они одного уровня вложенности. Если в разделе описания процедур и функций внешнего блока вложена подпрограмма, внутри которой в таком же разделе расположена другая подпрограмма, то мы говорим о разном уровне вложенности этих подпрограмм. Для третьего блока, представляющего собой самую внутреннюю подпрограмму, оба блока, в которые она вложена, будут внешними. Уровень вложенности этой подпрограммы 2. Для второго блока третий блок будет внутренним, а первый - внешним. Уровень вложенности второго блока 1. Для первого блока (самого внешнего) второй и третий блоки будут внутренними. Уровень вложенности первого блока 0, т.е. этот блок является основной программой.

Для примера рассмотрим структуру блоков, предложенную автором языка (рис.16.16). Здесь в седьмой раздел программы A вложены две подпрограммы B и C. В подпрограмму В вложена подпрограмма D. В свою очередь в подпрограмму D вложена подпрограмма G. В подпрограмму С вложены две подпрограммы E и F.

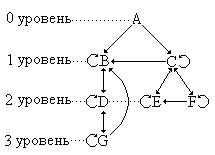
Рис. 16.16. - Пример блочной структуры

Разберемся со сферой действия описаний. Описания меток действуют только внутри раздела операторов блока, в котором они описаны. Все остальные описания действуют не только внутри блока, в котором они описаны, но и во всех внутренних блоках, вложенных в данный блок (вне зависимости от глубины вложенности). При этом казалось, что могут возникнуть конфликты между глобальными и локальными описаниями, так как в разных блоках одинаковыми именами могут быть поименованы разные понятия. Для того чтобы таких конфликтов не возникало, принято следующее правило - все имена, определяемые в локальных описаниях, отменяют действия совпадающих имен, описанных в глобальных описаниях. На рис. 16.17 показано расположение блоков из примера по уровням. Здесь линиями со стрелками показано действие глобальных описаний. Так в блоке G действуют описания внешних блоков D, B, A.

Рис. 16.17. - Расположение блоков по уровням и действие глобальных описаний

Особо рассмотрим доступ к подпрограммам. Любая подпрограмма может быть вызвана:

a) из раздела операторов блока, в котором она описана;

b) из раздела операторов самой себя (прямая рекурсия);

c) из раздела операторов любой внутренней подпрограммы по отношению к данной (косвенная рекурсия);

d) из раздела операторов любой подпрограммы, описанной ранее в том же блоке, где и данная подпрограмма.

Эти правила можем переформулировать следующим образом – любая подпрограмма может вызывать на исполнение:

a) любую подпрограмму, описанную в разделе подпрограмм данной;

a) саму себя (прямая рекурсия);

b) все внешние подпрограммы по отношению к данной (косвенная рекурсия);

c) подпрограммы, описанные ранее на том же уровне вложенности.

Взаимодействие блоков (подпрограмм) из примера показано на рис. 16.18.

Рис. 16.18 - Пример взаимодействия между блоками

Здесь линиями со стрелками показаны возможности вызова подпрограмм на выполнение (стрелки указывают направление вызова). Так, например, из программы А могут быть вызваны только подпрограммы В и С, которые вложены в седьмой раздел. Из подпрограммы F могут быть вызваны сама подпрограмма F (прямая рекурсия), подпрограмма С, в которую она вложена (косвенная рекурсия), и подпрограмма Е (находится на одном уровне и описана ранее). з программы А могут быть вызваны подпрограммы B и С. В таблице 16.9 для перечислены все возможные взаимодействия между блоками. Здесь основной алгоритм – блок, из которого производится вызов подпрограммы, вспомогательный алгоритм – вызываемая подпрограмма.

Таблица 16.9. Пример взаимодействия между блоками