
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
I. Постановка задачи и выбор математической моделиСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Постановку задачи можем записать как функционал F(k)=k!, определяющийся следующим образом F(0) = 1, F(k) = 1*2*3*...*k, при II. Спецификация 1) Назначение: вычисление факториала натурального числа 2) Имя: F 3) Вид: функция, т.к. результат - одно натуральное число, являющееся факториалом входного параметра. 4) Перечень параметров: Таблица 16.1. Перечень параметров
Типом результата функции выбран тип longint, так как факториал быстро растущая функция – 0!=1; 1!=1; 2!=2; 3!=6; 4!=24; 5!=120; 6!=720; 7!=5040; 8!=40320; 9!=362880 и т.д. Исходя из этого, аргумент не должен превышать значения 12. 5) Заголовок подпрограммы: FUNCTION F(k:BYTE):LONGINT; III. Метод решения Определенная математическая модель F(0) = 1, F(k) = 1*2*3*...*k, при k, принадлежащем множеству натуральных чисел может быть реализована в виде циклического алгоритма накопления произведения. Существует общий алгоритм накопления произведения заданного числа последовательных значений. Вначале переменной, в которой должен быть накоплен результат, присваивается единица (F:=1). Затем значение этой переменной последовательно домножается на каждый сомножитель (для всех i от 1 до k выполняется действие F:=F*i). В этом алгоритме новое значение F формируется через предыдущее, т.е. F находится в левой и правой частях оператора присваивания, являясь в правой части составной частью выражения. Из-за этого возникает неоднозначная трактовка - F переменная или обращение к функции? Для устранения этой неоднозначности было в Паскале принято следующее правило: если имя функции появляется в выражении, то это вызов функции, если в левой части оператора присваивания, то это переменная, в которой формируется результат функции (переменная-результат). Естественно, вызов подпрограммы может использоваться при выполнении этой же подпрограммы. Такая ситуация называется рекурсивным обращением к подпрограмме, которое рассмотрим позднее. Таким образом, метод решения можно сформулировать так 1) y:=1 2) "i:=1..k: y:=y*i 3) F:=y Последнее действие связано с тем, что результат функции обязательно должен находиться в переменной, совпадающей по имени с именем функции.
IV. Информационная модель Необходимо помнить, что информационная модель подпрограммы (табл. 16.2) включает в себя только промежуточные переменные, так как входные и выходные переменные определены в перечне параметров подпрограммы. Таблица 16.2. Информационная модель
V. Текст подпрограммы
{Функция F вычисляет факториал заданного целого положительного числа. Имя функции: F. Входной параметр: параметр-значение типа byte (целое положительное число). Параметр-результат: целое число типа longint. } function F(k:word):longint; var y:longint;{для накопления произведения} i:byte;{текущий сомножитель} begin y:=1; for i:=1 to k do y:=y*i; F:=y end;{function F}
Метод решения задачи с учетом разработанных подпрограмм
Метод решения состоит из одного действия: При этом необходимо проверять правильность исходных данных – n и m должны Информационная модель задачи Информационная модель задачи приведена в табл. 16.3.
Таблица 16.3. Информационная модель
Текст программы В тексте программы по правилам структурного программирования раздел текстов подпрограмм располагается ранее раздела переменных, чтобы сделать эти переменные недоступными для использования в действиях подпрограмм. program sochet; {Программа служит для вычисления числа сочетаний C из n по m}
label inp;{используется при повторе ввода из за ошибки ввода}
{Функция F вычисляет факториал заданного целого положительного числа. Входной параметр: параметр-значение типа byte (целое положительное число). Параметр-результат: целое число типа longint. } function F(k:word):longint; var y:longint;{для накопления произведения} i:byte;{текущий сомножитель} begin y:=1; for i:=1 to k do y:=y*i; F:=y end;{function F}
var n,m:word;{исходные данные} C:word;{результат - число сочетаний}
begin
{ ввод исходных данных }
inp: writeln('Для задачи вычисления числа сочетаний из n по m'); writeln('введите значения n и m в пределах от 1 до 12, n>=m.');
{ отключение системы прерываний на ошибки ввода-вывода и выхода из диапазона значений } {$I-} {$R-} readln(n,m); { включение системы прерываний на ошибки ввода-вывода и выхода из диапазона значений } {$I+} {$R+} { проверка правильности ввода. При ошибке - повторение ввода } if (IOResult<>0)or(n<m)or(n>12)or(m>12)or(n<1)or(m<1) then begin writeln('ОШИБКА ВВОДА'); goto inp end;
{ вычисление числа сочетаний } C:=F(n) div (F(m)*F(n-m));
{ вывод результата } writeln('Число сочетаний из ',n,' по ',m,' = ',C)
end. Обратите внимание, что контроль за правильностью ввода исходных данных возложен на программу. Отключение и включение этой системы производится с помощью директив транслятору, приведенных в программе. Помните, что при отключенной системе прерываний при выполнении операций ввода-вывода формируется значение системной переменной (результат выполнения операции ввода-вывода), значение которой может быть получено с помощью системной функции IOResult. Ненулевое значение этой функции - сигнал об ошибке при выполнении последней операции ввода-вывода. Исполнение программы sochet 0. Распределение оперативной памяти показано на рис. 16.4.
Рис. 16.4. – Распределение ОП 1. В результате выполнения оператора обращения к процедуре вывода на экране появляется текст: Для задачи вычисления числа сочетаний из n по m 2. В результате выполнения оператора обращения к процедуре вывода на экране появляется текст: введите значения n и m в пределах от 1 до 16, n>=m. 3. При выполнении оператора обращения к процедуре ввода ЭВМ ожидает от человека два значения типа byte. Пусть человек нажимает клавиши: 3 пробел 2 Enter
4. Вычисляется условие наличия ошибки ввода исходных данных, получается результат FALSE 5. Выполняется оператор присваивания C:=F(n) div (F(m)*F(n-m)) 6. Создается стек выражения, в который переносятся значения, знаки операций и круглые скобки, изменяющие порядок выполнения действий (рис. 16.5)
Рис. 16.5. – Стек вычисления выражения При заполнении стека трижды встречаются вызовы функции F. В соответствии с правилами вычисления выражения из этих трех обращений первым обрабатывается вызов F(m). Рассмотрим выполнение этого вызова: 6.1. Создается динамический экземпляр данных подпрограммы (рис. 16.6), в который входят - переменная, совпадающая по имени с именем функции F. Тип этой переменной определяется типом результата функции longint; - переменная k, соответствующая одноименному формальному параметру-значению типа byte; - две локальных переменных y типа longint и i типа byte;
Рис. 16.6. – Динамический экземпляр данных функции F 6.2. Осуществляется передача фактических параметров в подпрограмму. В нашем случае имеется один фактический параметр m. Он подставляется на место формального параметра-значения k. Поэтому фактический параметр вначале вычисляется. Полученное значение 2 заносится в динамический экземпляр данных в переменную k; 6.3. Выполняются действия подпрограммы. Подробно рассматривать эти действия не будем. В результате сформируется содержимое динамического экземпляра данных подпрограммы, приведенное на рисунке. 6.4. По завершению подпрограммы значение автоматической переменной F равное 2 передается в стек, из которого вызывалась функция. Динамический экземпляр данных подпрограммы уничтожается и продолжает вычисляться вышеуказанный стек.
Аналогично обрабатываются вызовы F(n-m) и F(n). После заполнения содержимое стека выглядит следующим образом:
Рис. 16.7. – Содержимое стека В результате выполнения оператора переменной С будет присвоено значение 3; 7. В результате выполнения оператора обращения к процедуре вывода на экране появляется сообщение: Число сочетаний из 3 по 2 = 3 Пример использования процедур Для того, чтобы сформулировать различия между процедурами и функциями решим поставленную задачу с использованием процедуры. Разработка подпрограммы
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 482; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.89.181 (0.012 с.) |


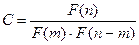
 n
n
 m
m
 C
C

 ЭВМ размещает значения в ОП: 3 n 2 m
ЭВМ размещает значения в ОП: 3 n 2 m F
F
 k
k


 y
y





