
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формальное исполнение вызова рекурсивной функцииСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Рассмотрим вычисление y=3! с использованием рекурсивной функции F. Необходимо выполнить оператор y:=F(3). При выполнении этого оператора в оперативной памяти существует участок для хранения значения y.
По правилам выполнения оператора присваивания, вначале вычисляется выражение F(3), стоящее справа от знака присваивания. Затем полученное значение заносится в участок памяти у.
Так как выражение состоит из вызова функции, то при его вычислении работает механизм обработки вызова подпрограммы: 1) Создается динамический экземпляр данных, который существует до окончания выполнения этой подпрограммы. Этот динамический экземпляр данных включает в себя участки памяти, отведенные под параметры-значения и локальные переменные подпрограммы, а также под переменную-результат для функции. При вычислении выражения F(3) порождается динамический экземпляр данных функции F:
2) Осуществляется передача фактических параметров. В поле параметра-значения передается значение выражения, подставленное на место формального параметра при обращении к функции, т.е. 3;
3)Затем выполняются действия вызванной подпрограммы. В функции F выполняется условный оператор. Вычисляется условие 3=0 (ложь); 4) Так как результат "ложь", то выполняется оператор присваивания F:=F(k-1)*k
5) При заполнении стека вызывается функция F(k-1). Возникает новый динамический данных функции F:
6) В этот экземпляр передается число 2, как значение параметра-значения; 7) Начинает выполняться функция F. (Заметьте, что вычисление выражения F(2)*3 не закончено). Условие 2=0 имеет значение "ложь"; 8) Поэтому, выполняя оператор F:=F(k-1)*k, вычисляется выражение F(1)*2. Появляется новый динамический данных функции F:
9) Начинают выполняться действия функции F. Условие 1=0 имеет значение "ложь". При выполнении оператора F:=F(k-1)*k, вычисляется выражение F(0)*1. Порождается новый динамический данных функции F:
10) Перед выполнением функции F(0) напомним о цепочке выражений, которая возникла при вычислении F (рис. 16.10).
Рис. 16.10 – Динамические экземпляры данных при рекурсии а) Продолжаем выполнение функции F(0). Условие 0=0 имеет значение "истина", поэтому переменной-результату функции присваивается значение 1. Функция F(0) выполнилась;
б) значение 1 поступило для вычисления выражения 1*F(0). Динамический экземпляр данных для функции F(0) удалился из памяти; в) вычисляется выражение 1*1, получается 1.Функция F(1) выполнилась; г) значение 1 поступило для вычисления выражения 2*F(1). Динамический экземпляр данных для функции F(1) удалился из памяти; д) вычисляется выражение 2*1, получается 2. Функция F(2) выполнилась; е) значение 2 поступило для вычисления выражения 3*F(2), динамический экземпляр данных для функции F(2) удалился из памяти; ж) вычисляется выражение 2*3, получается 6. Функция F(3) выполнилась; з) значение 6 поступило для вычисления выражения F(3), динамический экземпляр данных для функции F(3) удалился из памяти; з) значение 6 является результатом вычисления выражения F(3); и) значение 6 записывается в память под именем y.
Процесс обратных изменений (свертка) при вычислении y=3! приведен на рис. 16.11.
Рис. 16.11. -Процесс свертки при вычислении y=3! Из приведенного примера становится ясным, что рекурсия свойственна циклическим итерационным алгоритмам. При выполнении рекурсивных подпрограмм возникает большое количество динамических экземпляров данных, что может привести к переполнению памяти, выделенной под эти данные операционной средой. Подпрограммные типы Если в качестве входного параметра в подпрограмму передается другая подпрограмма, то заголовок этой второй подпрограммы должен соответствовать подпрограммному типу, имя которого указано в заголовке первой подпрограммы для формального параметра-подпрограммы. Подпрограммный тип определяется в разделе описания нестандартных типов внешнего блока, из которого вызывается первая подпрограмма. Подпрограммный тип определяет интерфейс, которому должна соответствовать фактическая подпрограмма, которая является фактическим входным параметром. Подпрограммный тип определяет вид подпрограммы (процедура или функция), количество, порядок следования, типы и виды параметров. Синтаксические диаграммы определения подпрограммных типов приведены на рис. 16.12. Имена формальных параметров при определении подпрограммного типа никакой информации в себе не несут и все равно какими они заданы, главное - что с их помощью определяется количество параметров, их вид и порядок следования
Пример использования подпрограммного типа Подпрограммы в качестве параметров используются в задачах, в которых один и тот же математический метод решения может применяться для обработки данных вычисляющихся с помощью разных действий. В свою очередь эти разные действия оформляются в виде разных вспомогательных алгоритмов, имеющих одинаковый интерфейс. Очень часто такие задачи решаются в области численных экономико-математических методах. Одним из примеров является задача численного интегрирования. Можно выбрать один любой метод численного интегрирования и применять его для любых непрерывных математических функций.
|
|||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 420; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.242.223 (0.007 с.) |








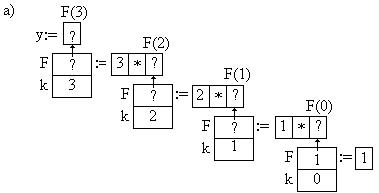

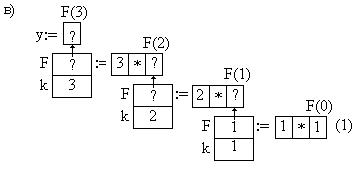





 Рис. 16.12. - Синтаксические диаграммы определения подпрограммных типов
Рис. 16.12. - Синтаксические диаграммы определения подпрограммных типов


