
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уточнение корней методом половинного деленияСодержание книги
Поиск на нашем сайте
Численные методы (Методические указания и задания)
Составители С.И. Смуров В.А. Таланова С.П. Бобков
Иваново 2003 В методических указаниях рассматриваются методы приближенного вычисления определенного интеграла, численного решения алгебраических и трансцендентных уравнений, вопросы математической обработки экспериментальных данных. Даны примеры решения задач и задания для самостоятельной работы.
Указания составлены в соответствии с программой и одобрены решением цикловой методической комиссией по физико-математическим дисциплинам.
1. ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ
Вычислить определенный интеграл
где Однако во многих случаях не удается найти никакой аналитической формулы в виду невозможности определения В таких случаях приходится применять методы численного интегрирования. Основной принцип построения всех приближенных формул численного интегрирования состоит в том, что интервал интегрирования разбивается на множество меньших отрезков, внутри которых подынтегральная кривая
Метод прямоугольников
Вычисление интеграла
Рис. 1. 1. Разобьем интервал интегрирования на n равных частей, каждая длиной h=(b-a)/n. Приближенное значение интеграла получается в виде сумм площадей n прямоугольников, высота которых равна значению f(x) на левом краю каждого подинтервала, т.е. формула численного интегрирования имеет вид (I. 2.):
и называется формулой «левых» прямоугольников. Если в качестве приближенного значения площади для каждого подинтервала принять площадь прямоугольника, высота которого равна значению f(x) на правом краю подинтервала, то формула численного интегрирования будет иметь вид (I. 3.):
и называется формулой «правых» прямоугольников.
Метод трапеций
В соответствии с полученными ранее формулами «левых» и «правых» прямоугольников истинное значение интеграла лежит между приближенными значениями, определяемыми по этим формулам (рис. I. 2), т.е. лучшую формулу численного интегрирования можно получить, взяв среднее арифметическое этих значений:
Рис. 1. 2
Эта формула (I. 4) описывает метод трапеций для численного интегрирования, т.е. приближенное значение интеграла
1. 3. Метод парабол (метод Симпсона)
Это наиболее широко известный и применяемый метод численного интегрирования. Метод аналогичен рассмотренным ранее методам прямоугольников и трапеций: интервал интегрирования разбивается на множество более мелких отрезков; однако для вычисления площади под каждым из отрезков через три последовательных ординаты разбиения проводится квадратичная парабола (рис. 1. 3).
Рис. 1. 3
Действительно, определяя y0, y1, y2:
имеем т.е. окончательно или
Последняя формула (I.6) называется формулой Симпсона. Поскольку в методе Симпсона парабола проводится через три ординаты на концах двух соседних интервалов, то при реализации этого метода необходимо требовать, чтобы «n» было четным числом.
Задания. Вычислить определенный интеграл
2. ПРИБЛИЖЕННОЕ РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ И ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ
Если алгебраическое или трансцендентное уравнение достаточно сложно, то довольно редко удается точно найти его корни. Кроме того, в некоторых случаях уравнение может содержать коэффициенты, известные лишь приблизительно, поэтому сама задача о точном нахождении корней теряет смысл. Уравнение с одним неизвестным в общем виде можно записать так:
где f(x) – определена и непрерывна в некотором интервале [a, b]. Всякое значение X*, обращающее функцию f(x) в нуль (f(X*)=0), называется корнем уравнения (2.1). Будем предполагать, что уравнение имеет лишь изолированные корни, т.е. для каждого корня существует окрестность, не содержащая других корней этого уравнения. Приближенное нахождение корней уравнения складывается из двух этапов. 1) Отделение корней. Отделить корни – это значит разбить всю область на отрезки, в каждом из которых содержится только один корень. Отделение корней можно произвести аналитически или графически.
В зависимости от того, какие функции входят в уравнение, разделяют их на два класса: алгебраические и трансцендентные. Функция называется алгебраической, если для получения ее значения нужно выполнить арифметические операции и возведение в степень с рациональным показателем. Трансцендентные функции – показательная, логарифмическая, тригонометрическая, обратная тригонометрическая. 2) Уточнение корней до заданной точности. Сформируем теоремы, которые необходимы для отделения коней. Теорема 1. Если непрерывна функция y=f(x) принимает на концах отрезка [a, b] значение разных знаков, т.е. f(a)f(b)<0, то на этом отрезке содержится по меньшей мере один корень уравнения (2.1) (рис. 2.1)
Рис. 2.1 Теорема 2. Если функция y=f(x) непрерывна на отрезке [a, b], принимает на концах отрезка значения разных знаков, а производная f ’ (x) сохраняет знак внутри отрезка [a, b], то внутри отрезка существует единственный корень уравнения f(x)=0 (рис. 2.2)
 
  
Рис. 2.2 Для того, чтобы графически отделить корни уравнения f(x)=0 строят график функции y=f(x). Действительные корни уравнения можно определить как абсциссы точек пересечения кривой с осью (рис. 2.3)
Рис. 2.3
Практически бывает более выгодным заменить уравнение (2.1) равносильным ему уравнением
   Искомые корни получим как абсциссы точек пересечения этих графиков (рис. 2.4) Искомые корни получим как абсциссы точек пересечения этих графиков (рис. 2.4)
Рис. 2.4 Пример. Отделить графически корень уравнения
Решение. Запишем уравнение в виде
 Построим график (рис. 2.5) функций Построим график (рис. 2.5) функций 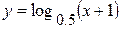 и и  . .
Рис. 2.5 Из графика следует, что корень уравнения находится на отрезке Графический метод дает возможность грубо определить интервалы изоляции корня. Далее корень уточняется одним из способов описанных ниже.
Метод итераций
Решение уравнения вида x1=f(x0); x2=f(x1) и т.д. Если производная f ’ (x) удовлетворяет условию При реализации метода итераций на ЦВМ, исходя из предположения, что метод может не сойтись, необходимо предусмотреть в программе следующие условия окончания работы: 1. Останов, как только 2. Останов, как только число итераций достигнет N. Величины
Метод хорд
Пусть на отрезке [a, b] функция f(x) непрерывна, принимает на концах отрезка значение разных знаков, а производная f ’(x) сохраняет знак. В зависимости от знака второй производной возможны следующие случаи расположения кривых (рис. 2.7., 2.8): 1. f(a)<0, f(b)>0, f ‘(x)>0 – функция возрастает а) f ’’(x)>0 (кривая вогнута вниз) б) f ’’(x)<0 (кривая вогнута вверх)
Рис. 2.7
2. f(a)>0, f(b)<0, f ‘(x)<0 – функция убывает а) f ’’(x)>0 б) f ’’(x)<0
Рис. 2.8
Рассмотрим случай, когда f ’(x) и f ’’(x) имеют одинаковые знаки. (рис. 2.9.)
3. f(a)<0, f(b)>0, f ‘(x)>0 – функция возрастает а) f ’’(x)>0 (кривая вогнута вниз) б) f ’’(x)<0 (кривая вогнута вверх)
f ‘(x)>0, f ’’(x)>0
Рис. 2.9
График функции проходит через точки A0(a, f(a)) и B(b, f(b)). Искомый корень уравнения (точка ξ) нам известен, вместо него возьмем точку x1 пересечения хорды A0B с осью абсцисс это и будет приближенное значение корня. Уравнение хорды A0B: Найдем значение x=x1, для которого y=0
Теперь корень находится на отрезке [x1, b]. Применим метод хорд к этому отрезку. Проведем хорду, соединяющую точки A1(x1, f(x1)) и B и найдем точку x2 – точку пересечения хорды A1B с осью ox
Продолжая этот процесс, находим:
В этом случае конец b отрезка [a, b] остается неподвижным, а конец a перемещается. Формула (2.2) носит название формулы метода хорд. Вычисление по формуле (2.2) продолжаем до тех пор, пока не достигнем заданной точности, т.е. должно выполняться условие:
Теперь рассмотрим случай, когда первая и вторая производные имеют разные знаки, т.е. f ‘(x) f ’’(x)<0 (рис. 2.10).
  
Рис. 2.10
Соединим точки A(a, f(a)) и B0(b, f(b)) хордой AB0. Точку пересечения хорды AB0 с осью ox будем считать первым приближением корня. В этом случае, очевидно, неподвижным концом отрезка будет являться конец a. Запишем уравнение хорды AB0:
Отсюда найдем x1, полагая y=0: Теперь корень
Условие окончания вычислений: Итак, если f ‘(x) f ’’(x)>0 приближенное значение корня находят по формуле (2.2), если f ‘(x) f ’’(x)<0, то по формуле (2.3). Практически выбор той или иной формулы осуществляют, пользуясь следующим правилом: неподвижным концом отрезка является тот, для которого знак функции совпадает со знаком второй производной.
2. 4. Метод касательных (Метод Ньютона)
Пусть корень уравнения f(x)=0 отделен на отрезке [a, b]. Причем производные f ‘(x) и f ’’(x) непрерывны и сохраняют постоянные знаки. Геометрический смысл метода касательных состоит в том, что дуга кривой y=f(x) заменяется касательной к этой кривой. Рассмотрим случай, когда f ‘(x) f ’’(x)>0, т.е. f ‘(x) и f ’’(x) имеют одинаковые знаки (рис. 2.11)
Рис. 2.11
Проведем касательную к кривой y=f(x) в точке B0(b, f(b)). Уравнение касательной в точке B0: y-f(b)=f ’(b)(x-b). Полагая y=0, найдем Теперь Применяя метод еще раз для отрезка
Пусть теперь f ‘(x) f ’’(x)<0 (рис. 2.12)
Рис. 2.12
Если снова провести касательную к кривой в точке B, то она пересечет ось ox в точке не принадлежащей отрезку [a, b]. Поэтому проведем касательную в точке A0(a, f(a)). Ее уравнение y-f(a)=f ‘(a)(x-a). Находим x1, полагая y=0
Корень
Сравнивая формулы (2.4) и (2.5) между собою, замечаем, что они отличаются друг от друга только выбором начального приближения: в первом случае за x0 принимают конец b отрезка, во втором – конец a. При выборе начального приближения корня необходимо руководствоваться правилом: за начальную точку следует выбрать тот конец отрезка [a, b], в котором знак функции совпадает со знаком производной. Условие окончания вычислительного процесса:
Линейная интерполяция
В тех случаях, когда нет необходимости в отыскании приближенного выражения функции y=f(x), заданной таблично, можно использовать линейную интерполяцию, которая состоит в следующем. Отыскивается интервал [xi+1, xi], в который попадает значение На отрезке [xi-1, xi] заменим дугу кривой y=f(x) стягивающей ее хордой MN (рис. 2.3).

Рис. 3.2 Уравнение прямой, проходящей через точки В качестве приближенного значения функции
Метод наименьших квадратов
При интерполировании основным условием является совпадение значений функции и значений интерполяционного многочлена в узлах интерполяции. Однако при большом количестве узлов интерполяции получается высокая степень многочлена, что затрудняет вычисление. Кроме того, экспериментальные данные, полученные в результате измерений или наблюдений, могут содержать ошибки, которые вызваны несовершенством измерительных приборов, различными случайными факторами. Построение аппроксимирующего многочлена с условием обязательного прохождения его графика через эти экспериментальные точки будет означать повторение ошибок. Поэтому иногда целесообразней строить многочлен, график которого проходит «близко» от заданных точек. Итак, пусть при изучении неизвестной функциональной зависимости y от x получена таблица значений:
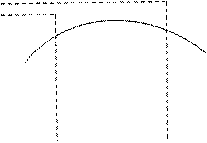
Нужно найти эмпирическую зависимость y=f(x), значение которых при x=xi мало отличались бы от опытных данных yi. График функции y=f(x), вообще говоря, не проходит через точки (xi, yi), как в случае интерполяции, что приводит к сглаживанию экспериментальных данных (рис. 3.3)

Рис. 3.3 Построение эмпирической формы состоит из двух этапов: 1) выбор общего вида зависимости; 2) выбор наилучших значений параметров, входящих в формулу. Метод наименьших квадратов не дает возможности выбрать вид зависимости, он позволяет лишь оптимально подобрать параметры приближающей функции. Вид зависимости выбирается из каких-либо дополнительных соображений: физических, геометрических т.д. Будем считать, что тип эмпирической зависимости выбран, и ее можно записать в виде: В каждой точке xi вычислим разность между табличным значением функции yi и вычисленным значением
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |

 , где
, где  – непрерывная функция x в интервале
– непрерывная функция x в интервале 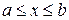 , можно с помощью аналитической формулы, если использовать прием формального интегрирования по формуле Ньютона-Лейбница (I. I.)
, можно с помощью аналитической формулы, если использовать прием формального интегрирования по формуле Ньютона-Лейбница (I. I.)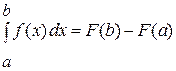 , (I. I.)
, (I. I.)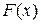 – первообразная функция для заданной функции
– первообразная функция для заданной функции  заменяется с некоторой степенью точности более простыми функциями, интегралы от которых можно вычислить, используя ординаты на концах отрезков.
заменяется с некоторой степенью точности более простыми функциями, интегралы от которых можно вычислить, используя ординаты на концах отрезков.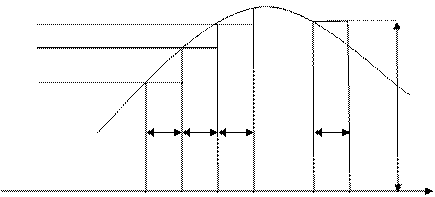
 или
или 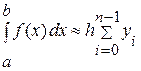 (I. 2.)
(I. 2.)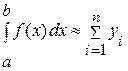 (I. 3.)
(I. 3.)

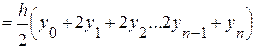
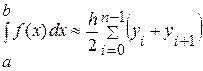 . (I. 4)
. (I. 4) получается в виде суммы площадей «n» трапеций.
получается в виде суммы площадей «n» трапеций.

 Формулу Симпсона выведем проводя параболу через три ординаты на концах двух соседних интервалов и складывая получившиеся при этом площади.
Формулу Симпсона выведем проводя параболу через три ординаты на концах двух соседних интервалов и складывая получившиеся при этом площади.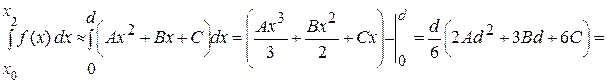
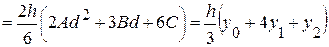
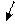 .
.


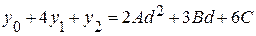 ,
,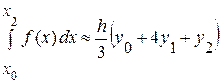 (I.5)
(I.5)
 (I.6)
(I.6)

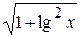
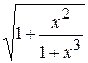
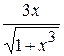
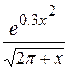
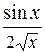
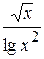

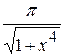
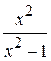


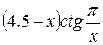


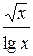
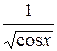


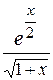

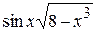
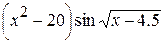

 , (2.1)
, (2.1)







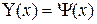 , где
, где  и
и 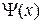 более простые функции, нежели f(x).
более простые функции, нежели f(x).
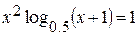 .
. .
.




 .
. методом итераций состоит в выборе начального приближения значения x0 и последовательном вычислении
методом итераций состоит в выборе начального приближения значения x0 и последовательном вычислении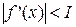 , то последовательность xi сходится к исходному корню.
, то последовательность xi сходится к исходному корню. .
. и N задаются.
и N задаются.





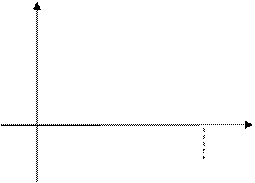



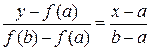 .
.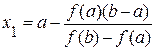 .
. ,
, и т.д.
и т.д. (2.2)
(2.2)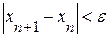 , где
, где 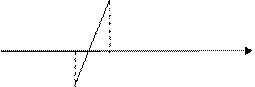


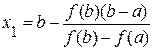 .
.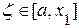 . Применяя метод хорд к отрезку, получим
. Применяя метод хорд к отрезку, получим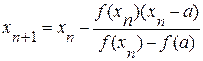 (2.3)
(2.3)
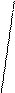
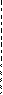


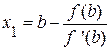 .
. , получим
, получим  .
. (2.4)
(2.4)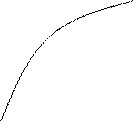


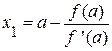 .
. . необходимо вычислить
. необходимо вычислить 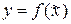 .
.


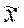
 и
и  , имеет вид:
, имеет вид: 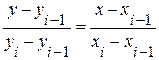 , т.е.
, т.е.  .
. возьмем
возьмем  .
.
 , где f – известная функция;
, где f – известная функция;  - неизвестные постоянные параметры, значения которых надо найти.
- неизвестные постоянные параметры, значения которых надо найти. ,
, 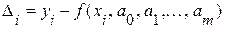 .
.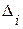 - назовем отклонениями. Поскольку
- назовем отклонениями. Поскольку  и
и  , вообще говоря, не совпадают все или некоторые
, вообще говоря, не совпадают все или некоторые 


