
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Математическая постановка задачи интерполированияСодержание книги
Поиск на нашем сайте
Пусть на отрезке [x0, xn] задана функция y=f(x) своими n+1 значениями. y0=f(x0), y1=f(x1), …, yn=f(xn) в точках x0, x1, …, xn, которые назовем узлами интерполяции. Предполагается, что при
которая в узлах интерполяции совпадает со значениями заданной функции, т.е. y0=Y(x0), y1=Y(x1), …, yn=Y(xn) Процесс вычисления значений функции в точках x, отличных от узлов интерполяции, называют интерполированием функции f(x). Если аргумент x, для которого определяется приближенное значение функции Геометрически задача интерполирования для функции одной переменой y=f(x) означает построение кривой, проходящей через точки плоскости с координатами (x0, y0), (x1, y1), …, (xn, yn) (рис. 3.1) следующие формулы для уточнения корня уравнения:
 
Рис. 3.1
Очевидно, что через данные точки можно провести бесконечно много кривых. Таким образом, задача отыскания функции Y(x) по конечному числу ее значений является неопределенной. Но если в качестве интерполирующей функции Y(x) взять многочлен степени не выше nYn(x), то задача станет однозначной.
Интерполяционный многочлен Лагранжа
Пусть функция задана таблично
Построим многочлен Ln(x), такой, что Ln(x0)= y0, Ln(x1)= y1, …, Ln(xn)= yn. (3.1) При такой постановке задачи узлы интерполяции x0, x1, …, xn могут произвольно отстоять друг от друга, т.е. узлы интерполяции неравноотстоящие. Задача имеет решение, если степень многочлена Ln(x) будет не выше n. Представим многочлен Ln(x) в виде:
где ai (i=0,1,…,n) неизвестные коэффициенты, которые надо найти. Из условий (3.1) следует, что
Таким образом, получаем систему из n+1 уравнение для нахождения (n+1) неизвестных a0, a1, …, an
определитель которой
Тогда существует единственное решение этой системы
Найдя коэффициенты a0, a1, …, an, запишем многочлен Ln(x). Однако, каждый раз решать систему уравнений (3.2) затруднительно, поэтому рассмотрим другой способ построения Ln(x). Запишем его в виде:
Из выражения (4.3) следует, что функция Qn(x) должна удовлетворять условиям:
Легко видеть, что этим условиям отвечает многочлен вида:
В точках Тогда, подставляя в (3.3) выражение (3.4), окончательно получим:
Этот многочлен называется интерполяционным многочленом Лагранжа. В сокращенном виде его можно записать так:
Линейная интерполяция
В тех случаях, когда нет необходимости в отыскании приближенного выражения функции y=f(x), заданной таблично, можно использовать линейную интерполяцию, которая состоит в следующем. Отыскивается интервал [xi+1, xi], в который попадает значение На отрезке [xi-1, xi] заменим дугу кривой y=f(x) стягивающей ее хордой MN (рис. 2.3).

Рис. 3.2 Уравнение прямой, проходящей через точки В качестве приближенного значения функции
Метод наименьших квадратов
При интерполировании основным условием является совпадение значений функции и значений интерполяционного многочлена в узлах интерполяции. Однако при большом количестве узлов интерполяции получается высокая степень многочлена, что затрудняет вычисление. Кроме того, экспериментальные данные, полученные в результате измерений или наблюдений, могут содержать ошибки, которые вызваны несовершенством измерительных приборов, различными случайными факторами. Построение аппроксимирующего многочлена с условием обязательного прохождения его графика через эти экспериментальные точки будет означать повторение ошибок. Поэтому иногда целесообразней строить многочлен, график которого проходит «близко» от заданных точек. Итак, пусть при изучении неизвестной функциональной зависимости y от x получена таблица значений:
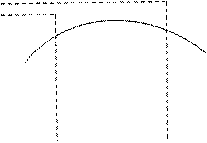
Нужно найти эмпирическую зависимость y=f(x), значение которых при x=xi мало отличались бы от опытных данных yi. График функции y=f(x), вообще говоря, не проходит через точки (xi, yi), как в случае интерполяции, что приводит к сглаживанию экспериментальных данных (рис. 3.3)

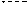 
Рис. 3.3 Построение эмпирической формы состоит из двух этапов: 1) выбор общего вида зависимости; 2) выбор наилучших значений параметров, входящих в формулу. Метод наименьших квадратов не дает возможности выбрать вид зависимости, он позволяет лишь оптимально подобрать параметры приближающей функции. Вид зависимости выбирается из каких-либо дополнительных соображений: физических, геометрических т.д. Будем считать, что тип эмпирической зависимости выбран, и ее можно записать в виде: В каждой точке xi вычислим разность между табличным значением функции yi и вычисленным значением
1) S является функцией от независимых переменных
2) Параметры 3) Минимум найдем, приравнивая к нулю частные производные по этим переменным
Из системы уравнений (3.5) найдем Геометрически (рис. 3.4) метод наименьших квадратов можно интерпретировать так: среди бесконечного множества линий данного вида, проведенных относительно данных экспериментальных точек, выбрать одну, для которой сумма квадратов отклонений будет наименьшей.
приводит к сглаживанию экспериментальных данных (рис. 3.3)

Рис. 3.4
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 610; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.103.70 (0.008 с.) |

 . Требуется найти аналитическое выражение Y(x) функции, заданной таблично.
. Требуется найти аналитическое выражение Y(x) функции, заданной таблично.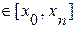 , то задача называется интерполированием в узком смысле. Если x находится за пределами отрезка [x0, xn], то задача отыскания значения функции в точке x называется экстраполированием.
, то задача называется интерполированием в узком смысле. Если x находится за пределами отрезка [x0, xn], то задача отыскания значения функции в точке x называется экстраполированием.


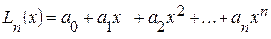 ,
,
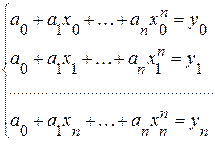 (3.2)
(3.2)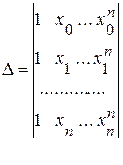 отличен от нуля, если x0, x1, …, xn различны.
отличен от нуля, если x0, x1, …, xn различны.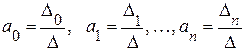 .
.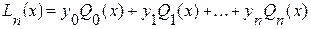 . (3.3)
. (3.3) .
.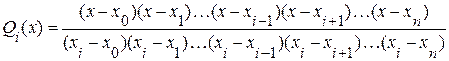 (3.4)
(3.4) функция Qi(x) обращается в 0, а в точке xi равна 1.
функция Qi(x) обращается в 0, а в точке xi равна 1.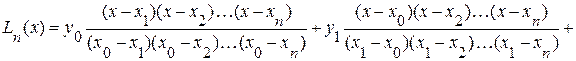
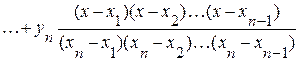 .
.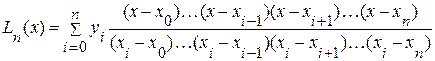 .
. . необходимо вычислить
. необходимо вычислить 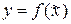 .
.
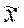
 и
и  , имеет вид:
, имеет вид: 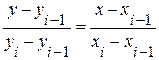 , т.е.
, т.е.  .
. возьмем
возьмем  .
.
 , где f – известная функция;
, где f – известная функция;  - неизвестные постоянные параметры, значения которых надо найти.
- неизвестные постоянные параметры, значения которых надо найти. ,
, 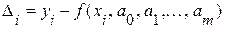 .
.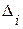 - назовем отклонениями. Поскольку
- назовем отклонениями. Поскольку  и
и  , вообще говоря, не совпадают все или некоторые
, вообще говоря, не совпадают все или некоторые 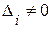 . Запишем сумму квадратов отклонений для всех точек
. Запишем сумму квадратов отклонений для всех точек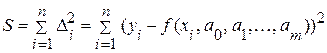 .
.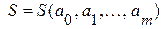
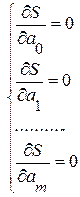 (3.5)
(3.5)








