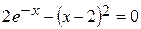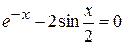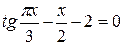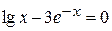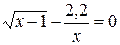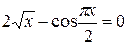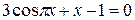Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Комбинированный метод хорд и касательныхСодержание книги
Поиск на нашем сайте
Методы хорд и касательных дают приближения корня с разных сторон. Поэтому их часто применяют в сочетании друг с другом, тогда уточнение корня происходит быстрее. Пусть дано уравнение f(x)=0, корень отделен на отрезке [a, b]. Рассмотрим случай, когда f ‘(x) f ’’(x)>0 (рис. 2.13)
Рис. 2.13 В этом случае метод хорд дает приближенное значение корня с недостатком (конец b неподвижен), а метод касательных – с избытком (за начальное приближение берем точку b). Тогда вычисления следует проводить по формулам:
Теперь корень ξ заключен в интервале [a1, b1]. Применяя к этому отрезку комбинированный метод, получим:
Если же f ‘(x) f ’’(x)<0 (рис. 2.14), то рассуждая аналогично, получим следующие формулы для уточнения корня уравнения:
Рис. 2.14
Вычислительный процесс прекращается, как только
Задания. Найти наименьший положительный корень уравнения одним из методов, указанных преподавателем.
3. АППРОКСИМАЦИЯ ФУНКЦИЙ
Будем считать, что некоторый процесс характеризуется двумя изменяющимися величинами x и y, из которых x выбирается как независимая, а y – как зависимая переменная величина. Предположим, сто каждому значению переменной x соответствует единственное значение переменной y, т.е. y является функцией x. На практике часто известна аналитическая зависимость между x и y, т.е. функцию нельзя записать в виде y=f(x). В некоторых случаях эта зависимость известна, но вычисления значений функций громоздко. В этих случаях прибегают к табличному способу задания функций. Таблица представляет собой набор значений функций для последующих значений аргументов:
Эти значения либо вычислены, либо получены экспериментально. Преимуществом табличного способа задания функций является то, что для каждого значения аргумента, содержащегося в таблице, без вычислений можно найти значение функции. Недостаток этого способа в том, что нельзя составить таблицу для всех значений аргумента, всегда найдутся такие значения аргумента, которых нет в таблице. Таким образом, возникает задача о приближении (аппроксимации) функции: данную функцию y=f(x) требуется приближенно заменить (аппроксимировать) некоторой функцией y(x) так, чтобы отклонения (в некотором смысле) Y(x) от f(x) в заданной области было наименьшим. Функция Y(x) называется аппроксимирующей.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 396; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.237.54 (0.007 с.) |




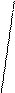



 ;
;  .
. ;
;  и т.д.
и т.д. ;
;  (2.6)
(2.6)



 ;
;  .
.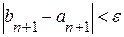 .
.