
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Применение численного интегрирования при решенииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Инженерных задач
Требования к выполнению контрольной работы
Работа содержит одну задачу, вариант которой выдается преподавателем на установочных занятиях. Решение задачи должно содержать следующие разделы: 1. Постановка задачи (приводится условие задачи). 2. Математическая модель задачи. 3. Алгоритм решения задачи. 4. Схема алгоритма решения. 5. Таблица идентификаторов. 6. Текст программы на языке Паскаль. 7. Таблица исходных данных. При организации вычислительного процесса необходимо предусмотреть выполнение следующих действий: 1) очистку экрана; 2) вывод текста – приглашения к вводу; 3) ввод исходных данных; 4) определение приближенного значения интеграла методом трапеций; 5) определение точного значения интеграла по формуле Ньютона-Лейбница. Ниже приведены пояснения к контрольной работе и пример выполнения.
Постановка задачи
Задача численного интегрирования заключается в получении при-ближенного значения Численное интегрирование используется: 1) при задании подынтегральной функции f (x) в виде таблицы:
где x 1 = a, xn +1 = b; 2) при задании подынтегральной функции f (x) в виде графика, полученного, например, опытным путем (рис. 2.1);
Рис. 2.1
3) если аналитическое определение F(x) сложно или невозможно.
Математическая модель задачи
Построим математическую модель приближенного вычисления интеграла Для непрерывной на интервале [ a, b ] функции f (x) величина опре-деленного интеграла
Рис. 2.2
Разобьем отрезок интегрирования [ a, b ] на n равных элементарных участков длиной Каждая i -я точка определяется значением аргумента, которое обозначим xi. Из рис. 2.2 видно, что при i=1 x1=a; i=2 x2=a+h; i=3 x3=a+2h; ... i=i xi=a+(i-1)h; ... i=n+1 В каждой i -й точке вычислим значение подынтегральной функции yi = f(xi). Площадь под кривой y = f(x) на одном из участков разбиения [ xi -1, xi ] равна
Следовательно,
  . .
Тогда (см. рис. 2.2)
 . .
Алгоритм решения задачи
Приведем алгоритм вычисления приближенного значения 1. Исходные данные (ввод): a, b, n 2. 3. i = 1,..., n + 1 3.1. xi = a + (i - 1) × h 3.2. yi = f (xi) 4. Int = 0 5. i = 2,..., n + 1 5.1.
Пример решения задачи
Определить максимальную высоту hmax подъема тела, брошенного вертикально вверх со скоростью vнач, вычислив При вычислении интеграла аргументом является t, подынтегральная функция f (t) = vнач - gt, нижний предел интегрирования tнач = 0. Верхний предел интегрирования tкон вычислим из условия равенства нулю скорости тела в наивысшей точке подъема:
Найдем точное значение интеграла по формуле Ньютона-Лейб-ница:
Для нахождения приближенного значения интеграла hmax методом трапеций используем алгоритм, построенный в пп. 1-5 (разд. 2.2.4). Окончательно алгоритм решения задачи примет вид: 1. Исходные данные (ввод): vнач, tнач, g, n 2. 3. 4. i = 1,..., n + 1 4.1. 4.2. 5. h = 0 6. i = 2,..., n + 1 6.1. 7. 8. Схема алгоритма имеет следующий вид:
Задания к контрольной работе №2
1. Определить длину l кривой от точки xнач = 0 до точки xкон = 1, вычислив 2. Определить работу АД силы FД = s 2 от точки Sнач = 0 до точки Sкон = 3, вычислив 3. Определить работу АД момента МД = M0×sin j при повороте вала от j нач = 0 до j кон = p, вычислив 4. Определить угол поворота механизма j за время от tнач = 0 до tкон = 5c, вычислив 5. Определить угловую скорость w при повороте вала от j нач = 0 до j кон = p, вычислив 6. Определить путь S, пройденный телом за время от tнач = 0 до tкон = 15c, вычислив 7. Определить площадь S, ограниченную кривой y = ex на интервале от точки xнач = 0 до точки xкон = 3, вычислив 8. Определить работу АС силы сопротивления FС = F0 × (1 + 0,5 S) на участке от точки Sнач = 3 до точки Sкон = 5, вычислив 9. Определить реакцию Rn при трении по дуге контакта от b нач = 0 до b кон = p/2, вычислив 10. Определить время t движения при изменении угловой скорости от w нач = 0 до w кон = 10с-1, вычислив
КУРСОВАЯ РАБОТА
Задания на курсовую работу
Студенту предлагается выполнить курсовую работу на одну из тем: 1. Определение параметров поступательного движения тела на плоскости. 2. Определение параметров вращательного движения вала. Исходные данные на проектирование для поступательного движения даны в табл. 3.1, для вращательного движения – в табл. 3.2. Тема курсовой работы и вариант исходных данных сообщаются преподавателем на установочных занятиях. Ниже приведены пояснения к поставленной задаче, требования к пояснительной записке и пример выполнения курсовой работы.
|
|||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 412; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.195.84 (0.007 с.) |

 . Если подынтегральная функция f (x) непрерывна на отрезке [ a, b ] и на нем существует ее первообразная F (x), то по формуле Ньютона-Лейбница
. Если подынтегральная функция f (x) непрерывна на отрезке [ a, b ] и на нем существует ее первообразная F (x), то по формуле Ньютона-Лейбница 
 равна площади, ограниченной кривой y = f(x), осью абсцисс ОХ и прямыми x = a и x = b (рис. 2.2).
равна площади, ограниченной кривой y = f(x), осью абсцисс ОХ и прямыми x = a и x = b (рис. 2.2).
 . Полученные промежуточные точки пронумеруем от 1 до n + 1. Введем переменную i, определяющую номер промежуточной точки.
. Полученные промежуточные точки пронумеруем от 1 до n + 1. Введем переменную i, определяющую номер промежуточной точки. =b.
=b.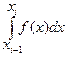 (рис. 2.3).
(рис. 2.3). Эту площадь можно с некоторой погрешностью считать равной площади трапеции и вычислить по формуле
Эту площадь можно с некоторой погрешностью считать равной площади трапеции и вычислить по формуле .
. .
. , где g = 9,81. Получить точное и приближенное значения интеграла.
, где g = 9,81. Получить точное и приближенное значения интеграла. .
. .
.





 .
.

 .
. .
. , где М0 = 25 Нм.
, где М0 = 25 Нм. , где w 0 = 20с-1.
, где w 0 = 20с-1. , где JП = 10 кгм2, М0 = 100 Нм.
, где JП = 10 кгм2, М0 = 100 Нм. , где v 0= 1,2 м/с, а = 0,5 м/с2.
, где v 0= 1,2 м/с, а = 0,5 м/с2.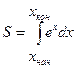 .
. , где F0 = 10 H.
, где F0 = 10 H. , где r = 0,01 м,
, где r = 0,01 м,  , где JП =7,5 кг×м2.
, где JП =7,5 кг×м2.


