
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Математическая модель движенияСодержание книги Поиск на нашем сайте
В произвольном положении на тело массой m действует сила тяжести G = mg и сила сопротивления воздуха Fс = kv. Тогда в соответствии со вторым законом Ньютона дифференциальное уравнение движения в проекции на ось Y запишется, с учетом соотношения
с начальным условием
Ее решение на промежутке времени [ tнач, tкон ] покажет характер изменения скорости тела при полете вверх. Для нахождения максимальной высоты подъема учитываем, что
Разобьем промежуток времени [ tнач, tкон ] на n равных элементарных участков
Количество исследуемых положений тела будет равно n + 1. Каждому i -му положению соответствует время ti, исчисляемое от начала движения, и скорость vi. Зададим для 1-го положения t 1 = tнач = 0,
где
Максимальная высота подъема hmax (см. формулу 3.4.2) определяется путем численного интегрирования по методу трапеций:
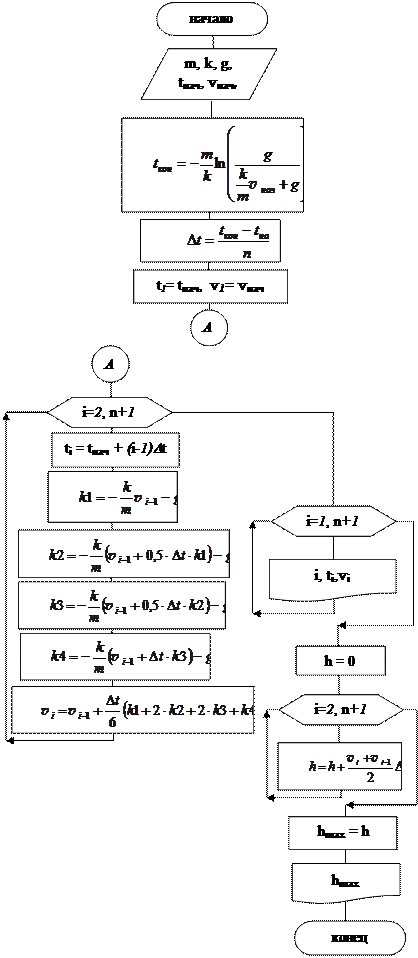
Алгоритм решения
1. Исходные данные (ввод): m, vнач, tнач, k, g, n. 2. 3. 4. t 1 = tнач, v 1 = vнач 5. Для i= 2,...,n+ 1 5.1.ti= tнач+ ( i- 1)D t 5.2. 5.3. 5.4. 5.5. 5.6. 6. h= 0 7. i= 2,...,n +1 7.1. 8. hmax=h
Схема алгоритма решения
Таблица идентификаторов
Текст программы
program kurs_010; {Петров В.И., группа 303010} {Исследование движения тела,} {брошенного вертикально вверх} {Вариант 5} uses crt; type Mas=array[1..201] of real; var v,t:Mas; m,k,v0,g,tn,tk,dt,k1,k2,k3,k4,h,hmax:real; i,n:integer; fu:text; begin clrscr; assign(fu,'kurs_010.rez'); rewrite(fu); writeln(fu,' ':20,'Исследование движения тела,'); writeln(fu,' ':19,'брошенного вертикально вверх'); writeln(fu); writeln(fu,' ':20,'Петров В.И., группа 303010'); writeln(fu); writeln(fu,' ':25,'Вариант 5'); writeln('Введите исходные данные');
write('Масса тела равна m='); readln(m); write('Начальное время tn='); readln(tn); write('Начальная скорость тела v0='); readln(v0); write('Коэффициент сопротивления среды k='); readln(k); write('Ускорение свободного падения g='); readln(g); write('Количество разбиений участка [tn,tk] n='); readln(n); writeln(fu); writeln(fu,' ':15,'Исходные данные:'); writeln(fu); writeln(fu,' ':10,'Масса тела m=',m:5:2,'кг'); writeln(fu,' ':10,'Начальная скорость тела v0=', v0:5:2,'м/c'); writeln(fu,' ':10,'Коэффициент сопротивления среды', ' k=',k:5:2); writeln(fu,' ':10,'Ускорение свободного падения g=', g:3:1,'м/c**2'); writeln(fu,' ':10,'Количество разбиений участка', ' [tn,tk] n=',n:2); tk:=-m/k*ln(g/(k/m*v0+g)); writeln(fu); writeln(fu); writeln(fu,' ':10,'Общее время полета tk=', tk:7:5,'c'); writeln(fu); dt:=(tk-tn)/n; v[1]:=v0; t[1]:=tn; for i:=2 to n+1 do begin t[i]:=tn+(i-1)*dt; k1:=-k/m*v[i-1]-g; k2:=-k/m*(v[i-1]+0.5*dt*k1)-g; k3:=-k/m*(v[i-1]+0.5*dt*k2)-g; k4:=-k/m*(v[i-1]+dt*k3)-g; v[i]:=v[i-1]+dt/6*(k1+2*k2+2*k3+k4); end; writeln(fu,' ':17,'I',' ':9,'I'); writeln(fu,' ':15,'i I t I v '); writeln(fu,' ':17,'I',' ':9,'I'); write(fu,' ':14); for i:=1 to 22 do write(fu,'-'); writeln(fu); for i:=1 to n+1 do writeln(fu,' ':14,i:2,' I ',t[i]:7:3,' I ', v[i]:7:5); h:=0; for i:=2 to n+1 do h:=h+(v[i]+v[i-1])/2*dt; hmax:=h; writeln(fu); writeln(fu,' ':5,'Макcимальная высота полета', ' hmax=',hmax:7:5,'м'); close(fu); writeln('Работа окончена'); repeat until keypressed end.
Распечатка результатов
Исследование движения тела, брошенного вертикально вверх Петров В.И., группа 303010 Вариант 5 Исходные данные: Масса тела m= 0.50кг Начальная скорость тела v0= 5.00м/c Коэффициент сопротивления среды k= 0.20 Ускорение свободного падения g=9.8м/c**2 Количество разбиений участка [tn,tk] n=14 Общее время полета tk=0.46429c I I i I t I v I I ---------------------- 1 I 0.000 I 5.00000 2 I 0.033 I 4.61125 3 I 0.066 I 4.22763 4 I 0.099 I 3.84906 5 I 0.133 I 3.47547 6 I 0.166 I 3.10682 7 I 0.199 I 2.74302 8 I 0.232 I 2.38401 9 I 0.265 I 2.02974 10 I 0.298 I 1.68013 11 I 0.332 I 1.33513 12 I 0.365 I 0.99468 13 I 0.398 I 0.65871 14 I 0.431 I 0.32717 15 I 0.464 I 0.00000 Макcимальная высота полета hmax=1.12501м
Графическое представление результатов
0 0,1 0,2 0,3 0,4 0,5 t, c
Анализ результатов
Анализ результатов показывает: а) скорость v 1 равна начальному значению v 1 = vнач; б) с увеличением времени до tкон = 0,46429с скорость убывает линейно.
Литература
1. Справочное пособие по приближенным методам решения задач высшей математики / Л.И. Бородич, А.И. Герасимович, Н.П. Кеда, И.Н. Мелешко. – Мн.: Выш. школа, 1986.
2. О ф и ц е р о в Д. В., С т а р ы х В. А. Программирование в интегрированной среде Турбо–Паскаль: Справ. пособие. – Мн.: Беларусь, 1992. 3. П е т р о в А. В., Т и т о в М. А., Ш к а т о в П. Н. Вычислительная техника и программирование: Курсовая работа / Под ред. А.В.Петрова. – М.: Высш. школа, 1992.
Рекомендуемая литература 1. А л е к с е е в В. Е., В а у л и н А. С., П е т р о в а Г. Б. Вычислительная техника и программирование: Практикум по программированию / Под ред. А.В.Петрова. – М.: Высш. школа, 1991. 2. Вычислительная техника и программирование: Учебник для техн. вузов / А.В.Петров, В.Е.Алексеев, А.С.Ваулин и др.; Под ред. А.В.Петрова. – М.: Высш. школа, 1990. 3. О ф и ц е р о в Д. В., С т а р ы х В. А. Программирование в интегрированной среде Турбо–Паскаль: Справ. пособие. – Мн.: Беларусь, 1992. 4. П е т р о в А. В., Т и т о в М. А., Ш к а т о в П. Н. Вычислительная техника и программирование: Курсовая работа / Под ред. А.В.Петрова. – М.: Высш. школа, 1992. 5. П о л я к о в Д. Б., К р у г л о в И. Ю. Программирование в среде Турбо–Паскаль: Версия 5.5. – М.: Изд-во МИА, АО «Росвузнаука», 1992. 6. Ф и г у р н о в В. Э. IBM PC для пользователя: Краткий курс. – Сокращенная версия 7-го издания. – М.: ИНФРА, 1999.
Содержание
Учебное издание
Луцко Наталья Яковлевна Анципорович Петр Петрович Булгак Татьяна Ивановна
Информатика.
Контрольные работы и курсовое проектирование
Учебно‑методическое пособие для студентов‑заочников машиностроительных специальностей
Редактор Т.Н.Микулик
Подписано в печать 18.03.2004. Формат 60х84 1/16. Бумага типографская № 2. Печать офсетная. Гарнитура Таймс.
Издатель и полиграфическое исполнение: Белорусский национальный технический университет. Лицензия ЛВ №155 от 30.01.2003. 220013, Минск, проспект Ф.Скорины, 65.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 269; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.106.9 (0.009 с.) |

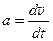 , в виде
, в виде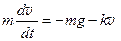
 . Таким образом, математической моделью движения тела, брошенного вертикально вверх, является задача Коши вида
. Таким образом, математической моделью движения тела, брошенного вертикально вверх, является задача Коши вида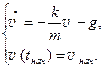 (3.4.1)
(3.4.1)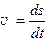 , откуда ds = v × dt. Проинтегрировав это выражение, получим
, откуда ds = v × dt. Проинтегрировав это выражение, получим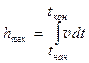 . (3.4.2)
. (3.4.2) .
.
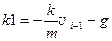 ;
; ;
; ;
; .
. .
.
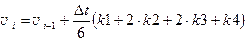
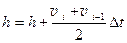


 v, м/c
v, м/c

 Компьютерная верстка Л.М.Чернышевич
Компьютерная верстка Л.М.Чернышевич Усл. печ. л. 4,1. Уч.-изд. л. 3,2. Тираж 500. Заказ 230.
Усл. печ. л. 4,1. Уч.-изд. л. 3,2. Тираж 500. Заказ 230.


