
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Численные методы вычисления определённого интегралаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пусть функция f(x) непрерывна на отрезке [ а; b ]. Если она задана аналитически, и её первообразная F(x) на этом отрезке выражается в элементарных функциях, то вычисление где F(х) – первообразная функция для f(х). Но не для всякой непрерывной функции её первообразная выражается через элементарные функции (имеем так называемый «неберущийся» интеграл). Кроме того, на практике сталкиваются с необходимостью вычислять интегралы от функций, заданных табличным или графическим способами, а также интегралы от функций, первообразные которых выражаются через элементарные функции очень сложно, что требует большой вычислительной работы и с практической точки зрения не рационально. В этих случаях применяются численные методы интегрирования. Основная идея этих методов состоит в том, что подынтегральную функцию f(х) заменяют другой, “близкой” к ней функцией φ(х), первообразная которой находится элементарным образом, а затем приближённо полагают
Так как Пусть на отрезке [ а; b ], а < b, задана непрерывная функция у = f(х) и требуется вычислить a = х1 < x2 < … < xn < xn+1 = b. Длина h каждого из полученных отрезков [ xi, xi+1 ] равна:
Обозначим через уi = f(хi) значения функции у = f(х) в точках разбиения хi: у1=f(х1), у2=f(х2), …, уn=f(хn), уn+1=f(хn+1). В зависимости от того, как аппроксимируют данную функцию f(x) на каждом из отрезков [ xi, xi+1 ], получают различные формулы для приближённого вычисления интеграла а) формулы прямоугольников При вычислении интеграла
Пусть, например, на каждом из отрезков [ xi, xi+1 ] ступенчатая функция принимает значения, равные значению функции f(х) на левом конце этого отрезка, т.е. равные уi (i = 1, 2, …, n).
а) б) Рисунок 4
Таким образом, Если же значения ступенчатой функции на каждом из отрезков [ xi, xi+1 ] совпадают со значением функции на правых концах этих отрезков (рисунок 4,б), то получим формулу:
Формулы (19) и (20) называются формулами прямоугольников. Ясно, что чем меньше шаг разбиения (т.е., чем больше n), тем площадь ступенчатой фигуры ближе к площади криволинейной трапеции, т.е. полученные формулы тем точнее, чем больше n. Иногда, в целях уточнения результата вычислений, за величину Погрешность этих формул может быть оценена следующим образом:
Замечание: в случае возрастающей функции f(x) формулы прямоугольников дают приближённое значение интеграла с недостатком (формула 19) и избытком (формула 20). Для убывающей функции f(х) - все наоборот. б) формула трапеций При вычислении функция f(х) заменяется функцией, график которой представляет собой ломаную линию, соединяющую концы ординат уi и уi+1 (i =1,2,…, n) (рисунок 5).
В этом случае площадь криво- линейной трапеции (следова- тельно, и значение искомого интеграла) считается прибли- жённо равной сумме площадей обычных трапеций с основания- ми уi и уi+1 и высотой
Формула (22) называется формулой трапеций, её погрешность:
в) формула Симпсона В формуле Симпсона (или парабол) части заданной кривой у = f(х) заменяются дугами парабол. В этом случае необходимо, чтобы промежуток интегрирования был разбит на чётное число равных частей (n – чётное).
Тогда справедлива следующая формула для приближенного вычисления определенного интеграла:
Это и есть формула Симпсона, а её погрешность можно оценить так:
Замечание: вычисление погрешностей расчётов по формулам (21), (23) и (25) можно принять только в тех случаях, когда существуют и легко вычисляются (или оцениваются) соответственно производные Пусть, например, интеграл
Отсюда, в частности, при уменьшении шага разбиения вдвое, т.е. Вычитая из первого уравнения второе, находим Следовательно, если мы вычислим по формуле трапеций интеграл Аналогично, для формулы Симпсона эта же погрешность составит
Если задана допустимая погрешность Если же
|
|||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 730; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.155.254 (0.011 с.) |

 сводится к применению формулы Ньютона-Лейбница:
сводится к применению формулы Ньютона-Лейбница: 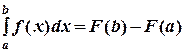 , (16)
, (16) (17)
(17) (18)
(18) Тогда площадь криволинейной трапеции заменяется площадью ступенчатой фигуры, изображённой на рисунке 4, а и считается приближенно равной сумме площадей прямоугольников с высотами уi и основаниями
Тогда площадь криволинейной трапеции заменяется площадью ступенчатой фигуры, изображённой на рисунке 4, а и считается приближенно равной сумме площадей прямоугольников с высотами уi и основаниями  .
.
 (19)
(19)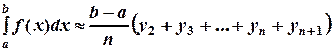 (20)
(20) , где
, где  (21)
(21)
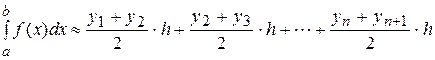 или
или (22)
(22) , где
, где  (23)
(23)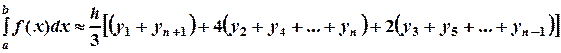 (24)
(24) , где
, где 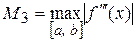 (25)
(25) и
и 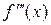 , что на практике встречается, к сожалению, крайне редко. Однако с помощью этих формул можно получить удобные оценки погрешности, которые могут обеспечить надёжные результаты.
, что на практике встречается, к сожалению, крайне редко. Однако с помощью этих формул можно получить удобные оценки погрешности, которые могут обеспечить надёжные результаты. вычислен по формуле трапеций дважды при различных значениях шага разбиения
вычислен по формуле трапеций дважды при различных значениях шага разбиения  ,
,  ,
, 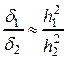 или
или (26)
(26) , получаем
, получаем  . Для точного значения интеграла I при двух вычислениях с шагом
. Для точного значения интеграла I при двух вычислениях с шагом  и
и  ;
;  .
. , или, применяя более общие обозначения, запишем:
, или, применяя более общие обозначения, запишем:  (27)
(27) , разделив отрезок интегрирования [ а; b ] первый раз на n частей, а второй раз – на 2n частей, то для второго результата
, разделив отрезок интегрирования [ а; b ] первый раз на n частей, а второй раз – на 2n частей, то для второго результата  погрешность приблизительно будет равняться
погрешность приблизительно будет равняться 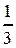 разности результата
разности результата  .
. (28)
(28) , а полученная погрешность
, а полученная погрешность  , то
, то  (29)
(29) , то шаг опять уменьшают вдвое и вычисления повторяют. Указанный способ подсчета погрешностей называют правилом Рунге, а метод нахождения приближённого значения интеграла – методом Рунге, который используется в расчётах на ПК.
, то шаг опять уменьшают вдвое и вычисления повторяют. Указанный способ подсчета погрешностей называют правилом Рунге, а метод нахождения приближённого значения интеграла – методом Рунге, который используется в расчётах на ПК.


