
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Следовательно, данный интеграл сходится.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Задание 2.б Вычислите несобственный интеграл (или установите его расходимость): Решение. Подынтегральная функция f(x) =
Задание 3.а Дан интеграл Найдите: 1) точное значение по формуле Ньютона-Лейбница; 2) приближённое значение (вручную) по формулам прямоугольников, трапеций, Симпсона, разбив отрезок интегрирования на 10 равных частей. Все промежуточные вычисления производите с округлением до четвёртого десятичного знака; 3) сравните полученные результаты с точным значением интеграла, найдя абсолютную и относительную погрешности для каждой из формул; 4) сделайте выводы. Решение. 1) Вычислим данный интеграл, используя метод замены переменной: =
2) Для вычисления интеграла по приближённым формулам разобьём отрезок интегрирования исходного интеграла [15;47] на 10 равных частей (n = 10), тогда шаг разбиения равен: а) Вычислим приближённое значение интеграла по формулам прямоугольников. Для удобства вычислений формулу прямоугольников (19) перепишем в виде: Так как подынтегральная функция убывает на отрезке [15; 47] (что видно по её значениям в таблице 1), то, используя формулу (28), мы получим приближённое значение интеграла с избытком:
Таблица 1 – Значения подынтегральной функции
Абсолютная погрешность ∆ вычислений определяется как разность между точным и приближённым значениями интеграла, взятая по абсолютной величине: Тогда Относительная погрешность δ определяется как отношение абсолютной погрешности к точному значению интеграла в процентах:
Формулу прямоугольников (20) запишем в виде:
Тогда, приближённое значение интеграла с недостатком. Абсолютная и относительная погрешности вычислений по этой формуле составляют: Для получения более точного значения данного интеграла можно взять среднее арифметическое значений полученных по формулам прямоугольников: б) Вычислим приближённое значение интеграла, используя формулу трапеций (22), которую перепишем в виде:
Тогда для данного интеграла приближённое значение, найденное по формуле (32) равно:
Абсолютная и относительная погрешности равны:
в) Вычислим приближённое значение интеграла по формуле Симпсона (24), которую запишем в виде:
Для данного интеграла получаем:
Абсолютная и относительная погрешности от применения формулы Симпсона равны нулю. Сравнивая полученные результаты, можно сделать вывод, что формула Симпсона даёт наилучшее приближение к точному значению интеграла, т.к. относительная погрешность при её применении – наименьшая.
Задание 3.б Вычислить приближённое значение интеграла с использованием Mathcad: Решение. Mathcad – программное средство, среда для выполнения на компьютере разнообразных математических и технических расчётов. Основное отличие Mathcad от других программных средств этого класса состоит в том, что математические выражения на экране компьютера представлены в общепринятой математической нотации – имеют точно такой вид, как в книге, тетради или на доске.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 616; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.008 с.) |


 непрерывна в своей области определения, то есть при всех х, кроме х = 0, в которой она терпит разрыв второго рода. Согласно формуле (15) имеем:
непрерывна в своей области определения, то есть при всех х, кроме х = 0, в которой она терпит разрыв второго рода. Согласно формуле (15) имеем: 


 интеграл расходится.
интеграл расходится. .
. =
= . Подынтегральная дробь является неправильной рациональной дробью (так как в числителе и знаменателе находятся многочлены одинаковой степени, равной единице), в которой следует выделить целую часть. Это можно сделать двумя способами: делением «уголком» многочлена, стоящего в числителе, на знаменатель или искусственно выделяя в числителе такое же выражение, что и знаменатель. Применим в данной задаче второй способ:
. Подынтегральная дробь является неправильной рациональной дробью (так как в числителе и знаменателе находятся многочлены одинаковой степени, равной единице), в которой следует выделить целую часть. Это можно сделать двумя способами: делением «уголком» многочлена, стоящего в числителе, на знаменатель или искусственно выделяя в числителе такое же выражение, что и знаменатель. Применим в данной задаче второй способ:
 . При этом точки деления xi находятся путём прибавления к предыдущему значению шага разбиения: xi+1 =xi + h, где i =1,2,..,10, x1 = a. Запишем найденные значения во второй столбец таблицы 1. В точках деления xi определим соответствующие значения подынтегральной функции
. При этом точки деления xi находятся путём прибавления к предыдущему значению шага разбиения: xi+1 =xi + h, где i =1,2,..,10, x1 = a. Запишем найденные значения во второй столбец таблицы 1. В точках деления xi определим соответствующие значения подынтегральной функции 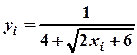 , и занесём их в таблицу 1, выделяя в ней столбцы значений функции с чётными и нечётными индексами.
, и занесём их в таблицу 1, выделяя в ней столбцы значений функции с чётными и нечётными индексами. (28)
(28)
 (29)
(29) .
. (30)
(30) .
. (31)
(31) ,
, ,
,  .
.
 (32)
(32) .
. ,
,  .
. (33)
(33) .
.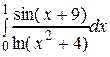 .
.


