
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
К выполнению расчётно-графической работыСтр 1 из 6Следующая ⇒
Кафедра математики
ОПРЕДЕЛЁННЫЕ ИНТЕГРАЛЫ И ИХ ПРИЛОЖЕНИЯ Методические указания К выполнению расчётно-графической работы (для студентов всех направлений)
Новочеркасск
Министерство сельского хозяйства Российской Федерации
высшего профессионального образования «НОВОЧЕРКАССКАЯ ГОСУДАРСТВЕННАЯ МЕЛИОРАТИВНАЯ КАДЕМИЯ»
Кафедра математики
ОПРЕДЕЛЁННЫЕ ИНТЕГРАЛЫ И ИХ ПРИЛОЖЕНИЯ
Методические указания
Новочеркасск
Р 598
Методические указания составлены зав. каф. математики, канд. техн. наук Рогозиной Ю.С. и доцентом каф. математики Кузнецовой М.В.
Рецензенты: Дьяченко В.Б., канд. техн. наук, профессор, зав. каф. информатики ФГБОУ ВПО НГМА Башняк И.М., канд.техн. наук, доц. каф. математики ФГБОУ ВПО НГМА
Рогозина, Ю.С. Р 598 Определённые интегралы и их приложения: [Текст]: метод. указ. к выполнению расчётно-графической работы для студ. всех направлений / Ю.С. Рогозина, М.В. Кузнецова; Новочерк. гос. мелиор. акад., каф. мат-ки - Новочеркасск, 2012. – 31с.
Методические указания предназначены студентам I курса очной формы обучения всех направлений НГМА для организации их самостоятельной работы при выполнении расчётно-графической работы по теме «Определённые интегралы и их приложения» в курсах дисциплин: «Математика», «Высшая математика», «Математический анализ». Ключевые слова: определённый интеграл, площадь, объём тела вращения, несобственные интегралы, численное интегрирование.
Оглавление
с 1 КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ……………………………….4 1.1 Геометрические приложения определённого интеграла………………4 1.2 Вычисление несобственных интегралов (или установление их расходимости)……………………………………………………………6 1.3 Численные методы вычисления определённого интеграла…………...7 2 ОБРАЗЕЦ ВЫПОЛНЕНИЯ РАСЧЁТНО-ГРАФИЧЕСКОЙ РАБОТЫ.....12 3 ВАРИАНТЫ ЗАДАНИЙ ДЛЯ ВЫПОЛНЕНИЯ РАСЧЁТНО- ГРАФИЧЕСКОЙ РАБОТЫ………………………………………………...21 ПРИЛОЖЕНИЕ. Контрольные вопросы для защиты РГР…..……………..29
ЛИТЕРАТУРА ………………………………….…………………………….30
Данное пособие предназначено для студентов I курсов всех направлений при выполнении ими расчётно-графической работы (РГР) по теме: «Определённые интегралы и их приложения». Расчётно-графическая работа содержит 3 задания: 1. Геометрические приложения определённого интеграла: а) вычисление площадей плоских фигур; б) вычисление объёмов тел вращения. Вычисление несобственных интегралов (или установление их расходимости). Численные методы вычисления определённого интеграла. При выполнении третьего задания предполагается один из примеров решать с применением пакета Mathcad на персональном компьютере. Перед выполнением РГР необходимо изучить теоретический материал, используя литературу [1-4], а также конспекты лекций. При решении задач требуется обосновывать каждый этап решения, исходя из теоретических положений курса. Вычисления следует располагать в строгом порядке, отделяя вспомогательные вычисления от основных. Чертежи можно выполнять от руки, но на миллиметровой бумаге, аккуратно и в соответствии с данными условиями, указывая оси, масштаб. При защите РГР необходимо уметь отвечать на контрольные вопросы, которые приведены в приложении.
КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
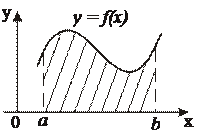
Геометрические приложения определённого интеграла а) вычисление площадей плоских фигур Исходя из геометрического смысла определенного интеграла, площадь фигуры, ограниченной графиком непрерывной функции у = f(х) (f(х) ≥ 0), двумя прямыми х = а и х = b, параллельными оси Оу и отрезком [ а; b ] оси Ох, или площадь криволинейной трапеции (рисунок 1,а), вычисляется по формуле:
а) б) в) Рисунок 1
Если f(х) ≤ 0 на отрезке [ а; b ] (рисунок 1,б), то площадь фигуры, ограниченной дугой графика у = f(х), а ≤ х ≤ b вычисляется по формуле:
В случае, когда фигура ограничена графиком непрерывной функции х = φ(у), (φ(у) ≥ 0), двумя прямыми х = с, х = d, параллельными оси Ох и отрезком [ с; d ] оси Оу (рисунок 1, в), её площадь вычисляется по формуле:
Площадь фигуры, ограниченной графиками непрерывных функций у=f1(х) и у=f2(х), причем f1(х) ≤ f2(х) на отрезке [ а; b ], и двумя прямыми х= а, х =b (рисунок 2, а), вычисляется по формуле:
а) б) в) Рисунок 2
Аналогично, площадь фигуры, изображённой на рисунке 2, б, вычисляется по формуле: Для фигуры, изображенной на рисунке 2, в, площадь следует определять как сумму площадей S1 и S2, для каждой из которых применяем формулу (1):
б) вычисление объёмов тел вращения Если криволинейная трапеция, ограниченная кривой у = f(х), а ≤ х ≤ b, вращается вокруг оси Ох (рисунок 3, а), то объём тела вращения вычисляется по формуле:
а) б) в) Рисунок 3
Аналогично, при вращении криволинейной трапеции ограниченной кривой х = φ(у), с ≤ у ≤ d, вокруг оси Оу (рисунок 3, б), объём тела вращения вычисляется по формуле: Если фигура, ограниченная графиками непрерывных функций у=f1(х) и у=f2(х), f1(х) ≤ f2(х) на отрезке [ а; b ], и двумя прямыми х= а, х =b (рисунок 3, в), вращается вокруг оси Ох, то объём тела вращения вычисляется по формуле:
Расходимости) а) интегралы с бесконечными пределами Если функция f(х) непрерывна при а ≤ х < + ∞, то по определению:
Интеграл, стоящий в левой части формулы (10) называется несобственным. Если существует конечный предел в правой части формулы (10), то несобственный интеграл называется сходящимся, если этот предел не существует или бесконечен, то – расходящимся. Геометрически несобственный интеграл (10) в случае,когда f(х) > 0, есть площадь фигуры, ограниченной графиком функции у = f(х), прямой х = а и осью Ох (асимптотой). Аналогично, определяются интегралы
где с – произвольное число (обычно с = 0). При этом несобственный интеграл (12) сходится, если существуют и конечны оба предела, стоящие в правой части формулы (12). Если хотя бы один из них не существует или бесконечен, то несобственный интеграл расходится. б) интегралы от неограниченных функций Если функция f(x) непрерывна при а ≤ х < b и f(b) = ∞ (терпит разрыв второго рода при х = b), то по определению:
Если существует конечный предел в правой части формулы (13), то несобственный интеграл называется сходящимся, если этот предел не существует или бесконечен, то – расходящимся. Геометрически несобственный интеграл (13) в случае f(x) > 0 есть площадь фигуры, ограниченной графиком функции у=f(х), прямой х = а и вертикальной асимптотой х = b. Аналогично определяется несобственный интеграл в случае, когда f(a) = ∞ (f(x) терпит разрыв второго рода при х = а):
В случае, когда с Î (а; b) – точка разрыва второго рода для f(x) (т.е. f(с) = ∞), несобственный интеграл определяется следующим образом:
При этом несобственный интеграл (15) сходится, если существуют и конечны оба предела, стоящие в правой части формулы (15). Если хотя бы один из них не существует или бесконечен, то несобственный интеграл расходится.
Рисунок 4
Таким образом, Если же значения ступенчатой функции на каждом из отрезков [ xi, xi+1 ] совпадают со значением функции на правых концах этих отрезков (рисунок 4,б), то получим формулу:
Формулы (19) и (20) называются формулами прямоугольников. Ясно, что чем меньше шаг разбиения (т.е., чем больше n), тем площадь ступенчатой фигуры ближе к площади криволинейной трапеции, т.е. полученные формулы тем точнее, чем больше n. Иногда, в целях уточнения результата вычислений, за величину Погрешность этих формул может быть оценена следующим образом:
Замечание: в случае возрастающей функции f(x) формулы прямоугольников дают приближённое значение интеграла с недостатком (формула 19) и избытком (формула 20). Для убывающей функции f(х) - все наоборот. б) формула трапеций При вычислении функция f(х) заменяется функцией, график которой представляет собой ломаную линию, соединяющую концы ординат уi и уi+1 (i =1,2,…, n) (рисунок 5).
В этом случае площадь криво- линейной трапеции (следова- тельно, и значение искомого интеграла) считается прибли- жённо равной сумме площадей обычных трапеций с основания- ми уi и уi+1 и высотой
Формула (22) называется формулой трапеций, её погрешность:
в) формула Симпсона В формуле Симпсона (или парабол) части заданной кривой у = f(х) заменяются дугами парабол. В этом случае необходимо, чтобы промежуток интегрирования был разбит на чётное число равных частей (n – чётное). Тогда справедлива следующая формула для приближенного вычисления определенного интеграла:
Это и есть формула Симпсона, а её погрешность можно оценить так:
Замечание: вычисление погрешностей расчётов по формулам (21), (23) и (25) можно принять только в тех случаях, когда существуют и легко вычисляются (или оцениваются) соответственно производные Пусть, например, интеграл
Отсюда, в частности, при уменьшении шага разбиения вдвое, т.е.
Вычитая из первого уравнения второе, находим Следовательно, если мы вычислим по формуле трапеций интеграл Аналогично, для формулы Симпсона эта же погрешность составит
Если задана допустимая погрешность Если же
Работы Задание 1.а Вычислите площадь плоской фигуры, ограниченной линиями, которые заданы уравнениями: 2х2 – 4х + у = 0, 2х – у – 4 = 0. Сделайте чертёж. Решение. 1) Для вычисления площади заданной фигуры сначала построим её. Первая линия, определяемая уравнением 2х2–4х+у=0 или у = 4х – 2х2, является параболой, заданной трёхчленным уравнением вида у = ах2 + bх +с, ось симметрии которой параллельна оси Оy. Так как коэффициент a = -2< 0, то ветви параболы направлены вниз. Координаты вершина параболы находятся по формулам:
Найдём точки пересечения параболы с осями координат. С осью Ox: у = 0 Þ 4х – 2х2 = 0 Þ 2х(2 - х) = 0 Þ Þ х1 = 0; х2 = 2; с осью Oy: х = 0 Þ у = 0. Строим параболу (рисунок 6). Вторая линия, определяемая уравнением 2х – у – 4 = 0 – прямая. Для построения прямой найдем её точки пересечения
Строим прямую (рисунок 6). Заштрихованная область, Рисунок 6 Таблица 1 – Значения подынтегральной функции
Абсолютная погрешность ∆ вычислений определяется как разность между точным и приближённым значениями интеграла, взятая по абсолютной величине: Тогда Относительная погрешность δ определяется как отношение абсолютной погрешности к точному значению интеграла в процентах:
Формулу прямоугольников (20) запишем в виде:
Тогда, приближённое значение интеграла с недостатком. Абсолютная и относительная погрешности вычислений по этой формуле составляют: Для получения более точного значения данного интеграла можно взять среднее арифметическое значений полученных по формулам прямоугольников: б) Вычислим приближённое значение интеграла, используя формулу трапеций (22), которую перепишем в виде:
Тогда для данного интеграла приближённое значение, найденное по формуле (32) равно:
Абсолютная и относительная погрешности равны:
в) Вычислим приближённое значение интеграла по формуле Симпсона (24), которую запишем в виде:
Для данного интеграла получаем:
Абсолютная и относительная погрешности от применения формулы Симпсона равны нулю. Сравнивая полученные результаты, можно сделать вывод, что формула Симпсона даёт наилучшее приближение к точному значению интеграла, т.к. относительная погрешность при её применении – наименьшая.
Задание 3.б Вычислить приближённое значение интеграла с использованием Mathcad: Решение. Mathcad – программное средство, среда для выполнения на компьютере разнообразных математических и технических расчётов. Основное отличие Mathcad от других программных средств этого класса состоит в том, что математические выражения на экране компьютера представлены в общепринятой математической нотации – имеют точно такой вид, как в книге, тетради или на доске. Варианты заданий для выполнения ПРИЛОЖЕНИЕ Контрольные вопросы для защиты РГР 1. Какая функция называется первообразной для f(х)? Сколько первообразных можно указать для f(х)? 2. Что называется неопределённым интегралом? Каков его геометрический смысл? 3. Какими свойствами обладает неопределённый интеграл? 4. Что называется n -ой интегральной суммой для функции f(х) на отрезке [ а; b ]? 5. Что называется определённым интегралом от функции f(х) на отрезке [ а; b ]? Всегда ли он существует? 6. Какими свойствами обладает определённый интеграл? 7. Каковы геометрический и механический смыслы определенного интеграла? 8. Как вычисляют определенный интеграл по формуле Ньютона-Лейбница? 9. Запишите формулу интегрирования по частям в определённом интеграле. В каких случаях ее применяют? 10. Как осуществляется замена переменной в определённом интеграле? 11. Запишите формулы для вычисления площадей следующих фигур:
а) б) в) г) 12. Как определяется объём тела вращения вокруг оси Ох?; вокруг оси Оу? 13. Как определяются несобственные интегралы с бесконечными пределами? Каков их геометрический смысл? 14. Как определяются несобственные интегралы от разрывных функций? Каков их геометрический смысл? 15. Когда несобственный интеграл сходится?; расходится? 16. На чем основана идея применения приближённых методов интегрирования? 17. Запишите формулы приближённого вычисления определённого интеграла: а) прямоугольников; б) трапеций; в) Симпсона. 18. Как осуществляется приближённое вычисление определённого интеграла с заданной точностью по правилу Рунге?
ЛИТЕРАТУРА
1. Богомолов, Н.В. Практические занятия по математике. Учебное пособие для бакалавров / Н.В. Богомолов. – М.: Юрайт, 2012. – 495с. 2. Кремер, Н.Ш. Высшая математика для экономистов: практикум для студ. вузов,обуч. по экон. спец. / Н.Ш. Кремер [и др.]; под ред. Н.Ш Кремера. – 2-е изд., перераб. и доп. – М.: ЮНИТИ, 2010. – 478 с.(25 экз.) 3. Пискунов, Н.С. Дифференциальное и интегральное исчисление. В 2 т. Т.1: Учеб. пособие для студ. техн. вузов. - М.: Интеграл-Пресс, 2005. – 415 с. (200) 4. Щипачев, В.С. Высшая математика. Полный курс. Учебник для бакалавров / В.С. Щипачев. – М.: Юрайт, 2012. – 607с.
Учебно-методическое издание
Рогозина Юлия Сергеевна Кузнецова Мария Владимировна
ОПРЕДЕЛЁННЫЕ ИНТЕГРАЛЫ И ИХ ПРИЛОЖЕНИЯ Методические указания Кафедра математики
ОПРЕДЕЛЁННЫЕ ИНТЕГРАЛЫ И ИХ ПРИЛОЖЕНИЯ Методические указания к выполнению расчётно-графической работы (для студентов всех направлений)
Новочеркасск
Министерство сельского хозяйства Российской Федерации
высшего профессионального образования «НОВОЧЕРКАССКАЯ ГОСУДАРСТВЕННАЯ МЕЛИОРАТИВНАЯ КАДЕМИЯ»
Кафедра математики
ОПРЕДЕЛЁННЫЕ ИНТЕГРАЛЫ И ИХ ПРИЛОЖЕНИЯ
Методические указания
Новочеркасск
Р 598
Методические указания составлены зав. каф. математики, канд. техн. наук Рогозиной Ю.С. и доцентом каф. математики Кузнецовой М.В.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 352; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.15.15 (0.155 с.) |
 Федеральное государственное бюджетное образовательное учреждение
Федеральное государственное бюджетное образовательное учреждение
 УДК 517.38
УДК 517.38
 (1)
(1)


 (2)
(2) (3)
(3)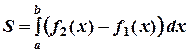 (4)
(4)


 (5)
(5) (6)
(6) (7)
(7)


 (8)
(8) (9)
(9)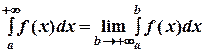 (10)
(10) и
и 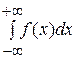 :
: (11)
(11)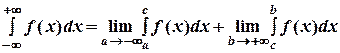 , (12)
, (12) (13)
(13) (14)
(14) (15)
(15) (19)
(19)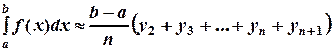 (20)
(20) принимают среднее арифметическое значений, полученных по формулам (19) и (20).
принимают среднее арифметическое значений, полученных по формулам (19) и (20). , где
, где  (21)
(21)
 . Рисунок 5
. Рисунок 5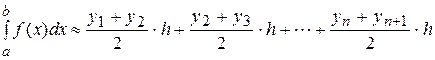 или
или (22)
(22) , где
, где  (23)
(23)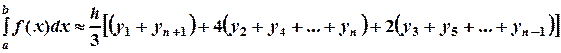 (24)
(24) , где
, где 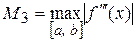 (25)
(25) и
и 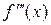 , что на практике встречается, к сожалению, крайне редко. Однако с помощью этих формул можно получить удобные оценки погрешности, которые могут обеспечить надёжные результаты.
, что на практике встречается, к сожалению, крайне редко. Однако с помощью этих формул можно получить удобные оценки погрешности, которые могут обеспечить надёжные результаты. вычислен по формуле трапеций дважды при различных значениях шага разбиения
вычислен по формуле трапеций дважды при различных значениях шага разбиения  ,
,  ,
, 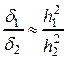 или
или (26)
(26) , получаем
, получаем  . Для точного значения интеграла I при двух вычислениях с шагом
. Для точного значения интеграла I при двух вычислениях с шагом  и
и  ;
;  .
. , или, применяя более общие обозначения, запишем:
, или, применяя более общие обозначения, запишем:  (27)
(27) , разделив отрезок интегрирования [ а; b ] первый раз на n частей, а второй раз – на 2n частей, то для второго результата
, разделив отрезок интегрирования [ а; b ] первый раз на n частей, а второй раз – на 2n частей, то для второго результата  погрешность приблизительно будет равняться
погрешность приблизительно будет равняться 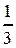 разности результата
разности результата  .
. (28)
(28) , а полученная погрешность
, а полученная погрешность  , то
, то  (29)
(29) , то шаг опять уменьшают вдвое и вычисления повторяют. Указанный способ подсчета погрешностей называют правилом Рунге, а метод нахождения приближённого значения интеграла – методом Рунге, который используется в расчётах на ПК.
, то шаг опять уменьшают вдвое и вычисления повторяют. Указанный способ подсчета погрешностей называют правилом Рунге, а метод нахождения приближённого значения интеграла – методом Рунге, который используется в расчётах на ПК. ,
,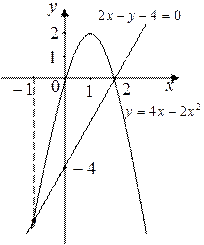 у = у(x0 ) =y (1)=4 – 2=2. Следовательно, вершина находится в точке с координатами (1; 2).
у = у(x0 ) =y (1)=4 – 2=2. Следовательно, вершина находится в точке с координатами (1; 2). с осями координат:
с осями координат: 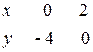 .
. (29)
(29) .
. (30)
(30) .
. (31)
(31) ,
, ,
,  .
.
 (32)
(32) .
. ,
,  .
. (33)
(33) .
.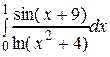 .
.



