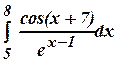Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
расчётно – графической работыСодержание книги
Поиск на нашем сайте
Задание 1. Геометрические приложения определённого интеграла. а) Вычислите площадь плоской фигуры, ограниченной линиями, которые заданы уравнениями. Сделайте чертёж. б) Вычислите объём тела, образованного вращением вокруг координатной оси (в вариантах с нечётными номерами вращение происходит вокруг оси Оу, с чётными – вокруг оси Ох) плоской фигуры, ограниченной линиями, которые заданы соответствующими уравнениями. Сделайте чертёж.
1.1 а) 1.2 а) 1.3 а) 1.4 а) 1.5 а) 1.6 а) 1.7 а) 1.8 а) 1.9 а) 1.10 а) 1.11 а) 1.12 а) 1.13 а) 1.14 а) 1.15 а) 1.16 а) 1.17 а) 1.19 а) 1.21 а) 1.23 а) 1.25 а) 1.27 а) 1.29 а) 1.31 а) 1.32 а) 1.33 а) 1.34 а) 1.35 а) 1.36 а) 1.37 а) 1.38 а) 1.39 а) 1.39 а) 1.40 а) 1.41 а) 1.42 а) 1.43 а) 1.44 а) 1.45 а) 1.46 а) 1.47 а) 1.48 а) 1.49 а) 1.50 а)
Задание 2. Несобственные интегралы Вычислите несобственные интегралы (или установите их расходимость).
2.1 а) б) 2.4 а) б) 2.7 а) б) 2.10 а) б) 2.13 а) б) 2.16 а) б) 2.19 а) б)
2.22 а) б) 2.25 а) б) 2.28 а) б) 2.31 а) б) 2.34 а) б) 2.37 а) б) 2.40 а) б) 2.43 а) б) 2.46 а) б) 2.49 а) б)
Задание 3. Численные методы вычисления определённого интеграла а) Дан интеграл Найдите: 1) точное значение; 2) приближённое значение (вручную) по формулам прямоугольников, трапеций, Симпсона, разбив отрезок интегрирования на 10 равных частей. Все промежуточные вычисления производите с округлением до четвертого десятичного знака; 3) сравните полученные результаты с точным значением интеграла, найдя абсолютную и относительную погрешности для каждой из формул; сделайте выводы. б) Дан интеграл
3.1 а) б) 3.4 а) б) 3.7 а) б) 3.10 а) б) 3.13 а) б) 3.16 а) б) 3.19 а) б) 3.22 а) б) 3.25 а) б) 3.28 а) б) 3.31 а) б) 3.34 а) б) 3.37 а) б) 3.40 а) б) 3.43 а) б) 3.46 а) б) 3.49 а) б) ПРИЛОЖЕНИЕ Контрольные вопросы для защиты РГР 1. Какая функция называется первообразной для f(х)? Сколько первообразных можно указать для f(х)? 2. Что называется неопределённым интегралом? Каков его геометрический смысл? 3. Какими свойствами обладает неопределённый интеграл? 4. Что называется n -ой интегральной суммой для функции f(х) на отрезке [ а; b ]? 5. Что называется определённым интегралом от функции f(х) на отрезке [ а; b ]? Всегда ли он существует? 6. Какими свойствами обладает определённый интеграл? 7. Каковы геометрический и механический смыслы определенного интеграла? 8. Как вычисляют определенный интеграл по формуле Ньютона-Лейбница? 9. Запишите формулу интегрирования по частям в определённом интеграле. В каких случаях ее применяют? 10. Как осуществляется замена переменной в определённом интеграле? 11. Запишите формулы для вычисления площадей следующих фигур:
а) б) в) г) 12. Как определяется объём тела вращения вокруг оси Ох?; вокруг оси Оу? 13. Как определяются несобственные интегралы с бесконечными пределами? Каков их геометрический смысл? 14. Как определяются несобственные интегралы от разрывных функций? Каков их геометрический смысл? 15. Когда несобственный интеграл сходится?; расходится? 16. На чем основана идея применения приближённых методов интегрирования? 17. Запишите формулы приближённого вычисления определённого интеграла: а) прямоугольников; б) трапеций; в) Симпсона. 18. Как осуществляется приближённое вычисление определённого интеграла с заданной точностью по правилу Рунге?
ЛИТЕРАТУРА
1. Богомолов, Н.В. Практические занятия по математике. Учебное пособие для бакалавров / Н.В. Богомолов. – М.: Юрайт, 2012. – 495с. 2. Кремер, Н.Ш. Высшая математика для экономистов: практикум для студ. вузов,обуч. по экон. спец. / Н.Ш. Кремер [и др.]; под ред. Н.Ш Кремера. – 2-е изд., перераб. и доп. – М.: ЮНИТИ, 2010. – 478 с.(25 экз.) 3. Пискунов, Н.С. Дифференциальное и интегральное исчисление. В 2 т. Т.1: Учеб. пособие для студ. техн. вузов. - М.: Интеграл-Пресс, 2005. – 415 с. (200) 4. Щипачев, В.С. Высшая математика. Полный курс. Учебник для бакалавров / В.С. Щипачев. – М.: Юрайт, 2012. – 607с.
Учебно-методическое издание
Рогозина Юлия Сергеевна Кузнецова Мария Владимировна
ОПРЕДЕЛЁННЫЕ ИНТЕГРАЛЫ И ИХ ПРИЛОЖЕНИЯ Методические указания К выполнению расчётно-графической работы (для студентов всех направлений)
Подписано к печати Формат 60×84 1/16 Объем Тираж Заказ
Отдел оперативной полиграфии ФГБОУ ВПО НГМА, 346428, г. Новочеркасск, ул. Пушкинская, 111
|
|||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 238; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.173.197 (0.007 с.) |

 ; б)
; б) 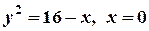
 ; б)
; б) 
 ; б)
; б) 
 ; б)
; б) 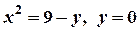
 ; б)
; б) 
 ; б)
; б) 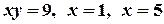
 ; б)
; б) 
 ; б)
; б) 
 ; б)
; б) 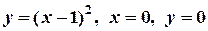
 ; б)
; б) 
 ; б)
; б) 
 ; б)
; б) 
 ; б)
; б) 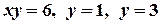
 ; б)
; б) 
 ; б)
; б) 
 ; б)
; б) 
 ; б)
; б)  1.18 а)
1.18 а)  ; б)
; б) 
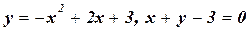 ; б)
; б) 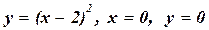 1.20 а)
1.20 а)  ; б)
; б) 
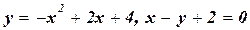 ; б)
; б)  1.22 а)
1.22 а)  ; б)
; б) 
 ; б)
; б) 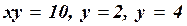 1.24 а)
1.24 а)  ; б)
; б) 
 ; б)
; б)  1.26 а)
1.26 а)  ; б)
; б) 
 ; б)
; б)  1.28 а)
1.28 а) 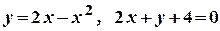 ; б)
; б) 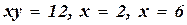
 ; б)
; б)  1.30 а)
1.30 а)  ; б)
; б) 
 ; б)
; б) 
 ; б)
; б) 
 ; б)
; б) 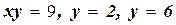
 ; б)
; б) 
 ; б)
; б)  ,
, 
 ; б)
; б) 
 ; б)
; б) 
 ; б)
; б) 
 ; б)
; б) 
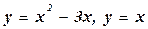 ; б)
; б) 
 ; б)
; б) 
 ; б)
; б) 
 ; б)
; б) 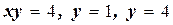
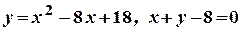 ; б)
; б)  ; б)
; б) 
 ; б)
; б) 
 ; б)
; б) 
 ; б)
; б) 

 ; б)
; б) 
 2.2 а)
2.2 а) 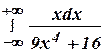 2.3 а)
2.3 а) 
 б)
б)  б)
б) 
 2.5 а)
2.5 а)  2.6 а)
2.6 а) 
 б)
б)  б)
б) 
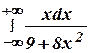 2.8 а)
2.8 а)  2.9 а)
2.9 а) 
 б)
б)  б)
б) 
 2.11 а)
2.11 а)  2.12 а)
2.12 а) 
 б)
б)  б)
б) 
 2.14 а)
2.14 а)  2.15 а)
2.15 а) 
 б)
б)  б)
б) 
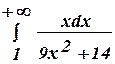 2.17 а)
2.17 а)  2.18 а)
2.18 а) 
 б)
б)  б)
б) 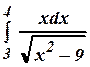
 2.20 а)
2.20 а)  2.21 а)
2.21 а) 
 б)
б)  б)
б) 
 2.23 а)
2.23 а) 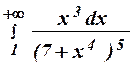 2.24 а)
2.24 а) 
 б)
б)  б)
б) 
 2.26 а)
2.26 а)  2.27 а)
2.27 а) 
 б)
б)  б)
б) 
 2.29 а)
2.29 а)  2.30. а)
2.30. а) 
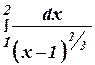 б)
б)  б)
б) 
 2.32 а)
2.32 а) 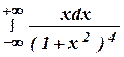 2.33 а)
2.33 а) 
 б)
б)  б)
б) 
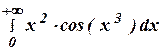 2.35 а)
2.35 а)  2.36 а)
2.36 а) 
 б)
б)  б)
б) 
 2.38 а)
2.38 а)  2.39 а)
2.39 а) 
 б)
б)  б)
б) 
 2.41 а)
2.41 а)  2.42 а)
2.42 а) 
 б)
б)  б)
б) 
 2.44 а)
2.44 а)  2.45 а)
2.45 а) 
 б)
б)  б)
б) 
 2.47 а)
2.47 а)  2.48 а)
2.48 а) 
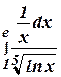 б)
б)  б)
б) 
 2.50 а)
2.50 а) 
 б)
б) 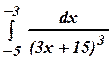

 3.2 а)
3.2 а) 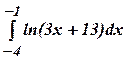 3.3 а)
3.3 а) 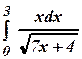
 б)
б) 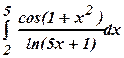 б)
б) 
 3.5 а)
3.5 а)  3.6 а)
3.6 а) 
 б)
б)  б)
б) 
 3.8 а)
3.8 а)  3.9 а)
3.9 а) 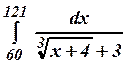
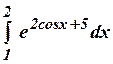 б)
б)  б)
б) 
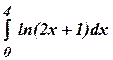 3.11 а)
3.11 а)  3.12 а)
3.12 а) 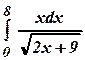
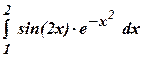 б)
б)  б)
б) 
 3.14 а)
3.14 а)  3.15 а)
3.15 а) 
 б)
б) 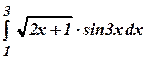 б)
б) 
 3.17 а)
3.17 а)  3.18 а)
3.18 а) 
 б)
б)  б)
б) 
 3.20 а)
3.20 а)  3.21 а)
3.21 а) 
 б)
б) 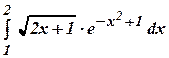 б)
б) 
 3.23 а)
3.23 а)  3.24 а)
3.24 а) 
 б)
б)  б)
б) 
 3.26 а)
3.26 а)  3.27 а)
3.27 а) 
 б)
б)  б)
б) 
 3.29 а)
3.29 а) 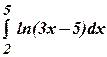 3.30 а)
3.30 а) 
 б)
б)  б)
б) 
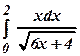 3.32 а)
3.32 а)  3.33 а)
3.33 а) 
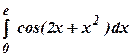 б)
б) 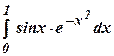 б)
б) 
 3.35 а)
3.35 а)  3.36 а)
3.36 а) 
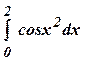 б)
б)  б)
б) 
 3.38 а)
3.38 а)  3.39 а)
3.39 а) 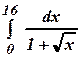
 б)
б)  б)
б) 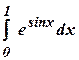
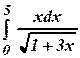 3.41 а)
3.41 а)  3.42 а)
3.42 а) 
 б)
б)  б)
б) 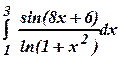
 3.44 а)
3.44 а)  3.45 а)
3.45 а) 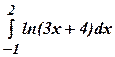
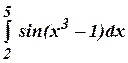 б)
б)  б)
б) 
 3.47 а)
3.47 а) 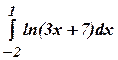 3.48 а)
3.48 а) 
 б)
б)  б)
б) 
 3.50 а)
3.50 а) 
 б)
б)