Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вычисление криволинейного интеграла первого рода.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Параметризуем дугу L: AB x = x(t), y = y(t), z =z (t). Пусть t0 соответствует точке A, а t1 соответствует точке B. Тогда криволинейный интеграл первого рода сводится к определенному интегралу (
Пример. Вычислить массу одного витка однородной (плотность равна k) винтовой линии:
Криволинейный интеграл 2 рода. Задача о работе силы.
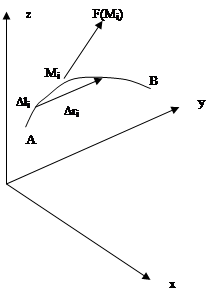
1. Организуем разбиение области- дуги AB на элементы – элементарные дуги 2. Отметим на элементах разбиения «отмеченные точки» Mi и вычислим в них значения функции 3. Построим интегральную сумму 4. Переходя к пределу при условии
Теорема существования. Пусть вектор - функция
Замечание. Предел этот не зависит от - способа выбора разбиения, лишь бы выполнялось условие А - выбора «отмеченных точек» на элементах разбиения, - способа измельчения разбиения, лишь бы выполнялось условие В
Свойства криволинейного интеграла 2 рода.
1. Линейность б) свойство однородности Доказательство. Запишем интегральные суммы для интегралов в левых частях равенств. Так как в интегральной сумме число слагаемых конечно, используя свойство скалярного произведения, перейдем к интегральным суммам для правых частей равенств. Затем перейдем к пределу, по теореме о предельном переходе в равенстве получим желаемый результат.
2. Аддитивность. Доказательство. Выберем разбиение области L так, чтобы ни один из элементов разбиения (первоначально и при измельчении разбиения) не содержал одновременно как элементы L1, так и элементы L2. Это можно сделать по теореме существования (замечание к теореме). Далее проводится доказательство через интегральные суммы, как в п.1. 3. Ориентируемость.
Доказательство. Интеграл по дуге –L, т..е. в отрицательном направлении обхода дуги есть предел интегральных сумм, в слагаемых которых вместо Заметим, что свойство ориентируемости в криволинейном интеграле первого рода отсутствует. Зато в криволинейном интеграле второго рода отсутствуют свойства интегрирования неравенств, теорема об оценке и теорема о среднем, которые есть в криволинейном интеграле первого рода.
Вычисление криволинейного интеграла второго рода. . Пусть Тогда криволинейный интеграл второго рода можно записать в виде
Параметризуем дугу L = AB:
Пример. Вычислить
Пример. Вычислить интеграл 1) 2) 3) Пример. Показать, что
Лекция 6. Формула Грина.
Теорема (формула) Грина. Пусть G – плоская односвязная область с кусочно-гладкой границей L. Пусть функции P(x, y), Q(x, y) непрерывны и имеют непрерывные частные производные по своим переменным в области G и на L. Тогда справедлива формула Грина
Доказательство. 1) Назовем плоскую область D (в плоскости OXY) правильной, если любая прямая, параллельная координатной оси (OX или OY) пересекает область не более, чем в двух точках. Можно показать, что область G можно представить как объединение конечного числа правильных областей Тогда по свойству аддитивности двойной интеграл в правой части формулы Грина равен сумме двойных интегралов по правильным областям. Криволинейный интеграл в левой части равен сумме криволинейных интегралов по границам правильных областей, так как криволинейные интегралы по общим границам любых правильных областей различны по знаку из-за различных направлений обхода границы и взаимно уничтожаются при суммировании. Поэтому доказательство может быть проведено для правильной области G. 2) Пусть G – правильная область. Так как P, Q могут быть произвольными функциями, то формула Грина сводится двум формулам
|
||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 660; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.33 (0.007 с.) |

 - известная из 1 семестра формула для вычисления дифференциала длины дуги):
- известная из 1 семестра формула для вычисления дифференциала длины дуги):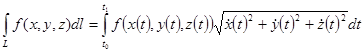
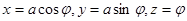 .
. .
.
 , где
, где 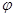 - угол между векторами. В общем случае эту формулу можно использовать для построения интегральной суммы, предполагая силу постоянной на элементе дуги
- угол между векторами. В общем случае эту формулу можно использовать для построения интегральной суммы, предполагая силу постоянной на элементе дуги  достаточно малой длины. Вместо длины малого элемента дуги можно взять длину стягивающей ее хорды
достаточно малой длины. Вместо длины малого элемента дуги можно взять длину стягивающей ее хорды  , так как эти величины – эквивалентные бесконечно малые величины при условии
, так как эти величины – эквивалентные бесконечно малые величины при условии 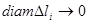 (первый семестр).
(первый семестр).
 (условие А)
(условие А)
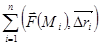 , где
, где 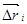 вектор, направленный по хорде, стягивающей -дугу
вектор, направленный по хорде, стягивающей -дугу  (условие В), получим криволинейный интеграл второго рода как предел интегральных сумм (и работу силы):
(условие В), получим криволинейный интеграл второго рода как предел интегральных сумм (и работу силы): . Часто обозначают
. Часто обозначают 
 непрерывна на кусочно-гладкой дуге L[12]. Тогда криволинейный интеграл второго рода существует как предел интегральных сумм.
непрерывна на кусочно-гладкой дуге L[12]. Тогда криволинейный интеграл второго рода существует как предел интегральных сумм. .
.
 .
. , то
, то  =
= 
 +
+  .
.
 стоит (
стоит ( ). Вынося «минус» из скалярного произведения и из суммы конечного числа слагаемых, переходя к пределу, получим требуемый результат.
). Вынося «минус» из скалярного произведения и из суммы конечного числа слагаемых, переходя к пределу, получим требуемый результат. .
. .
. ,
,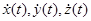 непрерывны, так как дуга гладкая. Подставим эти выражения в криволинейный интеграл, он превратится в определенный интеграл по параметру.
непрерывны, так как дуга гладкая. Подставим эти выражения в криволинейный интеграл, он превратится в определенный интеграл по параметру.
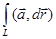 , где
, где  - один виток винтовой линии,
- один виток винтовой линии,  .
. .
. по трем различным дугам, соединяющим точки A(0,0,), B(1,1,)
по трем различным дугам, соединяющим точки A(0,0,), B(1,1,)  - ломаная, соединяющая точки A, C(1,0), B,
- ломаная, соединяющая точки A, C(1,0), B, 

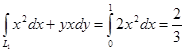 ,
,


 по всем указанным выше дугам.
по всем указанным выше дугам.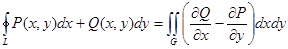 .
. .
. и
и  , каждую из которых надо доказать. Докажем первую формулу, вторая доказывается аналогично.
, каждую из которых надо доказать. Докажем первую формулу, вторая доказывается аналогично.
 =
= 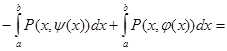 =
=  =
=
 =
=