Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Несобственный интеграл 1-го рода. Абсолютно сходящиеся интегралыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Определение Предположим, что функция
· Если эта функция имеет предел
а сам интеграл · Если наряду с собственным интегралом по бесконечному промежутку Если интеграл
2. Сходимость интегралов в случае положительных функций Если функция положительна (неотрицательна), то интеграл
представляет собой монотонно возрастающую функцию от переменной А. Для сходимости несобственного интеграла - в случае положительной функции - необходимо и достаточно, чтобы интеграл при возрастании А оставался ограниченным сверху.
3. Сходимость интеграла в общем случае. Признак Абеля. Признак сходимости Дирихле. Теорема 1 (признак Дирихле). Если на полуосиx > a:
сходится. Теорема 2 (признак Абеля). Если на полуосиx > a:
сходится;
4. Несобственные интегралы 2-го рода. Разрывы подынтегральной функции. Пусть функция f (x) определена на полуинтервале (a, b ], интегрируема по любому отрезку Определение: Пусть функция f (x) имеет разрыв в точке х = b, а остальных точках этого промежутка (а; b) она непрерывна. Если существует конечный предел
Аналогично определяется несобственный интеграл, когда функция f (x) имеет разрыв в точке х = а:
Определение: Пусть функция f (x) имеет разрыв в точке х = а, а остальных точках этого промежутка (а; b) она непрерывна. Если существует конечный предел
Определение 7: Пусть функция f (x) имеет разрыв во внутренней точке с промежутка (а; b), а остальных точках этого промежутка он
5 Условия и признаки существования интеграла · Признак сравнения в предельной форме. Пусть неотрицательные функции f (x) и g (x) интегрируемы по любому отрезку [ a, b ] и пусть существует конечный · Признак сравнения. Пусть функции f (x) и g (x) интегрируемы по любому отрезку [ a, b ] и при
6. Главное значение несобственного интеграла Пусть интеграл
и выполним предельный переход, устремив к нулю Если существует двойной предел выражения (1), не зависящий от способа предельного перехода, то он называется несобственным интегралом от функции f (x) по промежутку [ a, b ]:
В этом случае
где F (x) – первообразная функции f (x). Если предел (2) существует лишь при согласованном предельном переходе, а именно когда
В таких случаях говорят, что интеграл
7 Свойства несобственных интегралов Свойства несобственных интегралов второго рода, по сути дела, повторяют свойства несобственных интегралов первого рода: меняется лишь база предела, задающего несобственный интеграл, с
на
1. Пусть фиксированы числа
2. (теоpемасpавнения) Пусть даны две функции 3. Тогда из сходимости интеграла от большей функции следует сходимость интеграла от меньшей функции, причём
а из расходимости интеграла от меньшей функции, следует расходимость интеграла от большей функции:
.3 Если интеграл
причём имеет место неравенство
· Если несобственный интеграл · Если несобственный интеграл
8. Интегрирование по частям. Пусть u = u(x) и v = v(x) – функции, имеющие непрерывные производные. Тогда d(uv) = u*dv + v*duИнтегрирую это равенство получим формулу интегрирования по частям, она дает возможность свести вычисление интеграла
Интегрирование по частям состоит в том, что подынтегральное выражение заданного интеграла представляется каким-либо образом в виде произведения двух сомножителей u и dv (это, как правило, можно осуществить несколькими); затем, после нахождения v и du, используется формула интегрирования по частям. Иногда эту формулу приходиться использовать несколько раз.
9. Замена переменных в несобственных интегралов.
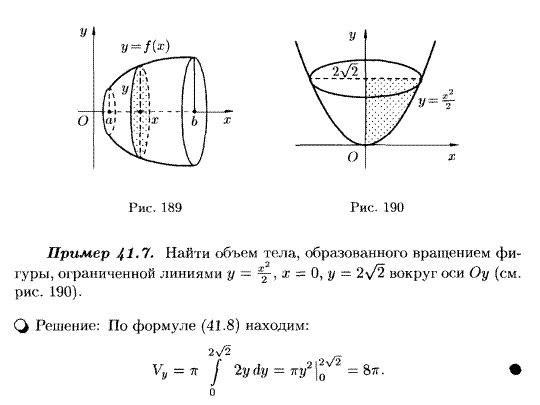
1. Вычисление площадей. Площадь, ограниченная одной кривой. Площадь, заключенная между двумя кривыми. Площадь сектора, ограниченного кривой, заданной в полярной системе координат.
2. Длина дуги кривой, заданной параметрически, заданной явно и заданной в полярных координатах.
3. Вычисление объемов тел вращения 4. Вычисление объёмов тел по их поперечным сечениям
5. Вычисление поверхности тел вращения.
6. Вычисление пути, пройденного телом.
7. Вычисление работы сил.
8. Вычисление статических моментов и центра тяжести материальной кривой. Первая теорема Гульдина.
9. Вычисление статических моментов и центра тяжести плоской фигуры. Вторая теорема Гульдина.
|
||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 1144; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.113.254 (0.01 с.) |

 задана на бесконечном промежутке вида
задана на бесконечном промежутке вида  и интегрируема на любом конечном отрезке
и интегрируема на любом конечном отрезке  , где
, где  . Таким образом, мы можем рассмотреть функцию
. Таким образом, мы можем рассмотреть функцию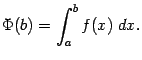
 то число
то число  называется значением несобственного интеграла первого рода
называется значением несобственного интеграла первого рода
 называется сходящимся (иными словами, интеграл
называется сходящимся (иными словами, интеграл  сходится и интеграл
сходится и интеграл  по этому же промежутку, то первый интеграл называется Абсолютно сходящимся.
по этому же промежутку, то первый интеграл называется Абсолютно сходящимся.
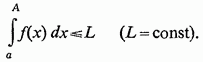
 +
+  , т. е.
, т. е. 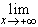 g (x) = 0; то интеграл
g (x) = 0; то интеграл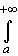 f (x) g (x) dx
f (x) g (x) dx
 , и имеет бесконечный предел при
, и имеет бесконечный предел при  . Несобственным интегралом от f (x) по отрезку [ a, b ] называется предел
. Несобственным интегралом от f (x) по отрезку [ a, b ] называется предел  . Если этот предел конечен, говорят, что интеграл сходится; если предел не существует или бесконечен, говорят, что интеграл расходится.
. Если этот предел конечен, говорят, что интеграл сходится; если предел не существует или бесконечен, говорят, что интеграл расходится. , то его называют несобственным интегралом второго рода и обозначают
, то его называют несобственным интегралом второго рода и обозначают 

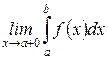 , то его называют несобственным интегралом второго рода и обозначают
, то его называют несобственным интегралом второго рода и обозначают 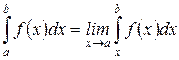

 . Тогда несобственные интегралы
. Тогда несобственные интегралы  и
и  сходятся или расходятся одновременно.
сходятся или расходятся одновременно. удовлетворяют неравенствам
удовлетворяют неравенствам  . Тогда:
. Тогда:  если сходится интеграл
если сходится интеграл  имеет единственную особенность во внутренней точке
имеет единственную особенность во внутренней точке  промежутка [ a, b ]. Составим сумму
промежутка [ a, b ]. Составим сумму
 и
и  .
.

 , то этот предел называется главным значением несобственного интеграла
, то этот предел называется главным значением несобственного интеграла  и обозначается символическим выражением
и обозначается символическим выражением
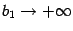 для интеграла
для интеграла
 для интеграла от функции с особенностью в точке
для интеграла от функции с особенностью в точке  :
: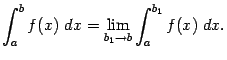
 и функция
и функция  , где
, где  , и имеет особенность в точке
, и имеет особенность в точке  сходится, то при любом
сходится, то при любом  сходится интеграл
сходится интеграл  . Обратно, если при некотором
. Обратно, если при некотором  , заданные на
, заданные на  и имеющие особенность в точке
и имеющие особенность в точке  выполняется неравенство
выполняется неравенство


 сходится, то сходится также интеграл
сходится, то сходится также интеграл 

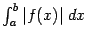 сходится, то несобственный интеграл
сходится, то несобственный интеграл  называется абсолютно сходящимся.
называется абсолютно сходящимся.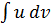 к вычислению интеграла
к вычислению интеграла  , который может оказаться существенно более простым, чем исходный.
, который может оказаться существенно более простым, чем исходный.