
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Производная и дифференциал сложной функцииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пусть функция y = f (x) задана в некоторой окрестности U = U (x 0) точки x 0, а функция z = g (y) - в некоторой окрестности V = V (y 0) точки y 0 = f (x 0), причем f (U) и, следовательно, определена сложная функция F (x) = g (f (x)). Теорема 5. Если функция y = f (x) имеет производную в точке x 0, а функция z = g (y) имеет производную в точке y 0 = f (x 0), то сложная функция z = F (x) = g (f (x)) также имеет в точке x 0 производную, причем
или, опуская значение аргумента,
Пусть, как всегда,
Поскольку функция y = f (x) непрерывна при x = x 0, то
Поделив обе части первого равенства (10.30) на
В силу равенств (10.31) и F' (x 0) = причем F' (x 0) = g' (y 0) f' (x 0). Следствие (инвариантность формы дифференциала).
или, короче, dz = z'xdx = z'ydy. Эта формула показывает, что формально записи дифференциала сложной функции посредством независимой переменной x и посредством зависимой переменной y имеют один и тот же вид, но следует иметь в виду, что здесь dx =
Пример. Вычислим производную функции y = xa, x > 0, a (xa) ' = (xa ln x) ' = (eu) 'uu'x = eua/x = ea ln xa/x = xaa/x = axa -1, т. е.
Производная и дифференциал неявно заданной функции Если независимая переменная Если функция описывается уравнением y = f (x), где переменная y находится в левой части, а правая часть зависит только от аргумента x, то говорят, что функция задана в явном виде.
для нахождения производной y' (x) неявно заданной функции нет необходимости преобразовывать ее в явную форму. Для этого, зная уравнение F (x, y) = 0, достаточно выполнить следующие действия: Сначала необходимо продифференцировать обе части уравнения по переменной x, предполагая, Замечание: Если правая часть отлична от нуля, т.е. неявное уравнение имеет вид
то дифференцируем левую и правую части уравнения.
Решить полученное уравнение относительно производной y' (x). Дифференцирование функций, заданных неявно Если функция задана уравнением у = f (x), разрешённым относительно y, то функция задана в явном виде (явная функция). Под неявным заданием функции понимают задание функции в виде уравнения F (х; у) = 0, не разрешённого относительно у. Всякую явно заданную функцию у = f (x) можно записать как неявно заданную уравнением f (x) - у = 0, но не наоборот. Не всегда легко, а иногда и невозможно разрешить уравнение относительно у (например, у + 2х + соs у - 1 = 0 или 2 y - х + у = 0). Если неявная функция задана уравнением F (х; у) = 0, то для нахождения производной от у по х нет необходимости разрешать уравнение относительно у: достаточно продиффиринцировать это уравнение по х, рассматривая при этом у как функцию от х и полученное затем уравнение разрешить относительно у′. Производная неявной функции выражается через аргумент х и функцию у. Пример. Найти производную функции у, заданную уравнением Решение: функция у задана неявно. Дифференцируем по х равенство полученного соотношения 3
|
|||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 745; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.189.192.214 (0.009 с.) |

 x = x - x 0,
x = x - x 0,  y = f' (x 0)
y = f' (x 0) 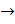 0,)
0,) z = g' (y 0)
z = g' (y 0)  (
( (
(
 (y) = z 0,) имеем
(y) = z 0,) имеем (
( 0, получим
0, получим y /
y /  (
( R, c помощью формулы (10.28). Для этого представим функцию y = xa как композицию функций y = eu и u = ln x. Заметив, что dy / du = eu, du / dx = a/x, получим
R, c помощью формулы (10.28). Для этого представим функцию y = xa как композицию функций y = eu и u = ln x. Заметив, что dy / du = eu, du / dx = a/x, получим и функция
и функция  связаны уравнением вида
связаны уравнением вида  , которое не разрешено относительно
, которое не разрешено относительно  - задана в явном виде.
- задана в явном виде. - задана неявным образом.
- задана неявным образом.

 . Из
. Из + 3⋅
+ 3⋅  ⋅у′ - 3 (1⋅у + х⋅у′) = 0 следует, что
⋅у′ - 3 (1⋅у + х⋅у′) = 0 следует, что  , т.е.
, т.е.



