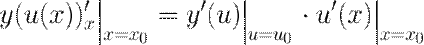Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифференциал функции. Теорема о дифференцируемости функции в точке. Теорема о связи дифференцируемости и непрерывности функции в точке.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Дифференциалом функции называется линейная относительно
Теорема Ферма. Пусть функция Теорема. Если функция Доказательство. Пусть функция
Существует и конечен. По определению предела это значит, что
То есть при малых Обратно, если функция
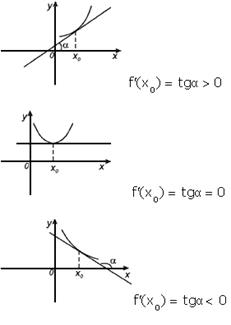
Геометрический смысл производной и дифференциала и физический смысл производной. Выясним геометрический смысл дифференциала. Для этого проведём к графику функции у = f (х) в точке М (х; у) касательную МТ и рассмотрим ординату этой касательной для точки х + Δх (рис. 2). На рисунке |АМ| = Δх, |А
Но, согласно геометрическому смыслу производной, tg α = f ′ (х). Поэтому АВ = f ′ (х)⋅Δх. Сравнивая полученный результат с формулой получаем dy = АВ, т.е. дифференциал функции у = f (х) в точке х равен приращению ординаты касательной к графику функции в этой точке, когда х получит приращение Δх.
Геометрический смысл производной заключается в том, что численно производная функции в данной точке равна тангенсу угла, образованного касательной, проведенной через эту точку к данной кривой, и положительным направлением оси Ох:
Геометрический смысл производной. Производная в точке x 0 равна угловому коэффициенту касательной к графику функции y = f (x) в этой точке.
Дифференцирование функций
Дифференциалом функции называется линейная относительно
Операция нахождения производной функции называется дифференцированием. Понятие дифференциала функции Дифференциалом функции у = f (х) в точке х называется главная часть её приращения, равная произведению производной функции на приращение аргумента, и обозначается dy (или df (x)): dy = f ′ (x)⋅Δx. Дифференциал dy называют также дифференциалом первого порядка. Найдём дифференциал независимой переменной х, т.е. дифференциал функции у = х. Так как у' = х' = 1, то имеем dy = dx = Δx, т.е. дифференциал независимой переменной равен приращению этой переменной: dx = Δx. Поэтому формулу можно записать так: dy = f ′ (x) dx, иными словами, дифференциал функции равен произведению производной этой функции на дифференциал независимой переменной.
Правила вычисления производных, связанные с арифметическими действиями над функциями. Производные алгебраической суммы, произведения, частного. Примеры Пусть функции и 1. Константу можно выносить за знак производной.
Пример: 2. Производная суммы/разности. Производная суммы/разности двух функций равна сумме/разности производных от каждой из функций.
Пример:
3. Производная произведения.
Пример:
4. Производная частного.
Пример:
5. Производная сложной функции. Производная сложной функции равна производной этой функции по промежуточному аргументу
|
|||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 648; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.59.242 (0.01 с.) |

 часть приращения функции. Она обозначается как
часть приращения функции. Она обозначается как 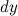 или
или 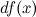 . Таким образом:
. Таким образом: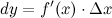
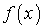 определена на интервале
определена на интервале 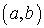 и в некоторой
и в некоторой имеет наибольшее или наименьшее значение. Тогда, если в
имеет наибольшее или наименьшее значение. Тогда, если в существует производная, то она равна нулю, то есть
существует производная, то она равна нулю, то есть 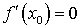 .
.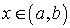 выполняется соотношение
выполняется соотношение 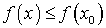 , а значит
, а значит 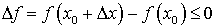 .Если
.Если 
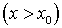 , то
, то 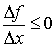 и
и 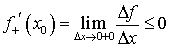 .Если
.Если 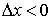
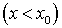 , то
, то  и
и 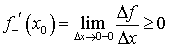 .Из существования производной следует, что
.Из существования производной следует, что 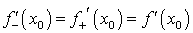 , а это возможно, только когда
, а это возможно, только когда  дифференцируема в точке X, то она и непрерывна в этой точке. Обратное не гарантировано.
дифференцируема в точке X, то она и непрерывна в этой точке. Обратное не гарантировано. существует и конечна в точке X. То есть
существует и конечна в точке X. То есть
 при
при 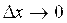 .
.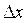 имеем
имеем 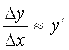 , откуда
, откуда 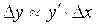 , причем это приближенное равенство тем точнее, чем меньше
, причем это приближенное равенство тем точнее, чем меньше  . А этои означает непрерывность функции
. А этои означает непрерывность функции 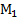 | = Δу. Из прямоугольного треугольника МАВ имеем:
| = Δу. Из прямоугольного треугольника МАВ имеем: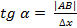 , т.е.
, т.е. 


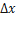 часть приращения функции. Она обозначается как
часть приращения функции. Она обозначается как 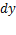 или
или 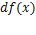 . Таким образом:
. Таким образом: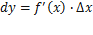
 и
и 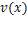 имеют производные в точке x. Тогда
имеют производные в точке x. Тогда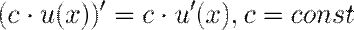


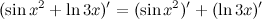
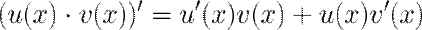
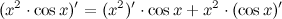
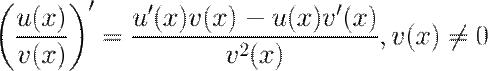
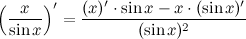
 , умноженной на производную от промежуточного аргумента
, умноженной на производную от промежуточного аргумента  .
.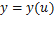 и
и 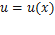 имеют производные соответственно в точках
имеют производные соответственно в точках  и
и 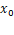 . Тогда
. Тогда