Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Раскрытие неопределенности. Правило ЛопиталяСодержание книги
Поиск на нашем сайте
Формула Тейлора. Теорема Тейлора. Ряд Маклорена Формула Тейлора показывает поведение функции в окрестности некоторой точки. Формула Тейлора функции часто используется при доказательстве теорем в дифференциальном исчислении.
Формула Тейлора
, где Rn(x) - остаточный член формулы Тейлора.
Остаточный член формулы Тейлора
В форме Лагранжа:
В форме Коши:
Формулировка теоремы Точная формулировка большинства базовых версий теоремы такова. Теорема Тейлора [1] Пусть k ≥ 1 является целым, и пусть функция f: R → R является k раз дифференцируемой в точке a ∈ R. Тогда существует функция hk: R → R такая, что
Многочлен, возникающий в теореме Тейлора, является многочленом Тейлора k -го порядка
функции f в точке a. Теорема Тейлора описывает асимптотическое поведение остаточного члена
который является ошибкой при нахождении приближения функции f с помощью многочленов Тейлора. Используя «O» большое и «o» малое теорему Тейлора можно сформулировать так
Если функция f (x) имеет непрерывные производные вплоть до (n+ 1)-го порядка, то ее можно разложить в степенной ряд по формуле Тейлора:
где Rn − остаточный член в форме Лагранжа определяется выражением
Если приведенное разложение сходится в некотором интервале x, т.е. Если a = 0, то такое разложение называется рядом Маклорена:
Разложение некоторых функций в ряд Маклорена · · · · · 46. ряды Маклорена для элементарных функций Исследование функций. Условие постоянства функции. Признак монотонности функции Исследование функции и построение ее графика При построении графика функции необходимо провести ее предварительное исследование. Примерная схема исследования функции с целью построения ее графика имеет следующую структуру: 1. Область определения 2. Четность, нечетность функции. 3. Точки пересечения с осями. 4. Асимптоты функции. 5. Экстремумы и интервалы монотонности. 6. Точки перегиба и промежутки выпуклости, вогнутости. 7. Сводная таблица. Постоянство ф-ции. Теорема. Пусть Доказательство. Необходимость. Пусть Достаточность. Пусть
т.е.
|
||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 475; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.72.200 (0.01 с.) |

 Пусть заданы две функции f (x) и g (x), такие, что
Пусть заданы две функции f (x) и g (x), такие, что
 В этом случае говорят, что функция
В этом случае говорят, что функция 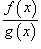 имеет неопределенность типа
имеет неопределенность типа  Пусть две функции f (x) и g (x) обладают свойством
Пусть две функции f (x) и g (x) обладают свойством
 где a является действительным числом, либо стремится к + ∞ или − ∞. Говорят, что в этом случае функция
где a является действительным числом, либо стремится к + ∞ или − ∞. Говорят, что в этом случае функция  Неопределенности этих типов сводятся к рассмотренным выше неопределенностям типа
Неопределенности этих типов сводятся к рассмотренным выше неопределенностям типа  . Пусть a является некоторым конечным действительным числом или равно бесконечности.
· Если
. Пусть a является некоторым конечным действительным числом или равно бесконечности.
· Если 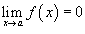 и
и  , то
, то  ;
· Если
;
· Если  и
и  , то аналогично
, то аналогично  . Первые две неопределенности
. Первые две неопределенности  можно свести к типу
можно свести к типу  сводятся к типу
сводятся к типу  с помощью соотношения
с помощью соотношения





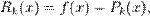



 , то оно называется рядом Тейлора, представляющим разложение функции f (x) в точке a.
, то оно называется рядом Тейлора, представляющим разложение функции f (x) в точке a.






 и область допустимых значений
и область допустимых значений  функции.
функции. определена и непрерывна на промежутке
определена и непрерывна на промежутке  Для того, чтобы она была равна константе необходимо и достаточно, чтобы
Для того, чтобы она была равна константе необходимо и достаточно, чтобы 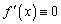 .
. . Но тогда
. Но тогда  .
.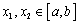 . Тогда по формуле Лагранжа
. Тогда по формуле Лагранжа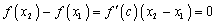
 . Так как это верно для любых
. Так как это верно для любых  и
и  то отсюда следует, что
то отсюда следует, что