Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Комплексные числа. Сложение и вычитание, умножение и деление кч. Возведение в степень и извлечение корня.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Комплексные числа записываются в виде: a+ bi. Здесь a и b – действительные числа, а i – мнимая единица, т.e. i 2 = –1.Число a называется абсциссой, a b – ординатой комплексного числа a+ bi. Два комплексных числа a+ bi и a – bi называются сопряжёнными комплексными числами. Сложение. Суммой комплексных чисел a+ bi и c+ di называется комплексное число (a+ c) + (b+ d) i. Таким образом, при сложениикомплексных чисел отдельно складываются их абсциссы и ординаты. Это определение соответствует правилам действий с обычными многочленами.
Вычитание. Разностью двух комплексных чисел a+ bi (уменьшаемое) и c+ di (вычитаемое) называется комплексное число (a – c) + (b – d) i. Таким образом, при вычитании двух комплексных чисел отдельно вычитаются их абсциссы и ординаты.
Умножение. Произведением комплексных чисел a+ bi и c+ di называется комплексное число: (ac – bd) + (ad + bc) i. Это определение вытекает из двух требований:
1) числа a+ bi и c+ di должны перемножаться, как алгебраические двучлены, 2) число i обладает основным свойством: i 2 = – 1. Деление. Разделить комплексное число a+ bi (делимое) на другое c+ di (делитель) - значит найти третье число e+ f i (чатное), которое будучи умноженным на делитель c+ di, даёт в результате делимое a+ bi. Если делитель не равен нулю, деление всегда возможно. Возведение в степень:
где n – целое положительное число. (Отметим, что перемножать, делить и возводить в степень часто удобнее, когда комплексное число задается в тригонометрической или показательной форме) Извлечение корня из комплексного числа Определение Корнем
Корень Если комплексное число
Геометрически все значения корня лежат на окружности радиуса Показательная функция. Формулы Эйлера. Логарифм комплексного числа Показательная функция Функцию вида y=ax, где а>0, a≠1, х – любое число, называют показательной функцией.
· Область определения показательной функции: D (y)= R – множество всех действительных чисел. · Область значений показательной функции: E (y)= R+ - множество всех положительных чисел. · Показательная функция y=ax возрастает при a>1. · Показательная функция y=ax убывает при 0<a<1. Справедливы все свойства степенной функции: · а0=1 Любое число (кроме нуля) в нулевой степени равно единице. · а1=а Любое число в первой степени равно самому себе. · ax∙ay=ax+y При умножении степеней с одинаковыми основаниями основание оставляют прежним, а показатели складывают. · ax:ay=ax- y При делении степеней с одинаковыми основаниями основание оставляют прежним, а из показателя степени делимого вычитают показатель степени делителя. · (ax)y=axy При возведении степени в степень основание оставляют прежним, а показатели перемножают · (a∙b)x=ax∙by При возведении произведения в степень возводят в эту степень каждый из множителей. · (a/b)x=ax/by При возведении дроби в степень возводят в эту степень и числитель и знаменатель дроби. · а-х=1/ax · (a/b)-x=(b/a)x. · Формула Эйлера
Логарифм комплексного числа
|
|
| Поделиться: |

 ,
,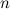 -ой степени из комплексного числа
-ой степени из комплексного числа  называется такое комплексное число
называется такое комплексное число 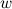 ,
, 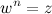
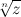 и на множестве комплексных чисел имеет ровно
и на множестве комплексных чисел имеет ровно 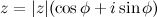 , то все значения корня
, то все значения корня 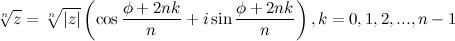
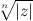 с центром в начале координат и образуют правильный
с центром в начале координат и образуют правильный 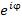 и тригонометрическими функциями
и тригонометрическими функциями 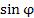 и
и 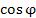 на множестве комплексных чисел:
на множестве комплексных чисел: .
.
 Заметим, что
Заметим, что 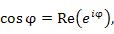 .
. 
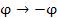 :
:
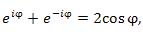
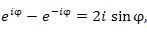
 .
. 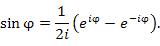
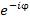 .
. 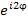 :
: