
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Разложение полинома на множители. Кратные корни. Теорема о необходимом и достаточном условии существовании кратного корняСодержание книги
Поиск на нашем сайте
Любой многочлен степени n вида Эта теорема сформулирована для комплексных корней Если коэффициенты К примеру, если корни Замечание. Среди корней многочлена могут быть повторяющиеся. Доказательство теоремы проводится с использованием основной теоремы алгебры и следствия из теоремы Безу.
Определение. Число В силу теоремы Безу это равносильно тому, что Определение. Число Теорема. Если Доказательство. Пусть
1. Если 2. Если Наибольший общий делитель. Алгоритм Евклида Общим делителем нескольких чисел называется число, которое является делите-лем каждого из них. Например, числа 36, 60, 42 имеют общие делители 2, 3 и 6. Среди всех общих делителей всегда есть наибольший, в данном случае это 6. Это и есть наибольший общий делитель (НОД). Чтобы найти наибольший общий делитель (НОД) нескольких чисел надо: 1) представить каждое число как произведение его простых множителей, например: 360 = 2 · 2 · 2 · 3 · 3 · 5, 2) записать степени всех простых множителей: 360 = 2 · 2 · 2 · 3 · 3 · 5 = 23 · 32 · 51, 3) выписать все общие делители (множители) этих чисел; 4) выбрать наименьшую степень каждого из них, встретившуюся во всех произведениях; 5) перемножить эти степени. Алгоритм Евклида для целых чисел Пусть
определена тем, что каждое
Тогда НОД(a, b), наибольший общий делитель Существование таких Корректность этого алгоритма вытекает из следующих двух утверждений: Пусть Операция освобождения полинома от кратных корней
Вещественные полиномы. Разложение полинома на множители первой и второй степени.
Выражения вида Как известно, если комплексное число
представляет собой квадратичное выражение. Таким образом, любой многочлен с действительными коэффициентами всегда можно представить в виде произведения линейных и квадратичных множителей
где Подбор корней многочлена. В общем случае найти корни многочлена степени n довольно сложная задача, но можно попытаться найти хотя бы один корень x0. Разделив исходный многочлен на одночлен x-x0, мы получим многочлен степени n-1. Тем самым мы упростили исходную задачу, так как раскладывать на множители теперь надо многочлен степени n-1. Например, для многочлена третьей степени после деления на x0 мы получим многочлен второй степени, корни которого найдем, просто решив квадратное уравнение. Существенную помощь в подборе рациональных корней многочлена может оказать следующая теорема. Теорема. Если многочлен a(x)= an*xn + an-1*xn-1 + an-2*xn-2 +... + a1*x + a0, an ≠ 0 c целыми коэффициентами имеет рациональный корень x0 = p/q (причем эта дробь несократима), то p – делитель свободного члена a0, а q – делитель старшего коэффициента an. Из этой теоремы следует, что если старший коэффициент равен единице, то целые корни многочлена следует искать только среди делителей свободного члена.
|
||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 2145; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.008 с.) |

 представляется произведением постоянного множителя при старшей степени
представляется произведением постоянного множителя при старшей степени  и n линейных множителей
и n линейных множителей  , i=1, 2, …, n, то есть
, i=1, 2, …, n, то есть  , причем
, причем  , i=1, 2, …, n являются корнями многочлена.
, i=1, 2, …, n являются корнями многочлена. , k=0, 1, 2, …, n. Она является основой для разложения любого многочлена на множители.
, k=0, 1, 2, …, n. Она является основой для разложения любого многочлена на множители.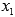 и
и  многочлена
многочлена  , где
, где 
 называется корнем полинома
называется корнем полинома  , если
, если  .
. .
. полинома
полинома  и
и  . Корни кратности 1 называются простыми корнями, корни кратности больше 1 называются кратными корнями.
. Корни кратности 1 называются простыми корнями, корни кратности больше 1 называются кратными корнями. полинома
полинома  . Если
. Если  , то
, то 

 , то
, то  и
и  — целые числа, не равные одновременно нулю, и последовательность чисел
— целые числа, не равные одновременно нулю, и последовательность чисел
 — это остаток от деления предпредыдущего числа на предыдущее, а предпоследнее делится на последнее нацело, то есть
— это остаток от деления предпредыдущего числа на предыдущее, а предпоследнее делится на последнее нацело, то есть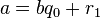






 , последнему ненулевому члену этой последовательности.
, последнему ненулевому члену этой последовательности. , то есть возможность деления с остатком
, то есть возможность деления с остатком  на
на 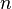 для любого целого
для любого целого 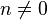 , доказывается индукцией по m.
, доказывается индукцией по m. , тогда НОД (a, b) = НОД (b, r).
, тогда НОД (a, b) = НОД (b, r).



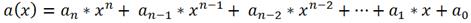 называются многочленами от x степени n (an ≠ 0) с действительными коэффициентами, если ai, i = 0,1,2,..., n - действительные числа.
называются многочленами от x степени n (an ≠ 0) с действительными коэффициентами, если ai, i = 0,1,2,..., n - действительные числа. – корень многочлена, то обязательно и комплексно сопряженное ему число
– корень многочлена, то обязательно и комплексно сопряженное ему число  является корнем многочлена. Поэтому их произведение
является корнем многочлена. Поэтому их произведение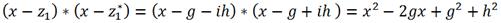

 , а x1,..., xs - действительные корни многочлена. То есть, если известны все корни многочлена с действительными коэффициентами, то можно сразу написать его разложение на множители.
, а x1,..., xs - действительные корни многочлена. То есть, если известны все корни многочлена с действительными коэффициентами, то можно сразу написать его разложение на множители.


