
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные свойства б.м. и б.б. последовательностейСодержание книги
Поиск на нашем сайте
1° Сумма б.м. последовательностей есть б.м.п. 2° Произведение ограниченной последовательности и б.м. есть б.м.п. 3° Если 4° Произведение б.м.п. есть последовательность б.м. 5° Если 6° Если 7° Если
Билет 10 Неопределенные выражения Неопределенные выражения (неопределенности). Иногда при формальной подстановке числа а вместо аргумента х под знак функции у = f (x) и дальнейшем проведении алгебраических действий над получившимся выражением или при переходе к пределу получаются выражения типа: Эти выражения бессмысленны с алгебраической точки зрения. Иногда, исходя из понятий математического анализа, таким выражениям удается придать определенный удобный смысл. Чаще всего, в случае непрерывности функции у = f (x) в некоторой окрестности точки х = а, исключая саму эту точку, под f (a) понимают Более того, неопределенные выражения часто возникают при вычислении пределов функций, построении графиков и т.д. В этих случаях имеется ряд приемов «раскрытия неопределенностей». Иногда неопределенными называют выражения, предел которых не может быть найден путем непосредственного применения теорем о пределе. Основными инструментами для раскрытия неопределённостей служат: формула Тейлора,первый замечательный предел, второй замечательный предел, правило Лопиталя и т.п.
Билет 11 Определение последовательности. ТеоремаБольцано-Вейерштрасса Последовательностью называется функция, которая переводит множество натуральных чисел Элемент Обычно последовательность целесообразнее задавать формулой ее общего члена, которая позволяет найти любой член последовательности, зная его номер. Другим способом задания последовательности является задание последовательности с помощью рекуррентного соотношения. В этом случае задается один или несколько первых элементов последовательности, а остальные определяются по некоторому правилу. Например, известен первый член
Теорема Больцано-Вейерштрасса (или лемма Больцано-Вейерштрасса о предельной точке). Из всякой ограниченной последовательности точек пространства Так как последовательность ограничена, то она имеет хотя бы одну предельную точку Из любой ограниченной последовательности можно выделить монотонную подпоследовательность. Действительно, согласно теореме Больцано-Вейерштрасса, из любой ограниченной последовательности можно выделить сходящуюся подпоследовательность, а из этой подпоследовательности можно выделить монотонную подпоследовательность. Пусть
Билет 12 Критерий Коши сходимости последовательностей В математике сходимость означает существование конечного предела у числовой последовательности или суммы бесконечного ряда или несобственного интеграла. Соответственно, расходимость — отсутствие конечного предела. Из определения сходимости последовательности Определение. Подпоследовательность Последовательность
Теорема (Критерий Коши). Для того, чтобы последовательность
Билет 13 Число е e — основание натурального логарифма, математическая константа, иррациональное и трансцендентное число. Иногда число e называют числом Эйлера или числом Непера. Обозначается строчной латинской буквой «e».
Максимум функции Число e играет важную роль в дифференциальном и интегральном исчислении, а также во многих других разделах математики. Поскольку функция экспоненты Число e может быть определено несколькими способами.
Билет 14 Предел функции. Определение окрестности предела. Определение предела по Гейне на языке последовательностей. Определение предела по Коши. Теорема о равносильности определений по Гейне и по Коши Преде́лфу́нкции (предельное значение функции) в заданной точке, предельной для области определения функции, — такая величина, к которой стремится значение рассматриваемой функции при стремлении её аргумента к данной точке. Предел функции является обобщением понятия предела последовательности: изначально под пределом функции в точке понимали предел последовательности элементов области значений функции, составленной из образов точек последовательности элементов области определения функции, сходящейся к заданной точке (предел в которой рассматривается); если такой предел существует, то говорят, что функция сходится к указанному значению; если такого предела не существует, то говорят, что функция расходится. Наиболее часто определение предела функции формулируют на языке окрестностей. То, что предел функции рассматривается только в точках, предельных для области определения функции, означает, что в каждой окрестности данной точки есть точки области определения; это позволяет говорить о стремлении аргумента функции (к данной точке). Но предельная точка области определения не обязана принадлежать самой области определения: например, можно рассматривать предел функции на концах открытого интервала, на котором определена функция (сами концы интервала в область определения не входят). Определение по Гейне (на языке последовательностей): Значение Определение по Коши: Значение
Все данные выше определения предела функции в точке эквивалентны. Иными словами, из любого из них можно вывести любое другое, то есть выполнение одного из них неизбежно влечёт выполнение всех остальных. Билет 15 Односторонние пределы. Теорема о существовании предела Односторонний предел — предел числовой функции, подразумевающий «приближение» к предельной точке с одной стороны. Такие пределы называют соответственно левым и правым пределами. Число Число
Левый и правый пределы функции называются односторонними пределами. Если существуют В случае, если
Признаки существования пределов: (О пределе промежуточной функции). Если имеет место соотношение (О пределе монотонной функции). Если функция Ограниченная монотонная последовательность имеет предел.
Билет 16 Критерий Коши о существовании предела
Для того чтобы функция f, x
| f (x) - a | < Поэтому если x' | f (x") - f (x')| = |[ f (x") - a ] + [ a - f (x')]| < Докажем достаточность условий (6.39) для существования конечного предела Замечание. Сформулируем критерий Коши существования конечного предела функции в терминах неравенств для случая, когда x 0 - действительное число: функция f, x
|
||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 814; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.75.247 (0.008 с.) |

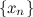 -б.м.п., то
-б.м.п., то  , то
, то 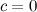 , т.е.
, т.е. 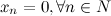
 , то последовательность
, то последовательность  - б.б.п.
- б.б.п.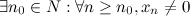 и последовательность
и последовательность 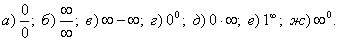 (*)
(*) .
. в некоторое множество
в некоторое множество 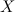 :
: 
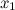 называется первым членом последовательности,
называется первым членом последовательности, 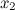 - вторым,...,
- вторым,...,  -
- 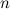 -ым или общим членом последовательности.
-ым или общим членом последовательности.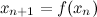 , то есть
, то есть 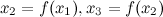 и так далее до нужного члена.
и так далее до нужного члена. можно выделить сходящуюся подпоследовательность.
можно выделить сходящуюся подпоследовательность. . В таком случае из этой последовательности можно выделить подпоследовательность, сходящуюся к точке
. В таком случае из этой последовательности можно выделить подпоследовательность, сходящуюся к точке  . Тогда предел
. Тогда предел  любой сходящейся подпоследовательности
любой сходящейся подпоследовательности  этой последовательности также находится на сегменте
этой последовательности также находится на сегменте  к точке a вытекает, что для любого
к точке a вытекает, что для любого  интервалом длиной 2
интервалом длиной 2  можно накрыть всю эту последовательность, исключением может быть конечное число ее элементов, если середину интервала поместить в точке
можно накрыть всю эту последовательность, исключением может быть конечное число ее элементов, если середину интервала поместить в точке  . Справедливо и обратное: если последовательность
. Справедливо и обратное: если последовательность  называется последовательностью Коши или фундаментальной, если
называется последовательностью Коши или фундаментальной, если 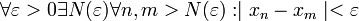
 существует номер
существует номер  такой, что для любых
такой, что для любых  выполняется неравенство:
выполняется неравенство: 
 -окрестности точки
-окрестности точки  содержатся все члены последовательности, начиная с этого номера.
содержатся все члены последовательности, начиная с этого номера.
 достигается при
достигается при  .
. интегрируется и дифференцируется «в саму себя», логарифмы именно по основанию e принимаются как натуральные.
интегрируется и дифференцируется «в саму себя», логарифмы именно по основанию e принимаются как натуральные. (второй замечательный предел).
(второй замечательный предел). или
или  .
.



 является функция
является функция  , где c — произвольная константа.
, где c — произвольная константа.


 называется пределом (предельным значением) функции
называется пределом (предельным значением) функции  в точке
в точке  , если для любой последовательности точек
, если для любой последовательности точек  , сходящейся к
, сходящейся к  сходится к
сходится к 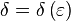 такое, что для всех аргументов
такое, что для всех аргументов 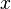 , удовлетворяющих условию
, удовлетворяющих условию  , выполняется неравенство
, выполняется неравенство  .
.
 называется правым пределом функции
называется правым пределом функции  в точке
в точке  , если для
, если для  такое, что для любого
такое, что для любого 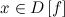 и
и  , выполняется неравенство
, выполняется неравенство  (рис. 1). Правый предел обозначается
(рис. 1). Правый предел обозначается 
 , выполняется неравенство
, выполняется неравенство 

 и
и  , причем
, причем  , то существует и
, то существует и  . Обратное утверждение также верно.
. Обратное утверждение также верно. , то предел
, то предел  не существует.
не существует. и
и  , то и
, то и 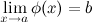
 или
или  , то соответственно существует ее левый предел
, то соответственно существует ее левый предел  X, имела в (конечной или бесконечно удаленной) точке x 0 конечный предел, необходимо и достаточно, чтобы для любого
X, имела в (конечной или бесконечно удаленной) точке x 0 конечный предел, необходимо и достаточно, чтобы для любого  > 0 существовала такая окрестность U (x 0) точки x 0, что для любых x'
> 0 существовала такая окрестность U (x 0) точки x 0, что для любых x'  U (x 0) и x"
U (x 0) и x"  Докажем необходимость условия (6.39). Пусть
Докажем необходимость условия (6.39). Пусть  f (x) = a
f (x) = a  x 0, xn
x 0, xn 
 > 0, что для всех точек
> 0, что для всех точек 


