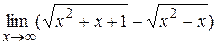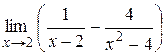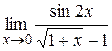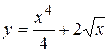Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 8. Неопределенный и определенный интегралыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Занятие 1 1. Повторение определений основных понятий темы. 2. Найти неопределенные интегралы методом непосредственного интегрирования а) Решить задачи [Л1, с.548 – 549]: 10.34 на дом 10.25; 10.32, 10.36. 3. Найти неопределенные интегралы методом замены переменной а) Решить задачи [Л1, с. 549, 554 – 556]: 10.41(в); 10.48 на дом 10.43; 10.46; 10.55; 10.76; 10.80; 10.90. 4. Найти неопределенные интегралы методом интегрирования по частям. Решить задачи [Л1, с. 556, 560]: 10.95(а); 10.97; 10.100; 10.104 на дом 10.107; 10.118, 10.125, 10.126. Занятие 2 1. Повторение определений основных понятий темы. 2. Найти неопределенные интегралы от рациональных дробей Решить задачи [Л1, с.565]: 10.127; 10.128; на дом 10.137; 10.140, 10.144, 10.150. 3. Вычислить определенные интегралы Решить задачи [Л1, с.621]: 11.32, 11.37, 11.50 на дом 11.40, 11.43 4. Найти площади фигур, ограниченных следующими кривыми а) Решить задачи [Л1, с.630]: 11.65 на дом 11.64; 11.72; 11.73; 11.84. 5. Вычислить несобственные интегралы а) Решить задачи [Л1, с.635 - 636]: 11.115; 11.118; 11.123 на дом 11.124; 11.128; 11.129; 11.133. ПЕРЕЧЕНЬ РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
1. Высшая математика для экономических специальностей. Учебник и Практикум (части I и II) / Под ред. Н.Ш. Кремера. М.: Высшее образование, 2008. 2. Учебно-методическое пособие по математике. Математическая логика. Дискретная математика. Линейная алгебра / Под ред. А.Н. Данчула. М.: Изд-во РАГС, 2004. 3. Грес П.В. Математика для гуманитариев. М.: Юрайт, 2000. 4. Эдельман С.Л. Математическая логика. М.: Высшая школа, 1975. 5. Гельман В.Я. Решение математических задач средствами Excel: Практикум/.– СПб.: Питер, 2003. 6. Сборник задач по математике. /А.Н.Данчул (отв.ред) / М.: Изд-во РАГС, 2005.
КОНТРОЛЬНЫЕ ЗАДАНИЯ Выполняются два контрольных задания по 6 задач в каждом. По выданному преподавателем номеру варианта задания с помощью таблицы вариантов, приведенной на следующей странице, определяются номера варианты входящих в задание задач. Образец оформления титульного листа задания приведен в Приложении. Сроки сдачи заданий: · задание 1 – 10 неделя (до 8 ноября); · задание 2 – 16 неделя (до 20 декабря). Сроки зачета заданий (с учетом исправления ошибок): · задание 1 – 11 неделя (до 15 ноября); · задание 2 – 17 неделя (до 27 декабря). Таблица вариантов
Контрольное задание №1
Задача 1. Даны матрицы A и B. Найти матрицу Вариант 1 Вариант 2
Вариант 3 Вариант 4
Вариант 5 Вариант 6
Вариант 7 Вариант 8
Вариант 9 Вариант 10
Задача 2. Найти матрицу, обратную матрице
Задача 4. Найти определитель произведения двух матриц Вариант 1 Вариант 2 Вариант 3 Вариант 4 Вариант 5 Вариант 6 Вариант 7 Вариант 8 Вариант 9 Вариант 10 Задача 4. Найти ранг матрицы
Задача 5. Записать систему уравнений в матричном виде и решить ее как матричное уравнение. Вариант 1 Вариант 2 Вариант 3
Вариант 4 Вариант 5 Вариант 6
Вариант 7 Вариант 8 Вариант 9
Вариант 10
Задача 6. Решить систему уравнений методом Гаусса Вариант 1 Вариант 2 Вариант 3
Вариант 4 Вариант 5 Вариант 6
Вариант 7 Вариант 8 Вариант 9
Вариант 10
Контрольное задание №2
Задача 1. Представить вектор x в виде линейной комбинации векторов a1, a2, a3, если система векторов a1, a2, a3 линейно независима. В случае линейной зависимости векторов a1, a2, a3 заменить один из них на вектор x так, чтобы полученная система стала линейно независимой.
Вариант 1 Вариант 2
Вариант 3 Вариант 4
Вариант 5 Вариант 6
Вариант 7 Вариант 8
Вариант 9 Вариант 10
Задача 2. Найти матрицу линейного преобразования, переводящего каждый вектор x двухмерного линейного пространства в вектор y по следующему алгоритму:
Задача 3. Даны вершины треугольника
Задача 4. Вычислить пределы функций
Задача 5. Исследовать функцию и построить график.
Задача 6. Найти неопределенный интеграл.
ВОПРОСЫ К ЭКЗАМЕНУ 1. Матрицы и основные операции над ними. 2. Виды матриц. Геометрическая интерпретация векторов. 3. Умножение матриц. 4. Определители матриц второго и третьего порядка. 5. Обратная матрица и ее нахождение. 6. Свойства определителей. 7. Элементарные преобразования строк и столбцов матрицы. Их использование при нахождении определителей. 8. Ранг матрицы. Способы вычисления ранга матрицы. 9. Теорема Кронекера-Капелли совместимости системы линейных алгебраических уравнений. 10. Запись и решение системы линейных алгебраических уравнений в матричном виде. 11. Решение системы линейных алгебраических уравнений методом Гаусса.
12. Вычисление обратной матрицы методом Гаусса. 13. Общее решение системы линейных алгебраических уравнений; свободные неизвестные, базисные решения. 14. Линейное пространство. 15. Линейная зависимость и независимость векторов. Способы определения. 16. Базис линейного пространства. Размерность линейного пространства 17.. Преобразование координат при переходе к новому базису. 18. Скалярное произведение векторов. Угол между векторами 19.. Ортонормированный базис. Евклидово пространство 20. Линейные преобразования. Свойства. 21. Нахождение матрицы линейного преобразования. 22..Определение, геометрическая интерпретация и формы записи комплексных чисел. 23. Операции над комплексными числами. 24. Собственные значения и собственные векторы матриц, свойства собственных векторов. 25. Уравнения прямой в двухмерном пространстве 26. Условия параллельности и перпендикулярности 27. Уравнения прямой в трехмерном пространстве 28. Уравнения плоскости в трехмерном пространстве 29. Понятие действительной функции действительной переменной. Способы задания функции. График функции. 30. Основные элементарные функции. Сложная и взаимно обратные функции. 31. Основные свойства функций. 32. Понятие числовой последовательности и основные свойства сходящихся последовательностей. 33. Предел числовой последовательности. Признаки существования предела последовательности. Два замечательных предела. 34. Предел функции в бесконечности и в точке. 35. Непрерывность функции действительной переменной в точке и на отрезке. 36. Свойства функций, непрерывных на отрезке. 37. Производная функции и дифференциал. 38. Производные и дифференциалы высших порядков. 39. Геометрический и физический смысл производной; геометрический смысл дифференциала. 40. Правила дифференцирования сумм, произведения и частного функций. Производная сложной и обратной функций. 41. Теоремы Ферма, Ролля, Лагранжа. 42. Правило Лопиталя. 43. Точки экстремума. Необходимое и достаточное условие локального экстремума функции. 44. Выпуклость и точки перегиба функции. Необходимое и достаточное условие перегиба функции. 45. Нахождение асимптот функции. 46. Уравнения касательной и нормали к графику функции в заданной точке. 47. Первообразная функции и неопределенный интеграл. 48. Свойства неопределенного интеграла. 49. Интегрирование рациональных дробей. 50. Понятие определенного интеграла. Свойства определенного интеграла.
51. Формула Ньютона-Лейбница. 52. Несобственные интегралы с бесконечными пределами. Признаки сходимости несобственных интегралов. 53. Несобственные интегралы от неограниченных функций. Признаки сходимости несобственных интегралов. 54. Геометрические приложения определенного интеграла.. ПРИЛОЖЕНИЕ.
Российская академия государственной службы при Президенте РФ
Задание N 1 по математике
Слушателя группы О-811 Иванова Петра Фомича Вариант 15
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 422; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.85.61 (0.011 с.) |

 ; б)
; б)  ; в)
; в)  .
. ; б)
; б)  ; в)
; в)  .
. ; б)
; б) 
 ; б)
; б) 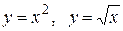 .
.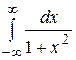 ; б)
; б) 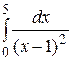 .
.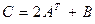





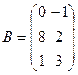

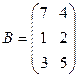







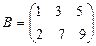


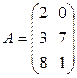











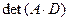 и
и  .
.

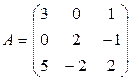







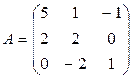




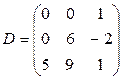




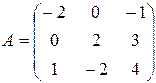





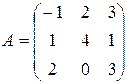


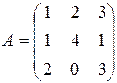



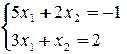
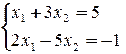


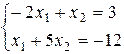







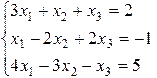



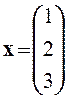



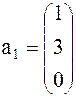


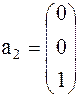

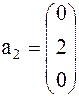

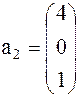

 . Составить: а) уравнения медианы и высоты треугольника
. Составить: а) уравнения медианы и высоты треугольника  , проведенные из вершины
, проведенные из вершины  ; б) уравнение биссектрисы внутреннего угла
; б) уравнение биссектрисы внутреннего угла  .
.