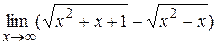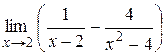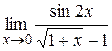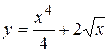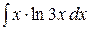Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Для специальности «Управление персоналом»Содержание книги
Поиск на нашем сайте
МАТЕМАТИКА Для специальности «Управление персоналом» Часть 1 Линейная алгебра и математический анализ
Учебно-методический комплекс
Авторы-составители д.т.н., профессор А.Н. Данчул, д.т.н., профессор В.М. Градов к.ф.-м.н., доцент Т.М. Поленова
Москва – 2011. Содержание ОСНОВНЫЕ ПОЛОЖЕНИЯ.. 3 УЧЕБНО-ТЕМАТИЧЕСКИЙ ПЛАН.. 4 СОДЕРЖАНИЕ ТЕМ.. 5 КОНТРОЛЬНЫЕ ЗАДАНИЯ.. 17 Таблица вариантов. 18 Контрольное задание №1. 19 Контрольное задание №2. 24 ВОПРОСЫ К ЭКЗАМЕНУ.. 28 ПРИЛОЖЕНИЕ. ОБРАЗЕЦ ОФОРМЛЕНИЯ ТИТУЛЬНОГО ЛИСТА КОНТРОЛЬНОГО ЗАДАНИЯ.. 32 ОСНОВНЫЕ ПОЛОЖЕНИЯ
Программа части 1 Линейная алгебра и математический анализ учебной дисциплины «Математика» разработана в соответствии с требованиями Государственного образовательного стандарта профессионального высшего образования для обучения студентов специальности «Управления персоналом». Целью изучения дисциплины является подготовка студентов к творческому восприятию последующих общепрофессиональных и специальных дисциплин. Студенты должны научиться владеть современным математизированным профессиональным языком, принятым в мировом научном сообществе, знать основные возможности и ограничения применения математического аппарата в профессиональной деятельности, а также иметь базовые навыки использования математического инструментария. Часть 1 Линейная алгебра и математический анализ дисциплины «Математика» направлена на достижение вышеуказанных целей в области линейной алгебры и математического анализа, создание фундамента для изучения последующих частей дисциплины (теория вероятностей и математическая статистика). Часть 1 Линейная алгебра и математический анализ дисциплины «Математика» читается в I семестре, рассчитана на 136 часов занятий, из которых 34 часа – лекции, 34 часов – практические занятия и 68 часов – самостоятельные занятия. Она не требует предварительных знаний, выходящих за рамки программы полной средней школы. По части 1 Линейная алгебра и математический анализ дисциплины «Математика» предусмотрены 2 контрольных задания. Формой итогового контроля работы студентов является экзамен. В экзаменационный билет входят два теоретических вопроса и одна задача из числа включенных в планы практических занятий или контрольные задания.
Требования к уровню освоения дисциплины включают знание определений рассматриваемых понятий, понимание формулировок и идей доказательств используемых теорем, знание доказательств основных теорем, излагаемых на лекциях, уверенное владение методами решения задач, содержащихся в планах практических занятий.
УЧЕБНО-ТЕМАТИЧЕСКИЙ ПЛАН
СОДЕРЖАНИЕ ТЕМ
Тема 1. Матрицы и определители
Понятие матрицы. Определение и виды прямоугольных матриц. Векторы. Операции над матрицами. Определитель квадратной матрицы. Минор. Алгебраическое дополнение. Разложение определителя по строке или столбцу. Свойства определителей. Элементарные преобразования строк и столбцов матрицы. Обратная матрица. Ранг матрицы.
Тема 2. Системы линейных алгебраических уравнений
Системы линейных алгебраических уравнений. Запись и решение системы линейных алгебраических уравнений в матричном виде. Формулы Крамера. Теорема Кронекера-Капелли о разрешимости системы. Решение системы линейных алгебраических уравнений, матричных уравнений и вычисление обратной матрицы методом Гаусса.. Общее решение системы линейных алгебраических уравнений; свободные неизвестные, базисные решения.
Тема 3. Линейные пространства и преобразования
Векторы на плоскости и в трехмерном пространстве. Определение и примеры линейного пространства. Линейная зависимость и независимость векторов. Базис. Координаты. Размерность. Преобразование координат при переходе к новому базису. Скалярное произведение. Ортонормированный базис. Евклидовы пространства.
Линейные преобразования (операторы). Способы нахождения матрицы линейного преобразования.
Тема 4. Комплексные числа. Собственные значения и векторы
Определение, геометрическая интерпретация и формы записи комплексных чисел. Операции над комплексными числами и их свойства. Возведение в степень и извлечение корня из комплексного числа. Собственные значения и собственные векторы матриц, их нахождение. Свойства собственных векторов.
Тема 5. Элементы аналитической геометрии
Уравнения прямой на плоскости. Уравнения прямой и плоскости в трехмерном пространстве. Условия параллельности и перпендикулярности. Угол между прямыми. Расстояние от точки до прямой. . Тема 6. Числовые последовательности. Функции одной переменной. Пределы последовательностей и функций Понятие числовой последовательности. Предел последовательности. Основные свойства сходящихся последовательностей. Признаки существования предела последовательности. Понятие действительной функции действительной переменной. Способы задания функции. График функции. Основные элементарные функции. Сложные и взаимно обратные функции. Неявные функции. Алгебраические и трансцендентные функции. Основные свойства функций. Предел функции в бесконечности и в точке. Односторонние пределы. Признаки существования предела функции. Бесконечно малые и бесконечно большие величины. Два замечательных предела. Непрерывность функции в точке. Свойства функций, непрерывных в точке и на отрезке. Тема 7. Дифференциальное исчисление Производная функции и дифференциал. Геометрический и физический смысл производной; геометрический смысл дифференциала. Правила дифференцирования сумм, произведения и частного функций. Производная сложной и обратной функций. Производные основных элементарных функций. Производные высших порядков. Теоремы Ферма, Ролля и Лагранжа. Правило Лопиталя. Точки экстремума, выпуклость и точки перегиба функции. Асимптоты. Общая схема исследования функций. Уравнение касательной и нормали к графику функции.
Тема 8. Неопределенный и определенный интегралы Первообразная и неопределенный интеграл. Свойства неопределенного интеграла. Интегралы от основных элементарных функций. Основные методы интегрирования. Интегрирование рациональных дробей. Понятие и геометрическая интерпретация определенного интеграла. Свойства определенного интеграла. Формула Ньютона-Лейбница. Несобственные интегралы с бесконечными пределами интегрирования и несобственные интегралы от неограниченных функций. Признаки сходимости несобственных интегралов
Тема 1. Матрицы и определители Занятие 1 1. Повторение определений основных понятий темы. 2. Даны матрицы A и B. а) Указать, какие из нижеприведенных операций выполнимы, и выполнить их. а) A + B; б ) AT + B; в) A + B T; г) AT + B T. д) AB; е) ATB; ж) AB T; з) BAT. На дом а) 3. Решить задачи [Л1[1], с.60, 64]: 1.17, 1.20, 1.23; 1.40, 1.43 На дом 1.18, 1.21, 1.25; 1.42, 1.45 4. Найти определитель матрицы
Занятие 2 1. Повторение определений основных понятий темы.
2. Решить задачи [Л1, с.65, 68]: 1.51; 1.62 на дом 1.52; 1.65. 3. Найти матрицу, обратную матрице С, если она существует (см. п. 4 занятия 1).
4. Найти ранг матриц
5. Решить задачи [Л1, с.70-71]: 1.71; 1.73; 1.79 на дом 1.74; 1.75; 1.82.
Занятие 1 1. Повторение определений основных понятий темы. 2. Решить задачи [Л1, с. 108]: 2.14, 2.19, 2.22 на дом 2.15, 2.20, 2.23. 3. Решить системы уравнений методом Гаусса а) на дом а) 4. Решить задачу 2.46 [Л1, с. 115]: Занятие 2 1. Повторение определений основных понятий темы. 2. Решить задачи [Л1, с. 108, 115]: 2.261, 2.47; на дом 2.271, 2.48. 3. Найти базисные и общее решения системы уравнений из задач [Л1, с. 115-116]. 2.52, 2.54; на дом 2.53; 2.55. Занятие 3 1. Повторение определений основных понятий темы. 2. Решить задачи [Л1, с. 117-119]: 2.67, 2.69; на дом 2.68; 2.70, 2.72. Тема 3. Линейные пространства и преобразования Занятие 1 1. Повторение определений основных понятий темы. 2. Доказать, что множество двухмерных геометрических векторов с заданными на нем операциями сложения и умножения на число образует линейное пространство. 3. Решить задачи [Л1, с. 165-166]: 3.50, 3.53, 3.56, 3.58, 3.61 на дом 3.51, 3.54, 3.57, 3.59, 3.62. 4. Найти косинус угла между векторами x и y, принадлежащими трехмерному евклидову пространству с ортонормированным базисом. а) 5. Решить задачи [Л1, с. 158-159]: 3.20, 3.26 на дом 3.21, 3.27. Занятие 2 1. Повторение определений основных понятий темы. 2. Решить задачи [Л1, с. 168-169]: 3.71, 3.78 на дом 3.72, 3.79.
вектор
4. Найти матрицу линейного преобразования, переводящего каждый вектор x двухмерного векторного пространства в вектор y по следующему алгоритму. а) симметричное отображение относительно прямой x1= x2; б) поворот на 45° по часовой стрелке; в) симметричное отображение относительно прямой x1= 0, а затем симметричное отображение относительно начала координат. на дом а) симметричное отображение относительно прямой x1= -x2. б) поворот на угол α против часовой стрелки; в) симметричное отображение относительно начала координат, а затем симметричное отображение относительно прямой x2= 0. 5. Решить задачи [Л1, с. 169]: 3.80 на дом 3.81. Занятие 1 1. Повторение определений основных понятий темы. 2. Решить задачи [Л1, с. 805-806]: 15.7, 15.8в, 15.12; 15.22 на дом 15.8г, 15.23. Даны комплексные числа 4. Решить задачи [Л1, с. 172-173]: 3.87, 3.91, 3.96, 3.98 на дом 3.88, 3.92, 3.97, 3.99.
Занятие 2 1. Повторение определений основных понятий темы. 2. Решить задачи [Л1, с. 172-173]: 3.87, 3.91, 3.96, 3.102 на дом 15.8г, 15.23.
Занятие 1 1. Повторение определений основных понятий темы. 2. Решить задачи [Л1, с. 217-218]: 4.21, 4.35, 4.37, 4.38, 4.47 на дом 4.28, 4.39, 4.41, 4.48. Занятие 2 1. Повторение определений основных понятий темы. 2. Решить задачи [Л1, с. 235]: 4.114а, 4.115, 4.117 на дом 4.114б, 4.116, 4.119.
Тема 6. Числовые последовательности. Функции одной переменной. Пределы последовательностей и функций Занятие 1 1. Повторение определений основных понятий темы. 2. Определить области существования и области значений следующих функций: а) на дом а) 2. Построить график функции
3. Решить задачи [Л1, с.267]: 5.38(а, в); 5.39(а, г); 5.40(а); 5.41(а) на дом 5.38(б, г), 5.39(б, д); 5.40(б, в), 5.41(б). 4. Найти: а) на дом 5. Решить задачи [Л1, с.296, 297, 302]: 6.8(а, б); 6.9(а) на дом 6.15; 6.21. Занятие 2 1. Повторение определений основных понятий темы. 2. Вычислить пределы а) 3. Решить задачи [Л1, с.298 – 304]: 6.10(а, г, д); 6.11(г, б) на дом 6.23; 6.39; 6.41; 6.47; 6.49; 6.63; 6.69. 4. Решить задачи [Л1, с.305 – 304]: 6.80(б, в); 6.88; 6.109; 6.110 на дом 6.83; 6.85; 6.86; 6.111; 6.120.
КОНТРОЛЬНЫЕ ЗАДАНИЯ Выполняются два контрольных задания по 6 задач в каждом. По выданному преподавателем номеру варианта задания с помощью таблицы вариантов, приведенной на следующей странице, определяются номера варианты входящих в задание задач. Образец оформления титульного листа задания приведен в Приложении. Сроки сдачи заданий: · задание 1 – 10 неделя (до 8 ноября); · задание 2 – 16 неделя (до 20 декабря). Сроки зачета заданий (с учетом исправления ошибок): · задание 1 – 11 неделя (до 15 ноября); · задание 2 – 17 неделя (до 27 декабря). Таблица вариантов
Контрольное задание №1 Задача 1. Даны матрицы A и B. Найти матрицу Вариант 1 Вариант 2
Вариант 3 Вариант 4
Вариант 5 Вариант 6
Вариант 7 Вариант 8
Вариант 9 Вариант 10
Задача 2. Найти матрицу, обратную матрице
Задача 4. Найти определитель произведения двух матриц Вариант 1 Вариант 2 Вариант 3 Вариант 4 Вариант 5 Вариант 6 Вариант 7 Вариант 8 Вариант 9 Вариант 10 Задача 4. Найти ранг матрицы
Задача 5. Записать систему уравнений в матричном виде и решить ее как матричное уравнение. Вариант 1 Вариант 2 Вариант 3
Вариант 4 Вариант 5 Вариант 6
Вариант 7 Вариант 8 Вариант 9
Вариант 10
Задача 6. Решить систему уравнений методом Гаусса Вариант 1 Вариант 2 Вариант 3
Вариант 4 Вариант 5 Вариант 6
Вариант 7 Вариант 8 Вариант 9
Вариант 10
Контрольное задание №2
Задача 1. Представить вектор x в виде линейной комбинации векторов a1, a2, a3, если система векторов a1, a2, a3 линейно независима. В случае линейной зависимости векторов a1, a2, a3 заменить один из них на вектор x так, чтобы полученная система стала линейно независимой.
Вариант 1 Вариант 2
Вариант 3 Вариант 4
Вариант 5 Вариант 6
Вариант 7 Вариант 8
Вариант 9 Вариант 10
Задача 2. Найти матрицу линейного преобразования, переводящего каждый вектор x двухмерного линейного пространства в вектор y по следующему алгоритму:
Задача 3. Даны вершины треугольника
Задача 4. Вычислить пределы функций
Задача 5. Исследовать функцию и построить график.
Задача 6. Найти неопределенный интеграл.
ВОПРОСЫ К ЭКЗАМЕНУ 1. Матрицы и основные операции над ними. 2. Виды матриц. Геометрическая интерпретация векторов. 3. Умножение матриц. 4. Определители матриц второго и третьего порядка. 5. Обратная матрица и ее нахождение. 6. Свойства определителей. 7. Элементарные преобразования строк и столбцов матрицы. Их использование при нахождении определителей. 8. Ранг матрицы. Способы вычисления ранга матрицы. 9. Теорема Кронекера-Капелли совместимости системы линейных алгебраических уравнений. 10. Запись и решение системы линейных алгебраических уравнений в матричном виде. 11. Решение системы линейных алгебраических уравнений методом Гаусса. 12. Вычисление обратной матрицы методом Гаусса. 13. Общее решение системы линейных алгебраических уравнений; свободные неизвестные, базисные решения. 14. Линейное пространство. 15. Линейная зависимость и независимость векторов. Способы определения. 16. Базис линейного пространства. Размерность линейного пространства 17.. Преобразование координат при переходе к новому базису. 18. Скалярное произведение векторов. Угол между векторами 19.. Ортонормированный базис. Евклидово пространство 20. Линейные преобразования. Свойства. 21. Нахождение матрицы линейного преобразования. 22..Определение, геометрическая интерпретация и формы записи комплексных чисел. 23. Операции над комплексными числами. 24. Собственные значения и собственные векторы матриц, свойства собственных векторов. 25. Уравнения прямой в двухмерном пространстве 26. Условия параллельности и перпендикулярности 27. Уравнения прямой в трехмерном пространстве 28. Уравнения плоскости в трехмерном пространстве 29. Понятие действительной функции действительной переменной. Способы задания функции. График функции. 30. Основные элементарные функции. Сложная и взаимно обратные функции. 31. Основные свойства функций. 32. Понятие числовой последовательности и основные свойства сходящихся последовательностей. 33. Предел числовой последовательности. Признаки существования предела последовательности. Два замечательных предела. 34. Предел функции в бесконечности и в точке. 35. Непрерывность функции действительной переменной в точке и на отрезке. 36. Свойства функций, непрерывных на отрезке. 37. Производная функции и дифференциал. 38. Производные и дифференциалы высших порядков. 39. Геометрический и физический смысл производной; геометрический смысл дифференциала. 40. Правила дифференцирования сумм, произведения и частного функций. Производная сложной и обратной функций. 41. Теоремы Ферма, Ролля, Лагранжа. 42. Правило Лопиталя. 43. Точки экстремума. Необходимое и достаточное условие локального экстремума функции. 44. Выпуклость и точки перегиба функции. Необходимое и достаточное условие перегиба функции. 45. Нахождение асимптот функции. 46. Уравнения касательной и нормали к графику функции в заданной точке. 47. Первообразная функции и неопределенный интеграл. 48. Свойства неопределенного интеграла. 49. Интегрирование рациональных дробей. 50. Понятие определенного интеграла. Свойства определенного интеграла. 51. Формула Ньютона-Лейбница. 52. Несобственные интегралы с бесконечными пределами. Признаки сходимости несобственных интегралов. 53. Несобственные интегралы от неограниченных функций. Признаки сходимости несобственных интегралов. 54. Геометрические приложения определенного интеграла.. ПРИЛОЖЕНИЕ.
Российская академия государственной службы при Президенте РФ
Задание N 1 по математике
Слушателя группы О-811 Иванова Петра Фомича Вариант 15
Г. [1] Л1 – литература под номером 1 в списке литературы 1 Ответ в [Л1] – неверный. [2] - множество действительных чисел. МАТЕМАТИКА для специальности «Управление персоналом» Часть 1
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 387; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.74.100 (0.012 с.) |




 на дом
на дом 



 ; б)
; б)  .
.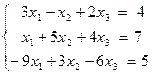 ; б)
; б) 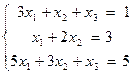
 ,
,  б)
б)  ,
,  .
.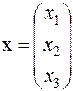 в вектор
в вектор 
 на дом
на дом  .
.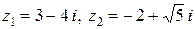 . Представить в тригонометрической форме и экспоненциальной форме и изобразить на комплексной плоскости эти числа, а также
. Представить в тригонометрической форме и экспоненциальной форме и изобразить на комплексной плоскости эти числа, а также 
 ; б)
; б) 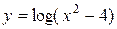 ; в)
; в) 
 ; б)
; б) 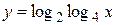 ; в)
; в)  .
.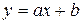 ,
,  [2].
[2].
 , если
, если  ; б)
; б) 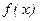 , если
, если  ;
; , если
, если 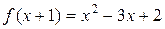 .
.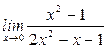 ; б)
; б)  ; в)
; в) 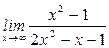 .
.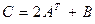





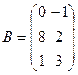

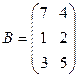







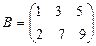


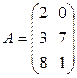











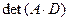 и
и  .
.

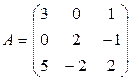







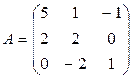




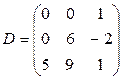




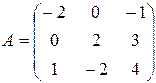





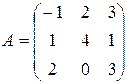


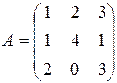



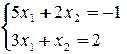
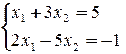


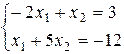







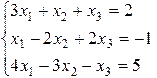



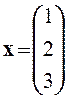



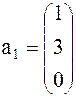


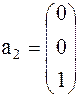

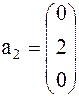

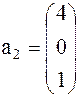

 . Составить: а) уравнения медианы и высоты треугольника
. Составить: а) уравнения медианы и высоты треугольника  , проведенные из вершины
, проведенные из вершины  ; б) уравнение биссектрисы внутреннего угла
; б) уравнение биссектрисы внутреннего угла  .
.