
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Механический смысл производнойСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Пусть материальная точка движется по прямой по закону S = S (t),
тогда D S = S (t+ D t) – S (t) – расстояние, пройденное за время D t и средняя скорость движения:
Чтобы найти скорость движения в момент времени t, надо рассмотреть предел V (t) = Производная от пути S (t) равна мгновенной скорости точки в момент времени t:
Геометрический смысл производной Точка M 0(x 0; y (x 0)) – фиксированная точка графика
Рис. 5 Рассмотрим треугольник M 0 MA: tg j = Перейдем к пределу при D x ®0:
где Уравнение касательной к линии y = f (x) в точке M 0(x 0; f (x 0)): y = f (x 0) + f ' (x 0) × (x – x 0). Нормаль – прямая, перпендикулярной касательной и проходящей через точку касания M0(x 0; f (x 0)): y = f (x 0) –
6. Производная обратной функции. Производная сложной функции Для дифференцируемой функции с производной, отличной от нуля, производная обратной функции равна обратной величине производной данной функции, т.е
·
(производная сложной функции). Если функция f (u) дифференцируема в точке u, а функция u (x) дифференцируема в точке x, причём u = u (x), тогда сложная функция f (u (x)) дифференцируема в точке x и её производная вычисляется по формуле: (f (u (x)))' = f '(u) × u ' (x). h (x) = g (f (x)). 7. Основные свойства производных. Производные элементарных Функций (c u) ’ = c u’, d (c u) = c du, (c – const); (u ± v) ’ = u’ ± v’, d (u ± v) = du ± dv; (u v) ’ = u’ v + u v’, d (u v) = v du + u dv;
Таблица производных основных элементарных функций 1. (c)' = 0 2. (x a)' = a× x a – 1 3. (ax)' = ax ×ln a, (a > 0, a ≠ 1) 4. (ex)' = ex 5. (lo ga x)' = 6. (ln x)' = 7. (sin x)' =cos x 8. (cos x)' = – sin x 9. (tg x)' = 10. (ctg x)' = – 11. (arcsin x)' = 12. (arccos x)' = – 13. (arctg x)' = (arcctg x)' = Производные и дифференциалы высших порядков Если функция y = f (x) дифференцируема на некотором промежутке, то она имеет на этом промежутке производную y ' = f ' (x), которая в свою очередь может иметь производную: (y ')' = (f '(x))' = y '', называемую второй производной функции y = f (x). Она обозначается:
Может случиться, что новая функция y ''(x) имеет производную, тогда она называется третьей производной функции y = f (x) и обозначается:
Производная “n”-го порядка функции y = f (x) обозначается:
Дифференциалом второго порядка функции y = f (x) в точке x называется выражение, обозначаемое d2 y и вычисляемое по формуле:
если x – независимая переменная. Дифференциал третьего порядка функции y = f (x):
если x – независимая переменная, и т.д. Замечание. Дифференциал уже второго порядка не обладает свойством инвариантности формы. Теорема Ролля Теорема 4 (теорема Ролля). Если функция f (x) определена на отрезке [ a; b ] и выполнены следующие условия: · f (x) непрерывна на отрезке [ a; b ]; · f (x) дифференцируема на интервале (a; b); · f (a) = f (b), то внутри этого отрезка [ a; b ] найдется хотя бы одна точка х 0, в которой выполняется равенство: f '(х 0) = 0. Теорема Лагранжа Теорема 5 (теорема Лагранжа). Если функция f (x) определена на отрезке [ a; b ] и выполнены следующие условия: · f (x) непрерывна на отрезке [ a; b ], · f (x) дифференцируема на интервале (a; b), то внутри этого отрезка существует хотя бы одна точка х 0, в которой выполняется равенство: f ' (х 0) =
Теорема Коши Теорема 6 (теорема Коши). Если функции f (x) и g (x) определены на отрезке [ a; b ] и удовлетворяют условиям: · f (x) и g (x) непрерывны на отрезке [ a; b ]; · f (x) и g (x) дифференцируемы на интервале (a; b); · g '(x) ¹ 0 при любом x Î (a; b), то внутри отрезка [ a; b ] найдётся хотя бы одна точка х 0, в которой выполняется равенство:
Правило Лопиталя Теорема 7 (правило Лопиталя). Если функции f (x) и g (x) определены в некоторой окрестности точки х 0 и в этой окрестности они удовлетворяют условиям: · f (x) и g (x) дифференцируемы в каждой точке за исключением может быть самой точки х 0; · g '(x) ¹ 0 для любого x из этой окрестности; · тогда, если существует
Замечание 1. Правило Лопиталя используется для раскрытия неопределённостей типа
Замечание 2. Если к условиям теоремы 7 добавить дифференцируемость функций f '(x) и g '(x) в окрестности точки х 0, то при выполнении остальных требований для f '(x) и g '(x) правило Лопиталя можно применить повторно.
|
||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 496; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.52.58 (0.011 с.) |


 .
. при D t ® 0:
при D t ® 0: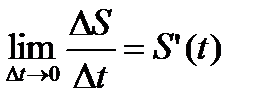 .
. .
. . Точка M (x 0+D x; y (x 0+D x)) при различных значениях D x – любая точка на графике. Если точка M приближается к точке M 0 (при этом D x ® 0), то секущая линия M 0 M стремится к своему предельному положению, называемому касательной к линии y = f(x) в точке M 0.
. Точка M (x 0+D x; y (x 0+D x)) при различных значениях D x – любая точка на графике. Если точка M приближается к точке M 0 (при этом D x ® 0), то секущая линия M 0 M стремится к своему предельному положению, называемому касательной к линии y = f(x) в точке M 0.
 , j – угол наклона секущей M 0 M к оси Ox.
, j – угол наклона секущей M 0 M к оси Ox. j =
j =  ,
, – угол наклона касательной к оси Ox.
– угол наклона касательной к оси Ox. ,
,

 ,
,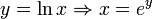 ,
,
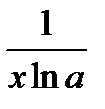 , (a > 0; a ≠ 1)
, (a > 0; a ≠ 1)


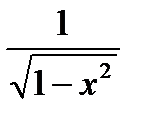






 ,
, ,
, .
. .
. или
или  ,
,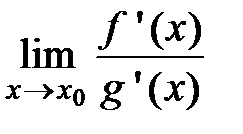 конечный или бесконечный, то выполняется равенство:
конечный или бесконечный, то выполняется равенство: =
=  .
. или
или  , возникающих при вычислении пределов. Если под знаком предела оказывается неопределённость другого типа: 0×∞,
, возникающих при вычислении пределов. Если под знаком предела оказывается неопределённость другого типа: 0×∞,  , 10, 00 или ∞0, то с помощью тождественных алгебраических преобразований такая неопределённость приводится к
, 10, 00 или ∞0, то с помощью тождественных алгебраических преобразований такая неопределённость приводится к 


