
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Наибольшее и наименьшее значения функции на отрезкеСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Пусть функция y = f (x) определена на отрезке [ a; b ]. Определение 10. Число f (c) называется наибольшим (наименьшим) значением функции y = f (x) на отрезке [ a; b ] и обозначается f (x) £ f (c) (f (x) ³ f (c)). Если функция y = f (x) непрерывна на отрезке [ a; b ], то по свойству непрерывной на отрезке функции она достигает своих наибольшего и наименьшего значений. Схема нахождения этих значений следующая: 1) Найти все точки, в которых f '(x) = 0 (или не существует). Причём выбрать те точки из полученных, которые попадают на отрезок [ a; b ]. 2) Вычислить значения функции в полученных точках в п.1. 3) Вычислить значения функции в граничных точках отрезка [ a; b ]: f (a) и f (b). 4) Из значений п.2 и п.3 найти наибольшее число M и наименьшее m. Тогда Функции нескольких переменных. Основные понятия. Определение. Если каждой паре (x,y) значений двух независимых друг от друга, переменных величин x и y, из некоторой области их изменения D, соответствует определенное значение величины z, то говорят, что z функция двух независимых переменных x и y, определенная в области D.
Частные производные. Определение. Частной производной по x от функции z=f(x,y) называется предел отношения частного приращения Частная производная обозначается одним из символов Аналогично определяется частная производная по y: Таким образом, частные производные функции двух переменных вычисляются по тем же правилам, что и производные функции одного переменного. Частные производные функции любого числа переменных определяют 3. Геометрическая интерпретация частных производных функции двух Переменных
Аналогично, частная производная плоскостью x=const.
13. Полный дифференциал функции нескольких переменных, его применение в приближённых вычислениях, достаточное условие дифференцируемости. Формула полного дифференциала функции нескольких переменных:
d2z=z’x’x*d2x+ z’y’y*d2y Формула приближенного вычисления: z=z(x, y); Dz = dz; dx=Dx; dy=Dy z (x, y)»z(M0)+z’x(M0)*Dx+ z’y(M0)*Dy Достаточное условие дифференцируемости: Если функция z=(x; у) имеет непрерывные частные производные 14. Уравнения касательной плоскости и нормали к поверхности. Дифференцирование сложных и неявных функций. (неявная функция) (явная функция) Уравнение касательной: F’x(M0)*(x-x0)+ F’y(M0)*(y-y0)+ F’z(M0)*(z-z0)=0 z’x(M0)*(x-x0)+ z’y(M0)*(y-y0)=(z-z0) Уравнение нормали: N̅={F’x; F’y; F’z} N̅={z’x; z’y -1} (x-x0)/ F’x(M0)= (y-y0)/ F’y(M0)= (z-z0)/ F’z(M0) (x-x0)/ z’x(M0)= (y-y0)/ z’y(M0)= (z-z0)/ (-1) Дифференцирование: (сложные функции) (неявной функции F(x, y, z)=0) 1. z=z(x, y), x=x(t) => z=z(t)) z’x= -(F’x/F’z) y=y(t) z’y= -(F’y/F’z) dz/dt=z’x*x’t+ z’y*y’t 2. z=z(x, y), y=y(x) => z=z(x) dz/dx=z’x+ z’y*y’x 3. z=z(x, y), x=x(u, v) => z=z(u, v) y=y(u, v) ∂z/∂u= z’u= z’x*x’u+ z’y*y’u ∂z/∂v= z’v= z’x*x’v+ z’y*y’v 15. Производные высших порядков функции нескольких переменных. z=z(x, y) z’x, z’y – первого порядка z’x’x, z’y’y, z’x’y, z’y’x – второго порядка z’x’y= z’y’x 16. Экстремум функции нескольких переменных. Необходимое и достаточное условия экстремума. 1. Найти частные производные z’x и z’y. Составить и решить систему уравнений z’x=0 z’y=0 Точки, координаты которых удовлетворяют указанной системе, называют стационарными. 2. Найти А=z’x’x, С=z’y’y, В=z’x’y и вычислить значение Δ=А*С-В2 в каждой стационарной точке. После этого использовать следующую схему: · Если Δ>0 и А>0, то в исследуемая точка есть точкой минимума. · Если Δ>0 и А<0, то в исследуемая точка есть точкой максимума. · Если Δ<0, то в рассматриваемой стационарной точке экстремума нет. · Если Δ=0, то ничего определённого про наличие экстремума сказать нельзя; требуется дополнительное исследование.
|
||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 660; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.242.39 (0.006 с.) |

 (
( ), если для любого x Î [ a; b ] выполняется неравенство:
), если для любого x Î [ a; b ] выполняется неравенство: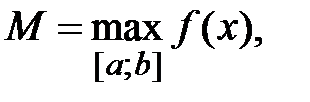


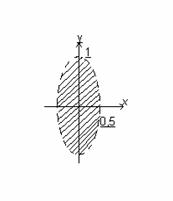 Для функции трех переменных областью определения является упорядоченная тройка чисел (x,y,z), т.е. некоторая совокупность точек пространства. Функции двух переменных допускают графическую иллюстрацию. Графиком функции z = f(x,y), заданной на некотором множестве D точек плоскости ХОУ, называется множество точек (x,y,z) пространства, у которых (x,y) принадлежит D, а z = f (x,y). В наиболее простых случаях такой график представляет собой некоторую поверхность.
Для функции трех переменных областью определения является упорядоченная тройка чисел (x,y,z), т.е. некоторая совокупность точек пространства. Функции двух переменных допускают графическую иллюстрацию. Графиком функции z = f(x,y), заданной на некотором множестве D точек плоскости ХОУ, называется множество точек (x,y,z) пространства, у которых (x,y) принадлежит D, а z = f (x,y). В наиболее простых случаях такой график представляет собой некоторую поверхность. по x к приращению
по x к приращению  при стремлении
при стремлении 
 .
.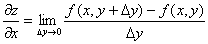 .
. Частная производная
Частная производная  численно равна тангенсу угла наклона касательной к кривой, получающейся в сечении поверхности z=f(x,y) плоскостью x=const.
численно равна тангенсу угла наклона касательной к кривой, получающейся в сечении поверхности z=f(x,y) плоскостью x=const. численно равна тангенсу угла наклона касательной к кривой, получающейся сечении поверхности z=f(x,y)
численно равна тангенсу угла наклона касательной к кривой, получающейся сечении поверхности z=f(x,y) или dz=z’x*dx+ z’y*dy или du=u’x*dx+ u’y*dy+ u’z*dz
или dz=z’x*dx+ z’y*dy или du=u’x*dx+ u’y*dy+ u’z*dz и
и  в точке М(х;у), то она дифференцируема в этой точке.
в точке М(х;у), то она дифференцируема в этой точке.


