
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция № 2. Соответствия и функции.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
1. Соответствия. Определение. Соответствием между множествами А и В называется некоторое подмножество G их декартова произведения: Если В принятых обозначениях, каждый элемент Соответствие называется полностью определённым, если Соответствие Соответствие Соответствие называется инъективным, если оно является функциональным, и при этом каждый элемент множества Соответствие Пример 1. а) Англо-русский словарь устанавливает соответствие между множествами слов русского и английского языка. Оно не является функциональным, так как почти каждому русскому слову соответствует несколько английских переводов; оно, также, не является, как правило, полностью определённым соответствием, так как всегда существуют английские слова, не включённые в данный словарь. Таким образом, это частичное соответствие. б) Соответствие между аргументами функции в) Соответствие между расположенными на шахматной доске фигурами и занимаемыми ими полями является взаимно однозначным. г) Соответствие между телефонами города Вязьмы и их пятизначными номерами обладает, на первый взгляд, всеми свойствами взаимнооднозначного соответствия. Однако оно, например, не сюръективно, поскольку существуют пятизначные числа, не соответствующие никаким телефонам.
2. Взаимнооднозначные соответствия и мощности множеств.
Если между двумя конечными множествами А и В существует взаимнооднозначное соответствие, то эти множества равномощны. Этот очевидный факт позволяет, во-первых, установить равенство мощности этих множеств, не вычисляя их. Во-вторых, часто можно вычислить мощность множества, установив его однозначное соответствие с множеством, мощность которого известна, либо легко вычисляется. Теорема 2.1. Если мощность конечного множества А равна Множество всех подмножеств множества М называется булеаном и обозначается Определение. Множества А и В называются равномощными, если между их элементами можно установить взаимнооднозначное соответствие. Заметим, что для конечных множеств это утверждение легко доказать. Для бесконечных множеств оно определят само понятие равномощности. Определение. Множество А называется счётным, если оно равномощно множеству натуральных чисел Очень упрощённо можно сказать, что данное бесконечное множество является счётным, если для его элементов можно установить нумерацию с помощью натуральных чисел. Без доказательства примем ряд важных фактов: 1. Любое бесконечное подмножество множества натуральных чисел является счётным. 2. Множество 3. Множество рациональных чисел 4. Объединение конечного числа счётных множеств является счётным. 5. Объединение счётного числа конечных множеств является счётным. 6. Объединение счётного числа счётных множеств является счётным. Все эти утверждения, как можно видеть, позволяют достаточно успешно устанавливать факт, что данное множество является счётным. Однако сейчас будет показано, что не всякое бесконечное множества является счётным; существует множества большей мощности. Теорема 2.2 (теорема Кантора). Множество всех действительных чисел из отрезка Доказательство. Допустим, что множество
Теперь рассмотрим любую бесконечную десятичную дробь вида Следствие 1. Множество действительных чисел Следствие 2. Множество всех подмножеств счётного множества континуально. Как показывается в теории множеств (с помощью метода, аналогичного приведённому выше), для множества любой мощности множество всех его подмножеств (булеан) имеет более высокую мощность. Поэтому не существует множества максимальной мощности. Например, множество-универсум
3. Отображения и функции. Функцией называется любое функциональное соответствие между двумя множествами. Если функция Полностью определённая функция Если Отображение типа Пример 2. а) Функция б) Функция в) Функция г) Функция Определение. Функция типа Например, сложение, умножение, вычитание и деление являются двухместными функциями на Определение. Пусть дано соответствие Определение. Если соответствие, обратное к функции Очевидно, что в обратном соответствии образы и прообразы меняются местами, поэтому для существования обратной функции Пример 3. Функция Определение. Пусть даны функции Композиция функций Для многоместных функций Например, в математическом анализе вводится понятие элементарной функции, являющейся суперпозицией фиксированного (не зависящего от значения аргумента) числа арифметических операций, а также элементарных функций ( А.Н. Колмогоровым и В.И. Арнольдом доказано, что всякая непрерывная функция Замечание. Понятие функции широко используется в математическом анализе, более того, является в нём базовым понятием. В целом, подход к пониманию термина “функция” в матанализе несколько уже, чем в дискретной математике. Как правило, в нём рассматриваются так называемые вычислимые функции. Функция называется вычислимой, если задана процедура, позволяющая по любому заданному значению аргумента найти значение функции.
Назад, в начало конспекта.
|
||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 2261; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.33 (0.008 с.) |

 .
.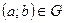 , то говорят, что
, то говорят, что 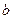 соответствует
соответствует 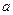 при соответствии
при соответствии 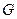 . При этом множество всех таких
. При этом множество всех таких  , а множество соответствующих значений
, а множество соответствующих значений 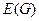 .
.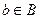 , соответствующий данному элементу
, соответствующий данному элементу  называется образом
называется образом  , то есть каждый элемент множества
, то есть каждый элемент множества  имеет хотя бы один образ во множестве
имеет хотя бы один образ во множестве 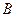 ; в противном случае соответствие называется частичным.
; в противном случае соответствие называется частичным.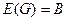 , то есть если каждому элементу множества
, то есть если каждому элементу множества 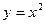 и значениями этой функции является функциональным. Однако оно не является взаимнооднозначным, так как каждому значению функции
и значениями этой функции является функциональным. Однако оно не является взаимнооднозначным, так как каждому значению функции 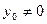 соответствуют два прообраза
соответствуют два прообраза 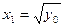 и
и 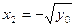 .
.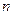 , то число всех подмножеств А равно
, то число всех подмножеств А равно  , то есть
, то есть 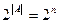 .
.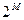 . Для конечных множеств выполняется:
. Для конечных множеств выполняется:  .
.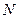 :
:  .
.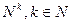 является счётным.
является счётным. является счётным (является следствием из предыдущего утверждения).
является счётным (является следствием из предыдущего утверждения).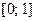 не является счётным.
не является счётным. является счётным и существует его нумерация. Поскольку любое действительное число можно представить в виде бесконечной десятичной дроби (периодической или непериодической), то проделаем это с числами данного множества. Расположим их в порядке этой нумерации:
является счётным и существует его нумерация. Поскольку любое действительное число можно представить в виде бесконечной десятичной дроби (периодической или непериодической), то проделаем это с числами данного множества. Расположим их в порядке этой нумерации:
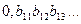 , организованную таким образом, что
, организованную таким образом, что 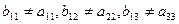 и так далее. Очевидно, что данная дробь не входит в рассматриваемую последовательность, поскольку от первого числа она отличается первой цифрой после запятой, от второго – второй цифрой и так далее. Следовательно, мы получили число из данного интервала, которое не пронумеровано и, таким образом, множество
и так далее. Очевидно, что данная дробь не входит в рассматриваемую последовательность, поскольку от первого числа она отличается первой цифрой после запятой, от второго – второй цифрой и так далее. Следовательно, мы получили число из данного интервала, которое не пронумеровано и, таким образом, множество  не является счётным. Его мощность называется континуум, а множества такой мощности называются континуальными. Приведённый метод доказательства называется диагональным методом Кантора.
не является счётным. Его мощность называется континуум, а множества такой мощности называются континуальными. Приведённый метод доказательства называется диагональным методом Кантора.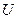 , описанное Кантором должно содержать все мыслимые множества, однако оно само содержится в множестве своих подмножеств в качестве элемента (парадокс Кантора). Получается, что множество
, описанное Кантором должно содержать все мыслимые множества, однако оно само содержится в множестве своих подмножеств в качестве элемента (парадокс Кантора). Получается, что множество 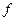 устанавливает соответствие между множествами А и В, то говорят, что функция
устанавливает соответствие между множествами А и В, то говорят, что функция 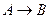 (обозначение
(обозначение 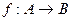 ). Каждому элементу
). Каждому элементу 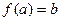 . Элемент
. Элемент 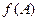 . Если при этом
. Если при этом 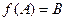 , то есть соответствие сюръективно, говорят, что имеет отображение А на В.
, то есть соответствие сюръективно, говорят, что имеет отображение А на В.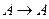 называется преобразованием множества А.
называется преобразованием множества А. является отображением множества натуральных чисел в себя (инъективная функция). Эта же функция при всех
является отображением множества натуральных чисел в себя (инъективная функция). Эта же функция при всех  является отображением множества целых чисел в множество рациональных чисел.
является отображением множества целых чисел в множество рациональных чисел.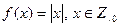 является отображением множества целых чисел (кроме числа 0) на множество натуральных чисел. Причём в данном случае соответствие не является взаимно однозначным.
является отображением множества целых чисел (кроме числа 0) на множество натуральных чисел. Причём в данном случае соответствие не является взаимно однозначным.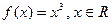 является взаимнооднозначным отображением множества действительных чисел на себя.
является взаимнооднозначным отображением множества действительных чисел на себя.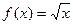 не полностью определена, если её тип
не полностью определена, если её тип 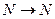 , но полностью определена, если её тип
, но полностью определена, если её тип 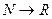 или
или  .
.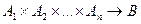 называется
называется 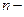 местной функцией. В этом случае принято считать, что функция имеет
местной функцией. В этом случае принято считать, что функция имеет 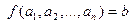 , где
, где  .
. .
. таково, что
таково, что  тогда и только тогда, когда
тогда и только тогда, когда  , то соответствие
, то соответствие 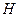 называют обратным к
называют обратным к 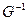 .
. требуется, чтобы каждый элемент из области значения
требуется, чтобы каждый элемент из области значения  имеет тип
имеет тип  . Отрезок
. Отрезок 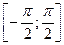 она взаимно однозначно отображает на отрезок
она взаимно однозначно отображает на отрезок 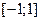 . Поэтому для неё на отрезке
. Поэтому для неё на отрезке 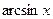 .
. . Функция
. Функция 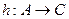 называется композицией функций
называется композицией функций 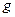 (обозначается
(обозначается 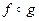 ), если имеет место равенство:
), если имеет место равенство:  , где
, где 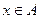 .
. получена подстановкой
получена подстановкой 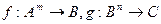 возможны различные варианты подстановок
возможны различные варианты подстановок  . В этом случае возможны, во-первых, любые подстановки функций друг в друга, а во-вторых, любые переименования аргументов. Функция, полученная из данных функций
. В этом случае возможны, во-первых, любые подстановки функций друг в друга, а во-вторых, любые переименования аргументов. Функция, полученная из данных функций 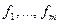 некоторой подстановкой их друг в друга и переименованием аргументов, называется их суперпозицией.
некоторой подстановкой их друг в друга и переименованием аргументов, называется их суперпозицией.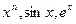 и т. п.).
и т. п.).


