
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция № 10. Булевы алгебры и теория множеств.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Определение. Функция Если взять отрицание обеих частей равенства и подставить Пример 1. Если рассматривать логические функции, то, очевидно, дизъюнкция двойственна конъюнкции и наоборот (непосредственно следует из правил Де Моргана). Отрицание является самодвойственной функцией. Функция-константа Пользуясь определением двойственности нетрудно доказать следующее утверждение, называемое принципом двойственности. Теорема 10.1. Если в формуле В булевой алгебре принцип двойственности имеет более конкретный вид, вытекающий из ранее приведённых примеров: если в формуле Если функции равны, то двойственные им функции также равны. Это позволяет с помощью принципа двойственности получать новые эквивалентные соотношения, переходя от равенства
Ранее были описаны булевы алгебры множеств, то есть алгебры вида Определение. Всякая алгебра типа В алгебре множеств элементами являются подмножества фиксированного универсального множества В одной из предыдущих лекций отмечалось взаимно однозначное соответствие между множеством Пусть даны два вектора
Поскольку компоненты (координаты) векторов принимают значения 0 или 1, то указанные операции – это просто логические операции над двоичными переменными, поэтому операции над векторами естественно назвать покомпонентными логическими операциями над двоичными векторами. Пример 2. Даны векторы Решение:
Заметим, что подобные операции (наряду с логическими операциями над переменными) входят в систему команд любой современной ЭВМ. Теорема 10.2. Если мощность множества Эта простая по содержанию теорема имеет огромное значение в математике. Она позволяет заменить теоретико-множественные операции над системой подмножеств данного множества поразрядными логическими операциями над двоичными векторами. Похожая по формулировке, но значительно отличающаяся по смыслу теорема существует для множества всех логических функций Теорема 10.3. Если мощность множества Теорема 10.3 указывает на тесную связь между множествами и логическими функциями и позволяет переходить от операций над множествами к операциям над функциями и обратно. В частности, они позволяют непосредственно производить операции над функциями, заданными не формулами, а таблицами. Пример приведён в следующей таблице, содержащей две функции трёх переменных
Теоретико-множественная интерпретация булевой алгебры предлагает очень удобный язык для изучения дизъюнктивных нормальных форм (ДНФ) и построения методов их упрощения. Рассмотрим кратко основные понятия, связанные с ДНФ. Введём следующее обозначение: обозначим через Если функция Пример 3. Рассмотрим функцию Прежде всего, заметим, что две переменных Далее, очевидно, что В рассматриваемом случае говорят, что конъюнкция Представление некоторой функции в виде ДНФ соответствует представлению её единичного множества в виде объединения интервалов; в совокупности все конъюнкции ДНФ покрывают всё единичное множество функции Назад, в начало конспекта.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 729; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.174.8 (0.006 с.) |

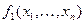 называется двойственной к функции
называется двойственной к функции  , если
, если  .
. вместо переменных
вместо переменных  , то получится
, то получится  . Это означает, что функция
. Это означает, что функция  двойственна к функции
двойственна к функции  , и, таким образом, отношение двойственности является симметричным. Из определения двойственности ясно, что для любой функции двойственная ей функция определяется однозначно. В частности, может оказаться, что функция двойственна самой себе. В этом случае она называется самодвойственной.
, и, таким образом, отношение двойственности является симметричным. Из определения двойственности ясно, что для любой функции двойственная ей функция определяется однозначно. В частности, может оказаться, что функция двойственна самой себе. В этом случае она называется самодвойственной. двойственна функции
двойственна функции  . Ещё один традиционный пример самодвойственной функции – функция
. Ещё один традиционный пример самодвойственной функции – функция  .
. , представляющей функцию
, представляющей функцию 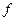 , все знаки функций заменить соответственно на знаки двойственных им функций, то полученная формула
, все знаки функций заменить соответственно на знаки двойственных им функций, то полученная формула  будет представлять функцию
будет представлять функцию  , двойственную функции
, двойственную функции  с помощью указанных замен к равенству
с помощью указанных замен к равенству  . Примером могут служить соотношения
. Примером могут служить соотношения  и
и 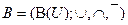 , где
, где  - булеан множества
- булеан множества 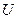 , то есть множество всех его подмножеств. Общий термин “булева алгебра” для алгебр множеств и логических функций не является случайным.
, то есть множество всех его подмножеств. Общий термин “булева алгебра” для алгебр множеств и логических функций не является случайным. называется булевой алгеброй, если её операции удовлетворяют соотношениям 1 – 10 (см. предыдущую лекцию).
называется булевой алгеброй, если её операции удовлетворяют соотношениям 1 – 10 (см. предыдущую лекцию). и множеством
и множеством  двоичных векторов длины
двоичных векторов длины 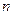 . Каждому подмножеству
. Каждому подмножеству  соответствует двоичный вектор
соответствует двоичный вектор  , где
, где 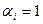 , если
, если  , и
, и  , если
, если  . Операции над векторами в булевой алгебре
. Операции над векторами в булевой алгебре  определяются следующим образом.
определяются следующим образом. и
и  из множества
из множества  ,
, ,
, .
. и
и 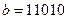 . Найти
. Найти  .
. .
. , то булева алгебра
, то булева алгебра  изоморфна булевой алгебре
изоморфна булевой алгебре  .
. . Обозначим это множество
. Обозначим это множество  . Оно замкнуто относительно операций
. Оно замкнуто относительно операций  и, следовательно, образует конечную булеву алгебру
и, следовательно, образует конечную булеву алгебру  , которая является подалгеброй булевой алгебры логических функций.
, которая является подалгеброй булевой алгебры логических функций.
 , то булева алгебра
, то булева алгебра 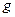 и результаты операций над ними:
и результаты операций над ними:





 множество всех единичных наборов функции
множество всех единичных наборов функции  из множества
из множества  . Множество
. Множество  переменных
переменных  , то
, то  двоичных наборов. Это объясняется тем, что в таком случае
двоичных наборов. Это объясняется тем, что в таком случае  переменных, не входящих в эту конъюнкцию несущественны для функции
переменных, не входящих в эту конъюнкцию несущественны для функции  и найдём её интервал.
и найдём её интервал. являются несущественными. Это позволяет сразу определить количество единичных наборов, содержащихся в множестве
являются несущественными. Это позволяет сразу определить количество единичных наборов, содержащихся в множестве  , то получим
, то получим  .
. только при значениях
только при значениях  . При этом переменные
. При этом переменные  могут принимать любые значения. Теперь перечислим все единичные наборы для данной функции:
могут принимать любые значения. Теперь перечислим все единичные наборы для данной функции:  . Итак,
. Итак,  .
. (или, точнее, интервал
(или, точнее, интервал  ) покрывает множество
) покрывает множество  принадлежат
принадлежат 


