
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция № 8. Логические функции.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Ниже будет подробно рассматриваться двухэлементное множество
Определение. Алгебра, образованная множеством Определение. Функцией алгебры логики (логической функцией) называется Первый термин является более точным, однако второй более распространён, особенно в приложениях. Он и будет использоваться в дальнейшем. Итак, логическая функция Определение. Алгебра, образованная Множество всех Всякая логическая функция Наборы, на которых значение функции равно 1, часто называют единичными наборами функции
Таблица 1. Заметим, что наборы в таблице расположены в определённом порядке – лексикографическом, который совпадает с возрастанием наборов, если рассматривать их как двоичные числа. Этим упорядочением будем пользоваться в дальнейшем. При любом фиксированном упорядочении наборов логическая функция Определение. Переменная Иначе говоря, переменная считается несущественной, если изменение её значения в любом наборе не изменяет значения функции. В этом случае функция Практический смысл удаления фиктивных переменных очевиден, поскольку они не влияют на значение функции и являются с этой точки зрения лишними. Однако иногда бывает полезно вводить фиктивные переменные. Благодаря такому введению можно всякую функцию
Логических функций одной переменной четыре; они приведены в таблице 2.
Таблица 2. Здесь функции
Логических функций двух переменных – шестнадцать; они приведены в таблице 3.
Таблица 3. Функции Среди представленных в таблице 3 функций отметим те, которые уже знакомы нам в качестве логических операций, изученных в ходе предыдущей лекции. Функция Операцию Функция Функция Привести пример такой функции более сложно. Для этого введём следующее понятие, широко используемое в теории чисел. Два целых числа Обозначается: Функция Функция Есть ещё две функции двух переменных, имеющие специальные названия. Функция В функциях Доказано, что с ростом числа переменных
Ранее было введено определение суперпозиции функций, согласно которому суперпозицией нескольких функций называлась новая функция, полученная с помощью подстановок данных функцией друг в друга и переименования переменных. Выражение, описывающее эту суперпозицию, называли формулой. Поскольку понятие суперпозиции является очень важным в алгебре логики, рассмотрим его более подробно. Пусть дано множество (конечное или бесконечное) исходных функций Определение. Говорят, что формула Соответственно, формулы В дальнейшем конкретные формулы будем записывать в более привычном виде, при котором условные знаки функций стоят между аргументами (такую запись называют инфиксной). Например, если Все формулы, построенные подобным образом, то есть содержащие только символы переменных, скобки и знаки функций из множества Возможны и другие интерпретации понятия глубины. Например, считается, что расстановка отрицаний над переменными не увеличивает глубины формулы. В случае, когда множество Всякая формула, выражающая данную функцию, как суперпозицию других функций, задаёт способ её вычисления (при условии, что известно, как вычислять исходные функции). Этот способ определяется следующим очевидным правилом: формулу можно вычислить, только если уже вычислены значения всех её подформул. Применим, например формулу Таким образом, формула ставит в соответствие каждому набору значений аргументов значение функции и, значит, может наряду с таблицей служить способом задания и вычисления функции. В частности, по формуле, вычисляя её на всех
В отличие от табличного задания представление данной функции формулой не единственно. Например, если в качестве исходного множества функций зафиксировать функции Определение. Формулы, представляющие одну и ту же функцию называются эквивалентными или равносильными. Эквивалентность формул принято обозначать знаком равенства, поэтому можно записать: Существует стандартный метод для выяснения эквивалентности двух формул. По каждой формуле восстанавливается таблица функции, а затем две полученные таблицы сравниваются. Таким способом в предыдущеё лекции мы устанавливали равносильность высказываний. Он весьма громоздок, так как требует Назад, в начало конспекта.
Лекция № 9. Булевы алгебры. В данной лекции будут рассмотрены способы представления логических функций в виде суперпозиций функций И, ИЛИ, НЕ.
Введём обозначения: Теорема 8.1. Всякая логическая функция
где Равенство (1) называется разложением по переменным
Практический смысл такого разложения очевиден: оно позволяет заменять функцию нескольких переменных суперпозицией конечного числа функций с меньшим количеством переменных. Особенно важен частный случай
где дизъюнкция берётся по всем наборам
Пример 1. Составить СДНФ для функции, заданной таблицей:
Поскольку данная таблица (уже встречавшаяся ранее) содержит три единичных набора, СДНФ будет конъюнкцией трёх дизъюнкций. В свою очередь, каждая дизъюнкция включает три переменных – по числу их в функции Получим: Напомним, что, подобно знаку умножения, знак дизъюнкции
Единственная функция, которая не имеет СДНФ – это константа Формулы, содержащие кроме переменных и скобок, только знаки дизъюнкции, конъюнкции и отрицания, будем называть булевыми формулами. Теорема 8.2. Всякая логическая функция может быть представлена булевой функцией, то есть как суперпозиция дизъюнкции, конъюнкции и отрицания.
Выше мы обозначили множество всех логических операций на двухэлементном множестве Определение. Булевой алгеброй логических функций называется алгебра вида Замечание. На практике мы имеем дело не самими функциями, а с представляющими их формулами, то есть с алгеброй формул, которая значительно шире, поскольку каждую функцию представляет бесконечное множество формул. Чтобы “синхронизировать” их алгебре формул придаётся следующий вид. Элементами алгебры формул объявляются не сами формулы, а классы эквивалентности формул, то есть классы формул, представляющих одну и ту же функцию. Определённая таким образом, алгебра формул называется алгеброй Линденбаума - Тарского. Она изоморфна булевой алгебре функций. Теперь рассмотрим основные свойства булевых операций (частично уже знакомые по теме “Элементы математической логики”). 1. Ассоциативность: а) 2. Коммутативность: а) 3. Дистрибутивность конъюнкции относительно дизъюнкции: 4. Дистрибутивность дизъюнкции относительно конъюнкции:
5. Идемпотентность: а) 6. Двойное отрицание: 7. Свойства констант: а) 8. Правила де Моргана: а) 9. Закон противоречия: 10. Закон “исключённого третьего”: Все соотношения 1 – 10 можно проверить указанным ранее стандартным методом – вычислением обеих частей равенств на всех наборах значений переменных. Эти равенства остаются справедливыми и в случае подстановки вместо переменной любой логической функции и, следовательно, любой формулы, представляющей эту функцию. Важно лишь соблюдать следующее правило подстановки формулы вместо переменной. При подстановке формулы Правило подстановки позволяет получать из соотношений 1 – 10 новые эквивалентные соотношения. Заметим, что равенство Замечание. Есть существенная разница между подстановкой и заменой. При подстановке переменная заменяется формулой; при этом формула может быть любой, лишь бы производилась одновременная замена ею всех вхождений переменной. При замене подформул может быть заменена любая подформула, однако, не на любую другую, а только на подформулу, эквивалентную ей. При этом замена всех вхождений исходной подформулы не обязательна.
Пример 2. Возьмём соотношение 8а и подставим вместо переменной
Такие преобразования, использующие эквивалентные соотношения и правило замены, называют эквивалентными преобразованиями. Эквивалентные преобразования являются мощным средством доказательства эквивалентности формул, как правило, более эффективным, чем их вычисление на наборах значений переменных. В булевой алгебре принято опускать скобки в следующих двух случаях: а) при последовательном выполнении нескольких конъюнкций или дизъюнкций; б) если они являются внешними скобками у конъюнкции. Оба соглашения совершенно аналогичны общепринятому опусканию скобок для операции умножения в арифметических выражениях. Рассмотрим несколько способов упрощения формул с помощью эквивалентных преобразований, позволяющих получить формулы, содержащие меньшее количество символов. а) Поглощение: 1)
Далее будем опускать доказательства приводимых равенств, которые при желании можно получить из соотношений 1 – 10 и уже доказанных равенств. б) Склеивание: в) Обобщённое склеивание: г) Одним из главных видов упрощения формул является приведение их к дизъюнктивной нормальной форме (ДНФ). Определение. Элементарными конъюнкциями называются конъюнкции переменных или их отрицаний, в которых каждая переменная встречается не более одного раза. Дизъюнктивной нормальной формой называется формула, имеющая вид дизъюнкции элементарных конъюнкций. Заметим, что СДНФ является частным случаем ДНФ. Приведение формулы к ДНФ выполняется так. Сначала с помощью соотношений 6 и 8 все отрицания “спускаются” до переменных. Затем раскрываются скобки. После этого с помощью соотношений 5, 9 и 10 удаляются лишние конъюнкции и повторения переменных в конъюнкциях. Наконец, с помощью соотношений 7а – 7е удаляются лишние константы. При этом необходимо помнить, что ДНФ данной формулы может быть не единственной. Пример 3. Привести к ДНФ формулу Решение:
Доказано, что если из формулы Теорема 8.3. Для любых двух эквивалентных формул Аналогично понятию ДНФ определяется понятие конъюнктивной нормальной формы (КНФ), то есть КНФ есть конъюнкция элементарных дизъюнкций. Переход от КНФ к ДНФ и обратно всегда осуществим (обычно, с помощью формул Де Моргана). Пример 4. Привести формулу Заменим исходную формулу её двойным отрицанием, а затем применим соотношения 8.
Назад, в начало конспекта.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1289; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.159.212 (0.017 с.) |

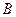 и двоичные переменные, принимающие значения из этого множества. Его элементы часто обозначают 0 и 1, однако они, вообще говоря, не являются числами в обычном смысле (хотя и похожи на них по некоторым свойствам). Наиболее распространённая интерпретация двоичных переменных – логическая: “да” – “нет”, “истинно” – “ложно”. В контексте, содержащем одновременно двоичные и арифметические величины, а также функции, эта интерпретация обычно фиксируется явно. Например, в языках программирования (Pascal и др.) вводится специальный тип переменной – логическая переменная, значения которой обозначаются true и false. В данной лекции логическая интерпретация двоичных переменных не везде является обязательной, поэтому будем считать, что
и двоичные переменные, принимающие значения из этого множества. Его элементы часто обозначают 0 и 1, однако они, вообще говоря, не являются числами в обычном смысле (хотя и похожи на них по некоторым свойствам). Наиболее распространённая интерпретация двоичных переменных – логическая: “да” – “нет”, “истинно” – “ложно”. В контексте, содержащем одновременно двоичные и арифметические величины, а также функции, эта интерпретация обычно фиксируется явно. Например, в языках программирования (Pascal и др.) вводится специальный тип переменной – логическая переменная, значения которой обозначаются true и false. В данной лекции логическая интерпретация двоичных переменных не везде является обязательной, поэтому будем считать, что  , рассматривая 0 и 1 как формальные символы, не имеющие арифметического смысла.
, рассматривая 0 и 1 как формальные символы, не имеющие арифметического смысла. арная операция на множестве
арная операция на множестве 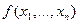 - это функция, принимающая значения 0 или 1. Множество всех логических функций будем обозначать
- это функция, принимающая значения 0 или 1. Множество всех логических функций будем обозначать  , множество всех логических функций
, множество всех логических функций 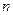 переменных -
переменных -  .
. элементным множеством вместе со всеми операциями на нём, называется алгеброй
элементным множеством вместе со всеми операциями на нём, называется алгеброй  . Мы в дальнейшем будем рассматривать логические функции только из
. Мы в дальнейшем будем рассматривать логические функции только из  .
. ), а в правой части – значение функции на этих наборах значений. Ниже приведена таблица, задающая некоторую функцию трёх переменных.
), а в правой части – значение функции на этих наборах значений. Ниже приведена таблица, задающая некоторую функцию трёх переменных.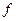 , а множество единичных наборов называют единичным множеством функции
, а множество единичных наборов называют единичным множеством функции 


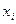 в функции
в функции 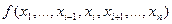 называется несущественной (фиктивной), если
называется несущественной (фиктивной), если 
 при любых значениях остальных переменных.
при любых значениях остальных переменных. переменной, то есть представляет собой некоторую функцию
переменной, то есть представляет собой некоторую функцию 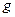 от
от  означает, что при любых значениях
означает, что при любых значениях  выполняется
выполняется  независимо от значения
независимо от значения 
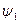



 совпадают со значениями переменной
совпадают со значениями переменной  .
.






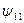

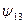
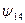

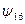
 является конъюнкцией переменных
является конъюнкцией переменных  ,
, 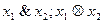 . Её также называют логическим умножением, поскольку таблица её действительно совпадает с таблицей обычного умножения для чисел 0 и 1. Поэтому, кстати, по аналогии с обычным умножением, знак операции между переменными часто опускают:
. Её также называют логическим умножением, поскольку таблица её действительно совпадает с таблицей обычного умножения для чисел 0 и 1. Поэтому, кстати, по аналогии с обычным умножением, знак операции между переменными часто опускают:  .
. будем называть умножением по модулю 2 (см. ниже). Она реализует произведение остатков от деления чисел 0 и 1 на число 2.
будем называть умножением по модулю 2 (см. ниже). Она реализует произведение остатков от деления чисел 0 и 1 на число 2. называется дизъюнкцией переменных
называется дизъюнкцией переменных 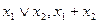 .
. называется неравнозначностью переменных
называется неравнозначностью переменных  .
.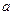 и
и 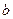 называются сравнимыми по модулю
называются сравнимыми по модулю  , если при делении на это число они дают одинаковые остатки.
, если при делении на это число они дают одинаковые остатки.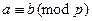 . Например,
. Например,  ,
,  . Так вот, функцию
. Так вот, функцию  называется импликацией или логическим следованием. Обозначается:
называется импликацией или логическим следованием. Обозначается:  .
. называется эквивалентностью или равнозначностью. Она равна 1, если значения переменных одинаковы и 0, если они различны. Обозначается:
называется эквивалентностью или равнозначностью. Она равна 1, если значения переменных одинаковы и 0, если они различны. Обозначается:  .
. называется стрелкой Пирса и обозначается
называется стрелкой Пирса и обозначается  . Функция
. Функция  называется штрихом Шеффера и обозначается
называется штрихом Шеффера и обозначается  . Остальные функции специальных названий не имеют и, как можно показать, легко выражаются через перечисленные выше функции.
. Остальные функции специальных названий не имеют и, как можно показать, легко выражаются через перечисленные выше функции. , а
, а  . Аналогично, в функциях
. Аналогично, в функциях  , а
, а  .
. . Символы переменных
. Символы переменных 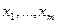 , содержащихся в данных функциях, будем считать формулами глубины 0.
, содержащихся в данных функциях, будем считать формулами глубины 0. имеет глубину
имеет глубину  , если она имеет вид
, если она имеет вид  , где
, где  , а
, а  формулы, максимальная из глубин которых равна
формулы, максимальная из глубин которых равна  . При этом
. При этом  называются подформулами формулы
называются подформулами формулы  называется внешней, или главной операцией формулы
называется внешней, или главной операцией формулы  в наших обозначениях – это формула глубины 1. Выражение
в наших обозначениях – это формула глубины 1. Выражение  является формулой глубины 3, содержащей одну подформулу глубины 2 и две подформулы глубины 1.
является формулой глубины 3, содержащей одну подформулу глубины 2 и две подформулы глубины 1. является конъюнкцией,
является конъюнкцией,  дизъюнкцией, а
дизъюнкцией, а 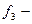 импликацией, то приведённая выше формула примет вид
импликацией, то приведённая выше формула примет вид  .
. , называются формулами над множеством
, называются формулами над множеством  и
и  имеют одну и ту же глубину 3.
имеют одну и ту же глубину 3. к набору
к набору  . Получим:
. Получим:  . Далее получим
. Далее получим  . Наконец,
. Наконец,  .
. из предыдущего пункта (то есть функции И, ИЛИ, НЕ), то функцию
из предыдущего пункта (то есть функции И, ИЛИ, НЕ), то функцию  и
и  . Функцию
. Функцию  и
и  .
. .
. вычислений, если считать, что обе формулы зависят от
вычислений, если считать, что обе формулы зависят от  . Пусть
. Пусть  параметр, равный 0 или 1. Тогда
параметр, равный 0 или 1. Тогда  , если
, если  , и
, и  , если
, если  .
.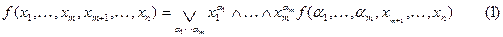 ,
,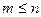 , а дизъюнкция берётся по всем
, а дизъюнкция берётся по всем  наборам значений переменных
наборам значений переменных  .
. и
и  ,
,  разложение (1) имеет вид:
разложение (1) имеет вид:
 .
. , когда разложение производится по всем переменным. При этом все переменные в правой части равенства (1) получают фиксированные значения, и функции в конъюнкциях правой части становятся равными 0 или 1, что даёт:
, когда разложение производится по всем переменным. При этом все переменные в правой части равенства (1) получают фиксированные значения, и функции в конъюнкциях правой части становятся равными 0 или 1, что даёт: ,
, , на которых
, на которых  . Такое разложение называется совершенной дизъюнктивной нормальной формой (СДНФ) функции
. Такое разложение называется совершенной дизъюнктивной нормальной формой (СДНФ) функции  и без отрицания, если
и без отрицания, если 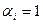 . Таким образом, существует взаимно однозначное соответствие между таблицей функции
. Таким образом, существует взаимно однозначное соответствие между таблицей функции  .
. в логических формулах часто опускают. Тогда полученное выражение примет более компактный вид:
в логических формулах часто опускают. Тогда полученное выражение примет более компактный вид: .
.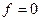 .
. , как
, как  , основным множеством которой является всё множество логических функций, а операциями – дизъюнкция, конъюнкция и отрицание.
, основным множеством которой является всё множество логических функций, а операциями – дизъюнкция, конъюнкция и отрицание. ; б)
; б)  .
. ; б)
; б) 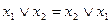 .
. .
. .
.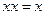 ; б)
; б)  .
. .
. ; б)
; б) 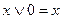 ; в)
; в)  ; г)
; г)  ; д)
; д)  ; е)
; е)  .
. ; б)
; б)  . Очень важные соотношения, которые часто будут использоваться в дальнейшем. С их помощью (а также с помощью соотношения 6) дизъюнкция заменяется конъюнкцией и наоборот.
. Очень важные соотношения, которые часто будут использоваться в дальнейшем. С их помощью (а также с помощью соотношения 6) дизъюнкция заменяется конъюнкцией и наоборот. .
.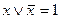 .
. означает в данном контексте, что формулы
означает в данном контексте, что формулы  и
и  описывают одну и ту же логическую функцию. Следовательно, если какая-то формула
описывают одну и ту же логическую функцию. Следовательно, если какая-то формула  . Получим:
. Получим:  . Здесь в обеих частях стоят формулы, неэквивалентные исходным формулам, но эквивалентные между собой. Если же в правой части нового соотношения формулу
. Здесь в обеих частях стоят формулы, неэквивалентные исходным формулам, но эквивалентные между собой. Если же в правой части нового соотношения формулу  заменить формулой
заменить формулой 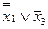 , эквивалентной ей в силу соотношения 8а и затем заменить
, эквивалентной ей в силу соотношения 8а и затем заменить  на
на  . Причём все формулы в полученной цепи преобразований являются эквивалентными:
. Причём все формулы в полученной цепи преобразований являются эквивалентными: .
. и 2)
и 2)  . Докажем данное равенство подробно, используя для доказательства соотношения 3, 7а и 7в.
. Докажем данное равенство подробно, используя для доказательства соотношения 3, 7а и 7в. .
. .
. .
. .
. .
.


 . В итоге получили дизъюнкцию элементарных конъюнкций, то есть ДНФ.
. В итоге получили дизъюнкцию элементарных конъюнкций, то есть ДНФ. к КНФ.
к КНФ.


 .
.


