
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция № 3. Отношения и их свойства.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
1. Основные понятия и определения. Определение. Подмножество Одноместное (одномерное) отношение – это просто некоторое подмножество А. Такие отношения называют признаками. Говорят, что Наиболее часто встречающимися и хорошо изученными являются двухместные или бинарные отношения. Если Пример 1. Бинарные отношения на множестве а) Отношение “ б) Отношение “иметь общий делитель, не равный единице” выполняется для пар в) Отношение “быть делителем” выполняется для пар Пример 2. Бинарные отношения на множестве точек координатной плоскости. а) Отношение “быть равноудалёнными от начала координат” выполнятся для пар точек б) Отношение “принадлежать окружности, центр которой находится в начале координат”, выполняется для первой пары точек из предыдущего примера и не выполняется для второй пары. в) Отношение “быть удалёнными на разное расстояние от начала координат” выполняется для всех точек, для которых не выполняется отношение, описанное в пункте “б”. Пусть дано отношение Строго говоря, само отношение Для задания бинарных отношений можно использовать любые способы задания множеств (например, список пар, для которых данное отношение выполняется). Отношения на конечных множествах обычно задаются списком или матрицей. Матрица бинарного отношения на конечном множестве
Пример 3. Для конечного множества а) б) в)
Поскольку отношения на множестве А задаются подмножествами А2, для отношений можно определить те же операции, что и для множеств. Например, отношение “ Определение. Отношение Непосредственно из определения следует, что
2. Свойства отношений. Определение. Отношение Главная диагональ матрицы рефлексивного отношения содержит только единицы. Определение. Отношение Главная диагональ матрицы рефлексивного отношения содержит только нули. Например, отношения “ Определение. Отношение Матрица симметричного отношения симметрична относительно главной диагонали: Определение. Отношение Отношение “быть симметричным относительно оси абсцисс” является симметричным: если первая точка симметрична второй относительно этой оси, то и вторая точка симметрична первой. Отношение “ Нетрудно убедиться в том, что отношение Определение. Отношение Отношения “быть равным”, “жить в одном городе”, “быть параллельным” являются транзитивными. Отношения “пересекаться”, “быть сыном” не являются транзитивными. Замечание. В отличие от отношений рефлексивности и симметричности, для отношения транзитивности не формулируется противоположного понятия (антитранзитивности). Определение. Транзитивным замыканием Замечание. Замыкание является весьма общим математическим понятием. Упрощённо говоря, замкнутость означает, что многократное повторение допустимых шагов не выводит за определённые границы. Например, множество натуральных чисел замкнуто относительно операции сложения, однако открыто (то есть незамкнуто) относительно операции деления. Если отношение Если отношение Например, транзитивным замыканием отношения “быть сыном” является отношение “быть прямым потомком”, включающее в себя понятия “быть сыном”, “быть внуком”, “быть правнуком” и так далее.
Назад, в начало конспекта.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1025; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.007 с.) |

 называется
называется  местным (
местным ( находятся в отношении
находятся в отношении  , если
, если  .
.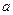 обладает признаком
обладает признаком  и
и  . Свойства одноместных отношений – это свойства подмножеств А, поэтому для случая
. Свойства одноместных отношений – это свойства подмножеств А, поэтому для случая  термин “отношения” употребляется редко.
термин “отношения” употребляется редко.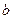 находятся в отношении
находятся в отношении  .
.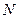 .
. ” выполняется для пар
” выполняется для пар  и не выполняется для пары
и не выполняется для пары  .
. и не выполняется для пар
и не выполняется для пар  .
. и не выполняется для пар
и не выполняется для пар  .
. и
и 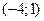 , но не выполнятся для пары точек
, но не выполнятся для пары точек  и
и 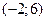 .
.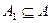 определяется отношение
определяется отношение 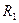 , называемое сужением
, называемое сужением  , которое получается из отношения
, которое получается из отношения  .
. - это квадратная матрица
- это квадратная матрица  порядка
порядка 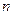 , в которой каждый элемент
, в которой каждый элемент  определяется следующим образом:
определяется следующим образом: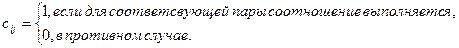
 матрицы отношений из примера 1 (а – в) приведены в следующих таблицах.
матрицы отношений из примера 1 (а – в) приведены в следующих таблицах. называется обратным к отношению
называется обратным к отношению  тогда и только тогда, когда
тогда и только тогда, когда  . Например, для отношения “
. Например, для отношения “  ”.
”. имеет место
имеет место  .
. ” и “иметь сына” являются антирефлексивными. Отношение “быть симметричным относительно оси абсцисс” не является ни рефлексивным, ни антирефлексивным: точка плоскости симметрична сама себе, если лежит на этой оси, и не симметрична себе, если не лежит на ней.
” и “иметь сына” являются антирефлексивными. Отношение “быть симметричным относительно оси абсцисс” не является ни рефлексивным, ни антирефлексивным: точка плоскости симметрична сама себе, если лежит на этой оси, и не симметрична себе, если не лежит на ней. из отношения
из отношения  . Иными словами, отношение
. Иными словами, отношение  для любых
для любых  .
. .
.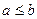 и
и 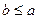 , это означает, что
, это означает, что  .
. из отношений
из отношений  следует
следует  .
.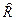 отношения
отношения  существует цепочка из
существует цепочка из  , в которой между каждыми двумя соседними элементами выполняется отношение
, в которой между каждыми двумя соседними элементами выполняется отношение  , то говорят, что существует транзитивное замыкание
, то говорят, что существует транзитивное замыкание  .
. (и наоборот). Например, отношение “быть делителем” транзитивно для любой цепочки элементов и само является транзитивным замыканием этого отношения.
(и наоборот). Например, отношение “быть делителем” транзитивно для любой цепочки элементов и само является транзитивным замыканием этого отношения. .
.


