
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция № 11. Полнота и замкнутость.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Ранее нами рассматривались два способа задания логических функций – табличный и с помощью формул. Таблица задаёт функцию непосредственно как соответствие между двоичными наборами и значениями функции на этих наборах. Этот способ универсален, то есть, пригоден для любых функций, однако слишком громоздок. Формула – гораздо более компактный способ задания функции, но она задаёт функцию через другие функции. Поэтому для любой системы функций
Определение. Система функций Из теоремы 8.2 следует, что система Теорема 11.1. Если все функции функционально полной системы Пример 1. а) Системы
С точки зрения функциональной полноты систему б) Системы
Таким образом, система в) Система На свойствах этой системы остановимся подробнее.
Определение. Алгебра над множеством логических функций с двумя бинарными операциями Замечание. Операция В алгебре Жегалкина выполняются следующие соотношения (знак умножения 2.1. 2.2. 2.3 2.4 Кроме того, выполняются соотношения, ранее сформулированные булевой алгебры, относящиеся к конъюнкции и константам. Отрицание и дизъюнкция выражаются так: 2.5 2.6 Если в произвольной формуле алгебры Жегалкина раскрыть скобки и произвести все упрощения по вышеуказанным соотношениям, то получится формула, имеющая вид Суммы произведений, то есть полином (многочлен) по модулю 2. Такая формула называется полиномом Жегалкина для данной функции. От булевой формулы всегда можно перейти к формуле алгебры Жегалкина, используя равенства 2.5 и 2.6, а также прямое следствие из равенства 2.6: если Пример 2. Составить полиномы Жегалкина для данных функций: а) б) Заметим, что если в полученных полиномах Жегалкина произвести обратную замену функций, то получим упрощённые формулы булевой алгебры. Теорема 11.2. Для всякой логической функции существует полином Жегалкина и притом единственный. Существование такого полинома, по сути, уже доказано, а для доказательства его единственности достаточно показать существование взаимно однозначного соответствия между множеством всех функций Определение. Функция, у которой полином Жегалкина имеет вид Все функции от одной переменной линейны. Также линейными являются функции эквивалентность и сумма по модулю 2.
Определение. Множество Всякая система Пример 3. а) Множество всех дизъюнкций, то есть функций вида б) Множество всех линейных функций является замкнутым классом, так как подстановка формул вида Важнейшим примером замкнутого класса является класс монотонных функций, который будет рассмотрен далее. Ранее рассматривалось отношение частичного порядка Определение. Функция Пример 4. а) Функция б) Дизъюнкция и конъюнкция любого числа переменных являются монотонными функциями. в) Рассмотрим две функции от трёх переменных, заданных следующей таблицей.
Функция Проверка монотонности функции непосредственно по определению требует анализа таблицы функции и может оказаться достаточно трудоёмкой. Поэтому весьма полезной для установления монотонности является следующая теорема. Всякая булева формула, не содержащая отрицаний, представляет собой монотонную функцию отличную от константы; наоборот, для любой монотонной функции, отличной от 0 и 1, найдётся представляющая её булева формула без отрицаний. Теорема 11.3. Всякая булева формула, не содержащая отрицаний, представляет собой монотонную функцию отличную от константы; наоборот, для любой монотонной функции, отличной от 0 и 1, найдётся представляющая её булева формула без отрицаний. Из данной теоремы и того очевидного факта, что подстановка нескольких формул без отрицаний в формулу без отрицаний снова даёт формулу без отрицаний, вытекает следующая теорема. Теорема 11.4. Множество всех монотонных функций является замкнутым классом. Но поскольку всякая булева формула без отрицаний является суперпозицией дизъюнкций и конъюнкций, из данной теоремы непосредственно получаем следствие. Следствие. Класс монотонных функций является замыканием системы функций
Теперь перейдём к рассмотрению основного вопроса, поставленного в рамках данной лекции: каковы необходимые и достаточные условия функциональной полноты для произвольной системы функций Лемма 1 (о немонотонных функциях). Если функция Практически данная лемма является утверждением, противоположным теореме, обратной к теореме 11.3. Смысл её заключается в том, что для функции Лемма 2 (о нелинейных функциях). Если функция Иначе говоря, существует представление дизъюнкции и конъюнкции в виде суперпозиции констант, отрицаний и нелинейной функции Замечание. При традиционных обозначениях переменных в выражениях вида Две указанные леммы позволяют получить все булевы операции с помощью немонотонных функций, нелинейных функций и констант. Это ещё не полнота в точном смысле слова, так как константы с самого начала предполагались данными. Однако такое предположение часто бывает оправданным в различных приложениях (прежде всего в синтезе логических схем). Поэтому есть смысл ввести ослабленное определение полноты. Определение. Система функций Очевидно, что из обычной полноты системы следует её слабая полнота. Теорема 11.5 (первая теорема о функциональной полноте). Для того, чтобы система функций Доказательство: 1) Необходимость. Классы монотонных и линейных функций замкнуты и содержат 0 и 1. Поэтому если 2) Достаточность. Пусть Пример 5. а) Система б) В функционально полной системе Для формулировки необходимых и достаточных условий “cильной” полноты (в отличие от слабой) нужно ввести ряд определений, описывающих ещё три замкнутых класса функций. Определение. Функция Оба данных класса функций являются замкнутыми, что проверяется подстановкой констант в суперпозиции. Равным образом замкнутый класс образуют самодвойственные функции (такие, что Теорема 11.6 (вторая – основная – теорема о функциональной полноте). Для того чтобы система функций Назад, в начало конспекта.
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1658; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.008 с.) |

 возникает естественный вопрос: всякая ли логическая функция представима формулой в этой системе. В позапрошлой лекции был получен положительный ответ для системы
возникает естественный вопрос: всякая ли логическая функция представима формулой в этой системе. В позапрошлой лекции был получен положительный ответ для системы  (теорема 8.2). В данной лекции будет показано, как решать этот вопрос для произвольной системы
(теорема 8.2). В данной лекции будет показано, как решать этот вопрос для произвольной системы 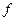 из такой системы следует составить булеву формулу (а она обязательно существует согласно теореме 8.2) и потом выразить в ней конъюнкцию, дизъюнкцию и отрицание через функции системы
из такой системы следует составить булеву формулу (а она обязательно существует согласно теореме 8.2) и потом выразить в ней конъюнкцию, дизъюнкцию и отрицание через функции системы 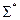 представимы формулами над системой
представимы формулами над системой  и
и  функционально полны. Действительно, с помощью законов Де Моргана и двойного отрицания можно выразить в каждой из этих систем функцию, недостающую до
функционально полны. Действительно, с помощью законов Де Моргана и двойного отрицания можно выразить в каждой из этих систем функцию, недостающую до 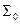 через остальные две:
через остальные две: .
. и
и  не являются избыточными, зато формулы в них получаются гораздо длиннее: замена одной операции на другую вносит в формулу сразу три лишних отрицания.
не являются избыточными, зато формулы в них получаются гораздо длиннее: замена одной операции на другую вносит в формулу сразу три лишних отрицания. (штрих Шеффера) и
(штрих Шеффера) и  (стрелка Пирса) являются функционально полными.
(стрелка Пирса) являются функционально полными. .
. сводится к системе
сводится к системе 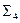 - к системе
- к системе  (
(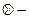 умножение по модулю 2,
умножение по модулю 2,  сложение по модулю 2 – см. пункт 1 лекции № 8)) является функционально полной. Поскольку
сложение по модулю 2 – см. пункт 1 лекции № 8)) является функционально полной. Поскольку  , данная система сводится к
, данная система сводится к 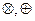 называется алгеброй Жегалкина.
называется алгеброй Жегалкина. вполне аналогична операции конъюнкции (логического умножения). Однако операция
вполне аналогична операции конъюнкции (логического умножения). Однако операция  имеет совершенно другой математический смысл, чем дизъюнкция (соответствующая функция ранее была названа неравнозначностью). Поэтому никак нельзя считать алгебру Жегалкина иной формой записи булевой алгебры.
имеет совершенно другой математический смысл, чем дизъюнкция (соответствующая функция ранее была названа неравнозначностью). Поэтому никак нельзя считать алгебру Жегалкина иной формой записи булевой алгебры. ,
,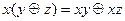 ,
, ,
,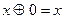 .
. .
. , то
, то  . Оно, в частности, позволяет заменять знак дизъюнкции знаком
. Оно, в частности, позволяет заменять знак дизъюнкции знаком  ,
, .
.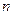 переменных и множеством всех полиномов Жегалкина.
переменных и множеством всех полиномов Жегалкина. , где параметры
, где параметры  равны нулю или единице, называется линейной.
равны нулю или единице, называется линейной. логических функций называется замкнутым классом, если любая суперпозиция функций из множества
логических функций называется замкнутым классом, если любая суперпозиция функций из множества  . Если множество
. Если множество 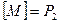 .
. является замкнутым классом.
является замкнутым классом. на множестве векторов одинаковой длины. Напомним, что для векторов
на множестве векторов одинаковой длины. Напомним, что для векторов  и
и  выполняется
выполняется 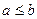 , если для любого
, если для любого  выполняется
выполняется 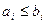 . Здесь воспользуемся этим отношением для двоичных векторов.
. Здесь воспользуемся этим отношением для двоичных векторов. называется монотонной, если для любых двух двоичных наборов длины
называется монотонной, если для любых двух двоичных наборов длины  .
. монотонна.
монотонна.




 , а
, а  . Монотонность функции
. Монотонность функции  .
. константы, что функция оставшейся одной переменной является отрицанием.
константы, что функция оставшейся одной переменной является отрицанием.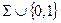 , то есть является суперпозицией констант и функций из системы
, то есть является суперпозицией констант и функций из системы  функционально полна в слабом смысле, так как операция
функционально полна в слабом смысле, так как операция  ) немонотонна.
) немонотонна. единственная функция – штрих Шеффера – нелинейна и немонотонна.
единственная функция – штрих Шеффера – нелинейна и немонотонна. и сохраняющей единицу, если выполняется
и сохраняющей единицу, если выполняется 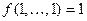 .
.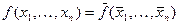 ).
).


