Сходимость и полнота в метрических пространствах
Определение 1. Последовательность точек  эвклидова пространства сходится по метрике эвклидова пространства сходится по метрике  к точке к точке  , если числовая последовательность , если числовая последовательность  , то есть , то есть 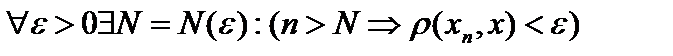 . .
Обозначение используется обычное:  . Таким образом, в метрических пространствах полностью используется вся теория числовых последовательностей. Например: . Таким образом, в метрических пространствах полностью используется вся теория числовых последовательностей. Например:
Теорема 1. Последовательность точек метрического пространства может иметь только один предел.
  . Пусть последовательность . Пусть последовательность  имеет два предела, то есть имеет два предела, то есть  и и  . Тогда в неравенстве треугольника для точек . Тогда в неравенстве треугольника для точек  и и  где где  , , 
правая часть стремится к нулю, а левая часть постоянна и отлична от нуля. 
Определение 2. Сходимость по норме (метрике) пространства  называется равномерной сходимостью.Сходимость по (метрике) норме пространства называется равномерной сходимостью.Сходимость по (метрике) норме пространства  называется сходимостью в среднем. называется сходимостью в среднем.
Определение 3. Последовательность точек x1, x2, x3,... пространства (Х, r) называется фундаментальной,если для любого числа e>0 найдется такое число n0, что для всех n, m > n0 выполняется неравенство r(xm, xn)<e.
Всякая сходящаяся последовательность является фундаментальной.
Определение 4. Метрическое пространство, в котором всякая фундаментальная последовательность сходится, называется полным.
Комментарий. Все стандартные метрические пространства, кроме  , полны, а так как они ещё и нормированы, то все стандартные метрические пространства, кроме , полны, а так как они ещё и нормированы, то все стандартные метрические пространства, кроме  , являются банаховыми. , являются банаховыми.
Пример1. Покажем полноту пространства  . .  То, что это метрическое пространство, следует из того, что То, что это метрическое пространство, следует из того, что  . Пусть по метрике пространства . Пусть по метрике пространства  последовательность последовательность  , то есть , то есть  . Но тогда это выполняется и для всех других . Но тогда это выполняется и для всех других  , то есть , то есть  равномерно (номер равномерно (номер  обеспечивает сходимость обеспечивает сходимость  для всех для всех  сразу. Но тогда по теореме Вейерштрасса предел равномерно сходящейся последовательности непрерывных функций есть функция непрерывная, то есть функция сразу. Но тогда по теореме Вейерштрасса предел равномерно сходящейся последовательности непрерывных функций есть функция непрерывная, то есть функция  непрерывна, то есть непрерывна, то есть  и пространство и пространство  полно. полно. 
Теорема 2. Всякое замкнутое подпространство  полного метрического пространства полного метрического пространства  является полным пространством. является полным пространством.
 Пусть последовательность точек Пусть последовательность точек  фундаментальна в пространстве фундаментальна в пространстве  . Тогда она будет фундаментальной и в пространстве . Тогда она будет фундаментальной и в пространстве  . А поскольку оно полное, то эта последовательность сходится, . А поскольку оно полное, то эта последовательность сходится,  . Поскольку множество . Поскольку множество  замкнуто, то точка замкнуто, то точка  предельная для множества предельная для множества  , что и доказывает полноту пространства , что и доказывает полноту пространства  . .  . .
Комментарий. Тот факт, что в полных пространствах понятия замкнутости и полноты для подпространств совпадают, очень важен в приложениях. Однако, надо следить за полнотой исходного пространства.
Пример 2. Рассмотрим множество  . Оно, очевидно, не замкнуто и не полно. Пусть . Оно, очевидно, не замкнуто и не полно. Пусть  . Это множество не замкнуто, хотя состоит из бесконечного числа замкнутых множеств, так как не любая последовательность из этого множества сходится к пределу, ему принадлежащему. Но оно не полно, так как предел этой последовательности равен нулю, которого нет в множестве . Это множество не замкнуто, хотя состоит из бесконечного числа замкнутых множеств, так как не любая последовательность из этого множества сходится к пределу, ему принадлежащему. Но оно не полно, так как предел этой последовательности равен нулю, которого нет в множестве  . .
Пример 3. Покажем неполноту пространства  при при  . .  Это метрическое пространство, так как Это метрическое пространство, так как  , покажем, что , покажем, что  . .  Пусть при каком-то Пусть при каком-то   . Тогда в силу непрерывности эта ситуация должна сохраниться и в . Тогда в силу непрерывности эта ситуация должна сохраниться и в  окрестности точки окрестности точки  , то есть , то есть  . .  Проверим третью аксиому: Проверим третью аксиому: 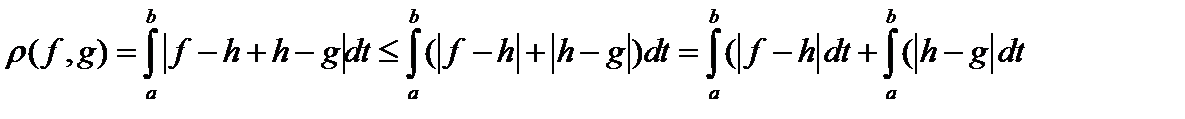 . .
Проверим полноту. Пусть последовательность  , то есть , то есть 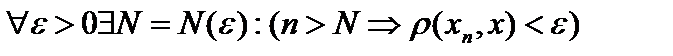 , ,  , где , где  . Выберем . Выберем  тогда тогда  . На участке вне . На участке вне  функции совпадают и равны единице, то есть функции совпадают и равны единице, то есть  и, таким образом, последовательность и, таким образом, последовательность  фундаментальна. Ясно, что её пределом будет функция фундаментальна. Ясно, что её пределом будет функция  В самом деле, В самом деле,  , то есть последовательность , то есть последовательность  , но функция , но функция  разрывна, разрывна,  . Это и означает неполноту пространства . Это и означает неполноту пространства  . . 

Комментарий. Можно ли пополнить данное метрическое пространство или, более широко, можно ли пополнить любое метрическое пространство? Принципиальный ответ  да. Но для этого иногда нужно идти на коренной пересмотр ситуации. В частности, пространство функций, интегрируемых по Риману, пополнить невозможно, поэтому для того, чтобы сделать пространство да. Но для этого иногда нужно идти на коренной пересмотр ситуации. В частности, пространство функций, интегрируемых по Риману, пополнить невозможно, поэтому для того, чтобы сделать пространство  полным, надо менять процедуру интегрирования. Позже мы построим интеграл Лебега и убедимся, что пространство функций, интегрируемых по Лебегу и, следовательно, и пространство полным, надо менять процедуру интегрирования. Позже мы построим интеграл Лебега и убедимся, что пространство функций, интегрируемых по Лебегу и, следовательно, и пространство  уже полно. уже полно.
Примеры. 1. Верно ли, что последовательность  , если , если  в в 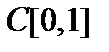 и и  ? ?  В пространстве В пространстве 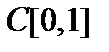  . В пространстве . В пространстве   . Тогда . Тогда  . .
2. Верно ли, что последовательность  , если , если 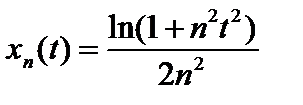 в пространстве в пространстве  ? ?
   . . 
3. Показать полноту дискретного метрического пространства.
 В дискретном метрическом пространстве все точки изолированные, поэтому фундаментальной последовательностью может быть только стационарная, которая всегда сходится. В дискретном метрическом пространстве все точки изолированные, поэтому фундаментальной последовательностью может быть только стационарная, которая всегда сходится. 
4. Найти предел последовательности  в пространстве C [0,2], если он существует. в пространстве C [0,2], если он существует.
 Необходимым условием сходимости последовательности в пространстве C [ a,b ] является существование предела xn при каждом фиксированном Необходимым условием сходимости последовательности в пространстве C [ a,b ] является существование предела xn при каждом фиксированном 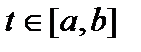 . Заданная последовательность при заданном t сходится к функции a(t)=t. Данная функция непрерывна. . Заданная последовательность при заданном t сходится к функции a(t)=t. Данная функция непрерывна.
Проверим, сходится ли последовательность xn к функции a(t) по норме пространства C [ a,b ], т.е. равномерно. Вычислим  . По определению нормы: . По определению нормы: 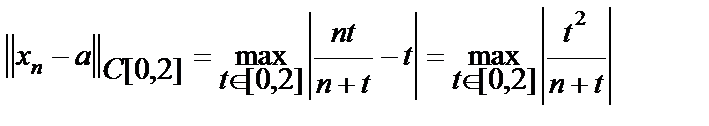 . Вычислим максимум функции . Вычислим максимум функции  на отрезке [0,2]. Для этого вычислим критические точки. на отрезке [0,2]. Для этого вычислим критические точки.  Таким образом, точками, подозрительными на экстремум, являются точки Таким образом, точками, подозрительными на экстремум, являются точки  . Поскольку . Поскольку 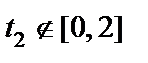 , поэтому остается лишь точка , поэтому остается лишь точка  . Вычислим также значение функции на концах отрезка: . Вычислим также значение функции на концах отрезка:
 . То есть . То есть  . Это означает, что последовательность . Это означает, что последовательность  в пространстве C [0,2] сходится к функции a(t)=t. в пространстве C [0,2] сходится к функции a(t)=t. 
5. Найти предел последовательности  в пространстве C [0,1], если он существует. в пространстве C [0,1], если он существует.
 Последовательность Последовательность  . Вычислим . Вычислим  . Так как . Так как  , то , то  , если , если  . Точкой, подозрительной на экстремум, является и точка . Точкой, подозрительной на экстремум, является и точка  . Непосредственной проверкой убеждаемся, что максимум достигается в точке . Непосредственной проверкой убеждаемся, что максимум достигается в точке  . Поэтому . Поэтому  . Значит, последовательность . Значит, последовательность  в пространстве C [0,1] не сходится. в пространстве C [0,1] не сходится. 
6. Сходится ли последовательность  в пространстве в пространстве  ? ?
 Необходимым условием сходимости последовательности в пространстве Необходимым условием сходимости последовательности в пространстве  является наличие покоординатного предела. Выпишем несколько членов последовательности: является наличие покоординатного предела. Выпишем несколько членов последовательности:  . Ясно, что последовательность . Ясно, что последовательность  покоординатно сходится к точке покоординатно сходится к точке  . Заметим, что . Заметим, что  , т.к. , т.к.  . Покажем, что последовательность . Покажем, что последовательность  сходится к точке a по норме пространства сходится к точке a по норме пространства  : :
 при при  . .
Следовательно,  . . 
7. Сходится ли последовательность  в пространстве в пространстве  . .
 Очевидно, что точка Очевидно, что точка  является покоординатным пределом последовательности, но является покоординатным пределом последовательности, но  , т.к. ряд, составленный из единиц, не является сходящимся. Следовательно, последовательность , т.к. ряд, составленный из единиц, не является сходящимся. Следовательно, последовательность  не имеет предела. не имеет предела. 
8. Доказать, что последовательность  сходится поточечно к функции сходится поточечно к функции  для всех для всех  , но не сходится в пространстве , но не сходится в пространстве  . .
 Последовательность Последовательность  при каждом фиксированном при каждом фиксированном  стремится к нулю, так как стремится к нулю, так как  . Вычислим . Вычислим
 . Значит, последовательность . Значит, последовательность  не сходится в пространстве не сходится в пространстве  . . 
9. Показать, что пространство 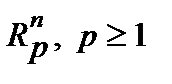 , полное. , полное.  Пусть Пусть  фундаментальная последовательность в фундаментальная последовательность в  . Тогда . Тогда  . Отсюда следует покоординатная сходимость . Отсюда следует покоординатная сходимость  и, следовательно, фундаментальность числовых последовательностей и, следовательно, фундаментальность числовых последовательностей  . Но пространство действительных чисел полное и последовательности . Но пространство действительных чисел полное и последовательности  сходятся. Следовательно, сходится и последовательность сходятся. Следовательно, сходится и последовательность  . . 
10. Показать полноту пространства  . .
11. Дана последовательность
 . .
К какой последовательности она сходится покоординатно? Сходится ли она к тому же пределу в метриках пространств  ? ?  Ясно, что покоординатно последовательность Ясно, что покоординатно последовательность  сходится к нулю. сходится к нулю.



Комментарий. Из предыдущего примера не следует, что всегда из покоординатной сходимости следует сходимость по метрике соответствующего пространства.
12. Дана последовательность
 . Ясно, что покоординатно последовательность . Ясно, что покоординатно последовательность  сходится к нулю. Однако в пространстве сходится к нулю. Однако в пространстве 
13. Множество всех многочленов в пространстве  не является замкнутым, так как, например, функцию не является замкнутым, так как, например, функцию  можно приблизить частичными суммами ряда Тейлора, которые являются алгебраическими многочленами. Следовательно, множество всех многочленов в пространстве не содержит всех предельных точек, и, значит, оно не является замкнутым. можно приблизить частичными суммами ряда Тейлора, которые являются алгебраическими многочленами. Следовательно, множество всех многочленов в пространстве не содержит всех предельных точек, и, значит, оно не является замкнутым.
Сравнение метрик (норм)
Определение 1. Метрика (норма) ρ1 сильнее, чем метрика (норма) ρ2, если из сходимости последовательности  по ρ1 следует её сходимость по ρ2, но существует по ρ1 следует её сходимость по ρ2, но существует  хоть одна последовательность, которая сходится по норме ρ2, но не сходится по норме ρ1. хоть одна последовательность, которая сходится по норме ρ2, но не сходится по норме ρ1.
Определение 2. Две метрики (нормы) ρ1 и ρ2 эквивалентны, если из сходимости последовательности  по ρ1 следует её сходимость по ρ2 и наоборот. по ρ1 следует её сходимость по ρ2 и наоборот.
Определение 2*. Две метрики (нормы) ρ1 и ρ2 эквивалентны, если существуют  или или  . .
Теорема 1. В любых конечномерных пространствах все метрики (нормы) эквивалентны.
 Рассмотрим нормированное пространство Рассмотрим нормированное пространство  , ,  , система векторов , система векторов  образует базис в нём, то есть образует базис в нём, то есть
 . Эвклидова норма . Эвклидова норма  , а , а   ещё одна норма в этом пространстве. Оценим её. ещё одна норма в этом пространстве. Оценим её.  . Обозначив . Обозначив  , получим , получим  . Покажем, что . Покажем, что  в свою очередь подчинена в свою очередь подчинена 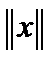 . Рассмотрим функцию . Рассмотрим функцию  переменных переменных  на сфере на сфере 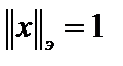 . Она непрерывна, так как . Она непрерывна, так как  и стремится к нулю при и стремится к нулю при  . Единичная сфера . Единичная сфера   замкнутое ограниченное множество, поэтому на ней, в соответствии с теоремой Вейерштрасса, функция достигает своих точных верхней и нижней граней. То есть на сфере замкнутое ограниченное множество, поэтому на ней, в соответствии с теоремой Вейерштрасса, функция достигает своих точных верхней и нижней граней. То есть на сфере  имеем имеем  . . 
Пример. Доказать, что метрика  пространства пространства  сильнее метрики сильнее метрики  пространства пространства 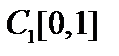 . .
  , то есть , то есть  не слабее не слабее  . Теперь укажем последовательность . Теперь укажем последовательность  , которая сходится по , которая сходится по  , но не сходится по , но не сходится по  . Эта последовательность . Эта последовательность  стандартный пробник функционального анализа, стандартный пробник функционального анализа,  . . 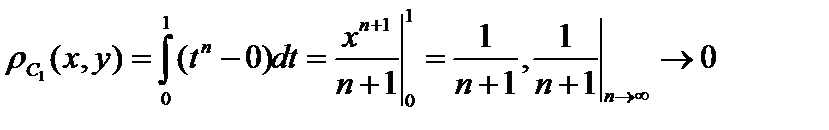 , а , а  , то есть эта последовательность сходится по , то есть эта последовательность сходится по  , но не сходится по , но не сходится по  . . 
Комментарий. В линейной алгебре показывалось, что все линейные структуры изоморфны, то есть существует возможность установить биекцию между ними. Эта теорема утверждает большее  отображение между метрическими пространствами не только взаимно однозначно, но и взаимно непрерывно, то есть гомеоморфно. В конечномерных пространствах все метрики (нормы)топологически эквивалентныв следующем смысле: для шара отображение между метрическими пространствами не только взаимно однозначно, но и взаимно непрерывно, то есть гомеоморфно. В конечномерных пространствах все метрики (нормы)топологически эквивалентныв следующем смысле: для шара  радиуса R с центром в точке радиуса R с центром в точке  , построенного на основе одной из норм, можно построить вписанный в него и описанный вокруг него шары, построенные на основе другой нормы (разумеется, другого радиуса). В бесконечномерных пространствах это не так. , построенного на основе одной из норм, можно построить вписанный в него и описанный вокруг него шары, построенные на основе другой нормы (разумеется, другого радиуса). В бесконечномерных пространствах это не так.
Пример. Покажем, что чебышевская норма, по крайней мере, не слабее гёльдеровской, а дифференциальная не слабее чебышёвской.  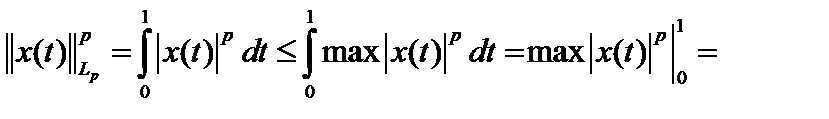  , но , но 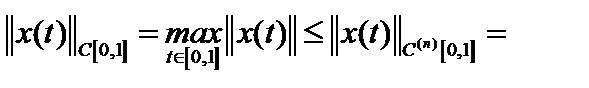
  . . 
Плотность и сепарабельность
Определение 1. Множество M называется плотным в множестве 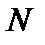 , если , если  , то есть любой элемент из множества , то есть любой элемент из множества 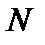 есть предельная точка множества M. (Определение предельной точки и замыкания даны в п.2.3.4.) есть предельная точка множества M. (Определение предельной точки и замыкания даны в п.2.3.4.)
Определение 2. Если множество  , то есть совпадает со всем носителем метрического пространства , то есть совпадает со всем носителем метрического пространства  , то множество M называется всюду плотным (абсолютно плотным) в множестве , то множество M называется всюду плотным (абсолютно плотным) в множестве  . .
Комментарий. Абсолютная плотность означает, что любой элемент из множества  есть предел последовательности элементов из множества M, то есть есть предел последовательности элементов из множества M, то есть  в любой, сколь угодно малой окрестности точки в любой, сколь угодно малой окрестности точки  найдутся точки из множества M, то есть все точки найдутся точки из множества M, то есть все точки  есть точки прикосновения множества M, то есть замыкание множества M совпадает со всем пространством. есть точки прикосновения множества M, то есть замыкание множества M совпадает со всем пространством.
Определение 3. Множество M называется нигде не плотным в множестве  , если , если    шар, не содержащий точек из множества M. шар, не содержащий точек из множества M.
Примеры.  Множество рациональных чисел всюду плотно на действительной оси. Множество рациональных чисел всюду плотно на действительной оси.
 Множество целых чисел нигде не плотно на действительной оси. Множество целых чисел нигде не плотно на действительной оси.
 Любое дискретное множество нигде не плотно в пространстве. Любое дискретное множество нигде не плотно в пространстве.
 Любая изолированная точка есть нигде не плотное множество. Любая изолированная точка есть нигде не плотное множество.
 Любое подмножество нигде не плотного множества нигде не плотно. Любое подмножество нигде не плотного множества нигде не плотно.
 Объединение конечного числа нигде не плотных множеств нигде не плотно. Объединение конечного числа нигде не плотных множеств нигде не плотно.
 Объединение счётного числа нигде не плотных множеств уже не нигде не плотно. Оно может быть даже всюду плотно. Множество рациональных чисел Объединение счётного числа нигде не плотных множеств уже не нигде не плотно. Оно может быть даже всюду плотно. Множество рациональных чисел  счётное всюду плотное множество на действительной оси, но оно есть объединение счётного числа изолированных точек. счётное всюду плотное множество на действительной оси, но оно есть объединение счётного числа изолированных точек.
Определение 4. Метрическое пространство  сепарабельно, если в нём существует счётное всюду плотное множество сепарабельно, если в нём существует счётное всюду плотное множество   счётный скелет. счётный скелет.
Комментарий. Сепарабельность означает, что в пространстве  существует последовательность существует последовательность  , такая, что , такая, что  из неё можно выделить (separate (лат) из неё можно выделить (separate (лат)  выделять) подпоследовательность выделять) подпоследовательность  , сходящуюся к , сходящуюся к  , или, что тоже самое, , или, что тоже самое,  . .
Примеры.  Эвклидово пространство Эвклидово пространство  сепарабельно. Счётный скелет в нём сепарабельно. Счётный скелет в нём  множество точек с рациональными координатами. множество точек с рациональными координатами.
 Дискретное метрическое пространство, состоящее из счётного числа точек, сепарабельно. Дискретное метрическое пространство, состоящее из счётного числа точек, сепарабельно.  По определению,множество называется всюду плотным, если его замыкание совпадает со всем пространством. Здесь счётный скелет совпадает со всем пространством, а других точек нет. По определению,множество называется всюду плотным, если его замыкание совпадает со всем пространством. Здесь счётный скелет совпадает со всем пространством, а других точек нет. 
 Пространство Пространство  сепарабельно. сепарабельно.  Счётный скелет здесь образует множество полиномов с рациональными коэффициентами Счётный скелет здесь образует множество полиномов с рациональными коэффициентами  по теореме Вейерштрасса любую функцию из по теореме Вейерштрасса любую функцию из  можно сколь угодно точно представить в виде суммы таких полиномов. можно сколь угодно точно представить в виде суммы таких полиномов. 
 Пространство Пространство  сепарабельно. сепарабельно.  Рассмотрим множество Рассмотрим множество  всех последовательностей с рациональными членами, у которых только конечное, для каждого своё, число членов не равно нулю, а остальные члены нулевые. Это счётное множество, как объединение счётного числа счётных множеств. Покажем, что множество всех последовательностей с рациональными членами, у которых только конечное, для каждого своё, число членов не равно нулю, а остальные члены нулевые. Это счётное множество, как объединение счётного числа счётных множеств. Покажем, что множество  образует счётный скелет в образует счётный скелет в  . Пусть последовательность . Пусть последовательность  . Так как . Так как  , то есть ряд сходится, то , то есть ряд сходится, то 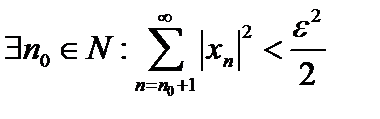 . Так как множество рациональных чисел . Так как множество рациональных чисел  всюду плотно на числовой оси, то. Нормировочный множитель выбран для удобства и в си всюду плотно на числовой оси, то. Нормировочный множитель выбран для удобства и в си  лу произвольности лу произвольности  . Рассмотрим последовательность . Рассмотрим последовательность  , члены которой при , члены которой при  равны нулю. Тогда расстояние между равны нулю. Тогда расстояние между  и и   , то есть , то есть  , то есть замыкание , то есть замыкание  совпадает с совпадает с  , то есть множество , то есть множество  образует счётный скелет в образует счётный скелет в  . . 
 Пространство Пространство  ( (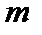 ) не сепарабельно. ) не сепарабельно.  Пусть Пусть  . Тогда . Тогда   двоичное представление числа, а множество всех таких чисел имеет мощность континуума. В метрике двоичное представление числа, а множество всех таких чисел имеет мощность континуума. В метрике   . Пусть пространство . Пусть пространство  сепарабельно, то есть в нём существует счётное всюду плотное множество сепарабельно, то есть в нём существует счётное всюду плотное множество   счётный скелет. Опишем вокруг каждого элемента из счётный скелет. Опишем вокруг каждого элемента из  шар шар  . Всего элементов . Всего элементов  счётное множество, то есть и шаров счётное множество, то есть и шаров  счётное множество, а множество элементов в пространстве счётное множество, а множество элементов в пространстве  имеет мощность континуума, то есть по крайней мере в одном из шаров должно находиться по крайней мере два элемента из пространства имеет мощность континуума, то есть по крайней мере в одном из шаров должно находиться по крайней мере два элемента из пространства  (принцип Вейерштрасса). Пусть (принцип Вейерштрасса). Пусть   центр такого шара. Тогда центр такого шара. Тогда  . . 
Теорема 1. Во всяком сепарабельном предгильбертовом пространстве  существует ортонормированный базис из конечного или счётного числа элементов. существует ортонормированный базис из конечного или счётного числа элементов.
 Пусть Пусть  счётный скелет пространства счётный скелет пространства  . Выбросив из него элементы, которые можно представить в виде линейной комбинации оставшихся элементов, получим полную линейно независимую систему функций, ортонормируя которую и получим базис. . Выбросив из него элементы, которые можно представить в виде линейной комбинации оставшихся элементов, получим полную линейно независимую систему функций, ортонормируя которую и получим базис. 
|



 эвклидова пространства сходится по метрике
эвклидова пространства сходится по метрике  к точке
к точке  , если числовая последовательность
, если числовая последовательность  , то есть
, то есть 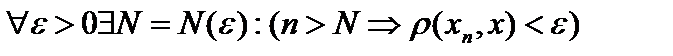 .
. . Таким образом, в метрических пространствах полностью используется вся теория числовых последовательностей. Например:
. Таким образом, в метрических пространствах полностью используется вся теория числовых последовательностей. Например:
 . Пусть последовательность
. Пусть последовательность  имеет два предела, то есть
имеет два предела, то есть  и
и  . Тогда в неравенстве треугольника для точек
. Тогда в неравенстве треугольника для точек  и
и  где
где  ,
, 
 называется равномерной сходимостью.Сходимость по (метрике) норме пространства
называется равномерной сходимостью.Сходимость по (метрике) норме пространства  называется сходимостью в среднем.
называется сходимостью в среднем. , полны, а так как они ещё и нормированы, то все стандартные метрические пространства, кроме
, полны, а так как они ещё и нормированы, то все стандартные метрические пространства, кроме  .
.  То, что это метрическое пространство, следует из того, что
То, что это метрическое пространство, следует из того, что  . Пусть по метрике пространства
. Пусть по метрике пространства  последовательность
последовательность  , то есть
, то есть  . Но тогда это выполняется и для всех других
. Но тогда это выполняется и для всех других  , то есть
, то есть  равномерно (номер
равномерно (номер  обеспечивает сходимость
обеспечивает сходимость  для всех
для всех  сразу. Но тогда по теореме Вейерштрасса предел равномерно сходящейся последовательности непрерывных функций есть функция непрерывная, то есть функция
сразу. Но тогда по теореме Вейерштрасса предел равномерно сходящейся последовательности непрерывных функций есть функция непрерывная, то есть функция  и пространство
и пространство  полно.
полно. 
 полного метрического пространства
полного метрического пространства  является полным пространством.
является полным пространством. фундаментальна в пространстве
фундаментальна в пространстве  . Тогда она будет фундаментальной и в пространстве
. Тогда она будет фундаментальной и в пространстве  . Поскольку множество
. Поскольку множество 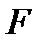 замкнуто, то точка
замкнуто, то точка  предельная для множества
предельная для множества  , что и доказывает полноту пространства
, что и доказывает полноту пространства  .
.  . Оно, очевидно, не замкнуто и не полно. Пусть
. Оно, очевидно, не замкнуто и не полно. Пусть  . Это множество не замкнуто, хотя состоит из бесконечного числа замкнутых множеств, так как не любая последовательность из этого множества сходится к пределу, ему принадлежащему. Но оно не полно, так как предел этой последовательности равен нулю, которого нет в множестве
. Это множество не замкнуто, хотя состоит из бесконечного числа замкнутых множеств, так как не любая последовательность из этого множества сходится к пределу, ему принадлежащему. Но оно не полно, так как предел этой последовательности равен нулю, которого нет в множестве  .
. при
при  .
.  , покажем, что
, покажем, что  .
.  Пусть при каком-то
Пусть при каком-то 
 . Тогда в силу непрерывности эта ситуация должна сохраниться и в
. Тогда в силу непрерывности эта ситуация должна сохраниться и в  окрестности точки
окрестности точки  .
. 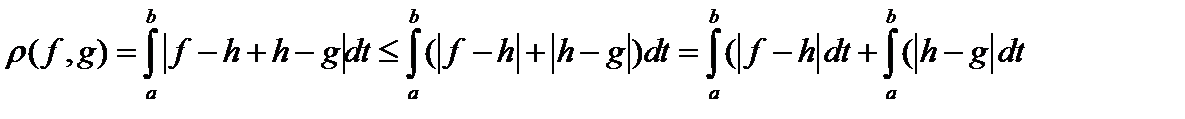 .
. , то есть
, то есть  , где
, где  . Выберем
. Выберем  тогда
тогда  . На участке вне
. На участке вне  функции совпадают и равны единице, то есть
функции совпадают и равны единице, то есть  и, таким образом, последовательность
и, таким образом, последовательность  фундаментальна. Ясно, что её пределом будет функция
фундаментальна. Ясно, что её пределом будет функция  В самом деле,
В самом деле,  , то есть последовательность
, то есть последовательность  разрывна,
разрывна,  . Это и означает неполноту пространства
. Это и означает неполноту пространства  .
. 
 да. Но для этого иногда нужно идти на коренной пересмотр ситуации. В частности, пространство функций, интегрируемых по Риману, пополнить невозможно, поэтому для того, чтобы сделать пространство
да. Но для этого иногда нужно идти на коренной пересмотр ситуации. В частности, пространство функций, интегрируемых по Риману, пополнить невозможно, поэтому для того, чтобы сделать пространство  , если
, если  в
в 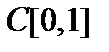 и
и  ?
?  . В пространстве
. В пространстве  . Тогда
. Тогда  .
.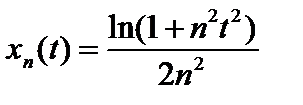 в пространстве
в пространстве  ?
?
 .
.  В дискретном метрическом пространстве все точки изолированные, поэтому фундаментальной последовательностью может быть только стационарная, которая всегда сходится.
В дискретном метрическом пространстве все точки изолированные, поэтому фундаментальной последовательностью может быть только стационарная, которая всегда сходится. 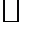
 в пространстве C [0,2], если он существует.
в пространстве C [0,2], если он существует.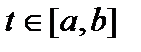 . Заданная последовательность при заданном t сходится к функции a(t)=t. Данная функция непрерывна.
. Заданная последовательность при заданном t сходится к функции a(t)=t. Данная функция непрерывна. . По определению нормы:
. По определению нормы: 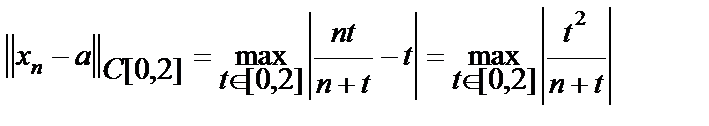 . Вычислим максимум функции
. Вычислим максимум функции  на отрезке [0,2]. Для этого вычислим критические точки.
на отрезке [0,2]. Для этого вычислим критические точки.  Таким образом, точками, подозрительными на экстремум, являются точки
Таким образом, точками, подозрительными на экстремум, являются точки  . Поскольку
. Поскольку 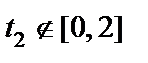 , поэтому остается лишь точка
, поэтому остается лишь точка  . Вычислим также значение функции на концах отрезка:
. Вычислим также значение функции на концах отрезка: . То есть
. То есть  . Это означает, что последовательность
. Это означает, что последовательность  в пространстве C [0,2] сходится к функции a(t)=t.
в пространстве C [0,2] сходится к функции a(t)=t.  в пространстве C [0,1], если он существует.
в пространстве C [0,1], если он существует. . Вычислим
. Вычислим  . Так как
. Так как  , то
, то  , если
, если  . Точкой, подозрительной на экстремум, является и точка
. Точкой, подозрительной на экстремум, является и точка  . Непосредственной проверкой убеждаемся, что максимум достигается в точке
. Непосредственной проверкой убеждаемся, что максимум достигается в точке  . Поэтому
. Поэтому  . Значит, последовательность
. Значит, последовательность  в пространстве C [0,1] не сходится.
в пространстве C [0,1] не сходится.  в пространстве
в пространстве  ?
? является наличие покоординатного предела. Выпишем несколько членов последовательности:
является наличие покоординатного предела. Выпишем несколько членов последовательности:  . Ясно, что последовательность
. Ясно, что последовательность  покоординатно сходится к точке
покоординатно сходится к точке  . Заметим, что
. Заметим, что  , т.к.
, т.к.  . Покажем, что последовательность
. Покажем, что последовательность  :
: при
при  .
. .
.  в пространстве
в пространстве  .
. является покоординатным пределом последовательности, но
является покоординатным пределом последовательности, но  , т.к. ряд, составленный из единиц, не является сходящимся. Следовательно, последовательность
, т.к. ряд, составленный из единиц, не является сходящимся. Следовательно, последовательность  не имеет предела.
не имеет предела.  сходится поточечно к функции
сходится поточечно к функции  для всех
для всех  , но не сходится в пространстве
, но не сходится в пространстве  .
. при каждом фиксированном
при каждом фиксированном  стремится к нулю, так как
стремится к нулю, так как  . Вычислим
. Вычислим . Значит, последовательность
. Значит, последовательность  не сходится в пространстве
не сходится в пространстве  .
. 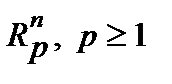 , полное.
, полное.  фундаментальная последовательность в
фундаментальная последовательность в  . Тогда
. Тогда  . Отсюда следует покоординатная сходимость
. Отсюда следует покоординатная сходимость  и, следовательно, фундаментальность числовых последовательностей
и, следовательно, фундаментальность числовых последовательностей  . Но пространство действительных чисел полное и последовательности
. Но пространство действительных чисел полное и последовательности  .
. .
. ?
?  сходится к нулю.
сходится к нулю.


 . Ясно, что покоординатно последовательность
. Ясно, что покоординатно последовательность 
 не является замкнутым, так как, например, функцию
не является замкнутым, так как, например, функцию  можно приблизить частичными суммами ряда Тейлора, которые являются алгебраическими многочленами. Следовательно, множество всех многочленов в пространстве не содержит всех предельных точек, и, значит, оно не является замкнутым.
можно приблизить частичными суммами ряда Тейлора, которые являются алгебраическими многочленами. Следовательно, множество всех многочленов в пространстве не содержит всех предельных точек, и, значит, оно не является замкнутым. хоть одна последовательность, которая сходится по норме ρ2, но не сходится по норме ρ1.
хоть одна последовательность, которая сходится по норме ρ2, но не сходится по норме ρ1. или
или  .
. Рассмотрим нормированное пространство
Рассмотрим нормированное пространство  ,
,  , система векторов
, система векторов  образует базис в нём, то есть
образует базис в нём, то есть . Эвклидова норма
. Эвклидова норма  , а
, а 
 ещё одна норма в этом пространстве. Оценим её.
ещё одна норма в этом пространстве. Оценим её.  . Обозначив
. Обозначив  , получим
, получим  . Покажем, что
. Покажем, что  в свою очередь подчинена
в свою очередь подчинена 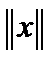 . Рассмотрим функцию
. Рассмотрим функцию  переменных
переменных  на сфере
на сфере 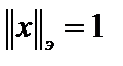 . Она непрерывна, так как
. Она непрерывна, так как  и стремится к нулю при
и стремится к нулю при  . Единичная сфера
. Единичная сфера 
 замкнутое ограниченное множество, поэтому на ней, в соответствии с теоремой Вейерштрасса, функция достигает своих точных верхней и нижней граней. То есть на сфере
замкнутое ограниченное множество, поэтому на ней, в соответствии с теоремой Вейерштрасса, функция достигает своих точных верхней и нижней граней. То есть на сфере  имеем
имеем  .
.  пространства
пространства  сильнее метрики
сильнее метрики  пространства
пространства 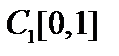 .
. , то есть
, то есть  стандартный пробник функционального анализа,
стандартный пробник функционального анализа,  .
. 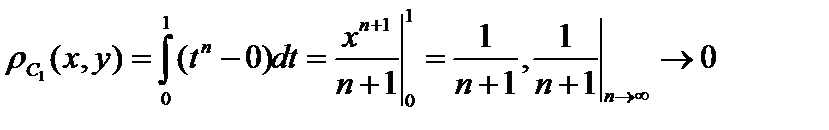 , а
, а  , то есть эта последовательность сходится по
, то есть эта последовательность сходится по  отображение между метрическими пространствами не только взаимно однозначно, но и взаимно непрерывно, то есть гомеоморфно. В конечномерных пространствах все метрики (нормы)топологически эквивалентныв следующем смысле: для шара
отображение между метрическими пространствами не только взаимно однозначно, но и взаимно непрерывно, то есть гомеоморфно. В конечномерных пространствах все метрики (нормы)топологически эквивалентныв следующем смысле: для шара  радиуса R с центром в точке
радиуса R с центром в точке  , построенного на основе одной из норм, можно построить вписанный в него и описанный вокруг него шары, построенные на основе другой нормы (разумеется, другого радиуса). В бесконечномерных пространствах это не так.
, построенного на основе одной из норм, можно построить вписанный в него и описанный вокруг него шары, построенные на основе другой нормы (разумеется, другого радиуса). В бесконечномерных пространствах это не так.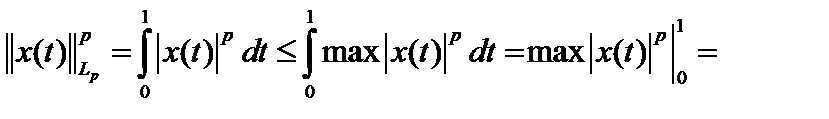
 , но
, но 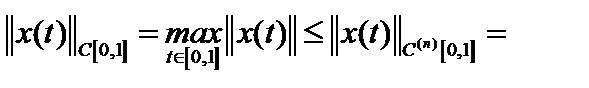

 .
. 
 , если
, если  , то есть любой элемент из множества
, то есть любой элемент из множества  , то есть совпадает со всем носителем метрического пространства
, то есть совпадает со всем носителем метрического пространства  , то множество M называется всюду плотным (абсолютно плотным) в множестве
, то множество M называется всюду плотным (абсолютно плотным) в множестве  в любой, сколь угодно малой окрестности точки
в любой, сколь угодно малой окрестности точки  найдутся точки из множества M, то есть все точки
найдутся точки из множества M, то есть все точки  есть точки прикосновения множества M, то есть замыкание множества M совпадает со всем пространством.
есть точки прикосновения множества M, то есть замыкание множества M совпадает со всем пространством.
 шар, не содержащий точек из множества M.
шар, не содержащий точек из множества M. Множество рациональных чисел всюду плотно на действительной оси.
Множество рациональных чисел всюду плотно на действительной оси. Множество целых чисел нигде не плотно на действительной оси.
Множество целых чисел нигде не плотно на действительной оси. Любое дискретное множество нигде не плотно в пространстве.
Любое дискретное множество нигде не плотно в пространстве.  Любая изолированная точка есть нигде не плотное множество.
Любая изолированная точка есть нигде не плотное множество. Любое подмножество нигде не плотного множества нигде не плотно.
Любое подмножество нигде не плотного множества нигде не плотно. Объединение конечного числа нигде не плотных множеств нигде не плотно.
Объединение конечного числа нигде не плотных множеств нигде не плотно. Объединение счётного числа нигде не плотных множеств уже не нигде не плотно. Оно может быть даже всюду плотно. Множество рациональных чисел
Объединение счётного числа нигде не плотных множеств уже не нигде не плотно. Оно может быть даже всюду плотно. Множество рациональных чисел  счётное всюду плотное множество на действительной оси, но оно есть объединение счётного числа изолированных точек.
счётное всюду плотное множество на действительной оси, но оно есть объединение счётного числа изолированных точек. сепарабельно, если в нём существует счётное всюду плотное множество
сепарабельно, если в нём существует счётное всюду плотное множество 
 из неё можно выделить (separate (лат)
из неё можно выделить (separate (лат)  выделять) подпоследовательность
выделять) подпоследовательность  , сходящуюся к
, сходящуюся к  .
. Эвклидово пространство
Эвклидово пространство  сепарабельно. Счётный скелет в нём
сепарабельно. Счётный скелет в нём  множество точек с рациональными координатами.
множество точек с рациональными координатами. Дискретное метрическое пространство, состоящее из счётного числа точек, сепарабельно.
Дискретное метрическое пространство, состоящее из счётного числа точек, сепарабельно.  Пространство
Пространство  сепарабельно.
сепарабельно.  Пространство
Пространство  сепарабельно.
сепарабельно.  всех последовательностей с рациональными членами, у которых только конечное, для каждого своё, число членов не равно нулю, а остальные члены нулевые. Это счётное множество, как объединение счётного числа счётных множеств. Покажем, что множество
всех последовательностей с рациональными членами, у которых только конечное, для каждого своё, число членов не равно нулю, а остальные члены нулевые. Это счётное множество, как объединение счётного числа счётных множеств. Покажем, что множество  . Так как
. Так как  , то есть ряд сходится, то
, то есть ряд сходится, то 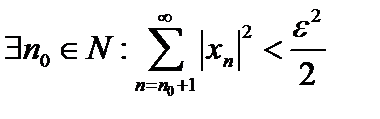 . Так как множество рациональных чисел
. Так как множество рациональных чисел  всюду плотно на числовой оси, то. Нормировочный множитель выбран для удобства и в си
всюду плотно на числовой оси, то. Нормировочный множитель выбран для удобства и в си  лу произвольности
лу произвольности  . Рассмотрим последовательность
. Рассмотрим последовательность  , члены которой при
, члены которой при  равны нулю. Тогда расстояние между
равны нулю. Тогда расстояние между  и
и 
 , то есть
, то есть  , то есть замыкание
, то есть замыкание  Пространство
Пространство  (
(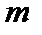 ) не сепарабельно.
) не сепарабельно.  . Тогда
. Тогда  двоичное представление числа, а множество всех таких чисел имеет мощность континуума. В метрике
двоичное представление числа, а множество всех таких чисел имеет мощность континуума. В метрике  . Пусть пространство
. Пусть пространство  . Всего элементов
. Всего элементов  .
.  счётный скелет пространства
счётный скелет пространства 


