Полнота системы векторов в смысле Стеклова
Теорема 1. (О линейной независимости ортогональных векторов). Пусть  Тогда система векторов Тогда система векторов  линейно независима. линейно независима.
 . Составим линейную комбинацию . Составим линейную комбинацию  и умножим её скалярно на и умножим её скалярно на  : :  , но , но  . . 
Определение 1. Система векторов  или или   символ Кронекера, называется ортонормированной (ОНС). символ Кронекера, называется ортонормированной (ОНС).
Определение 2. Для произвольного элемента  произвольного бесконечномерного евклидова пространства и произвольной ортонормированной системы элементов произвольного бесконечномерного евклидова пространства и произвольной ортонормированной системы элементов  рядом Фурье элемента рядом Фурье элемента  по системе по системе 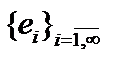 называется формально составленная бесконечная сумма (ряд) вида называется формально составленная бесконечная сумма (ряд) вида 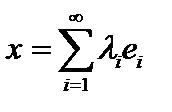 в которой действительные числа в которой действительные числа 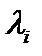 называемые коэффициентами Фурье элемента называемые коэффициентами Фурье элемента  по системе по системе 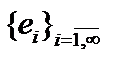 , где , где 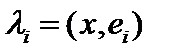 . .
Комментарий. Умножив элемент  скалярно на скалярно на  и сразу получим, что и сразу получим, что 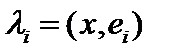 . Естественно, возникает вопрос о сходимости этого ряда. Для исследования этого вопроса зафиксируем произвольный номер . Естественно, возникает вопрос о сходимости этого ряда. Для исследования этого вопроса зафиксируем произвольный номер  и выясним, что отличает и выясним, что отличает  -ю частичную сумму ряда Фурье от любой другой линейной комбинации -ю частичную сумму ряда Фурье от любой другой линейной комбинации  первых первых  элементов ортонормированной системы элементов ортонормированной системы 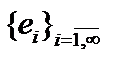 . .
Теорема 2. Для любого фиксированного номера  среди всех сумм вида среди всех сумм вида  наименьшее отклонение от элемента наименьшее отклонение от элемента  по норме данного евклидова пространства имеет n-я частичная сумма ряда Фурье элемента по норме данного евклидова пространства имеет n-я частичная сумма ряда Фурье элемента 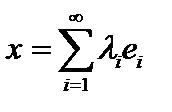 при при  . .
 Учитывая ортонормированность системы Учитывая ортонормированность системы 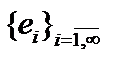 иопределение коэффициента Фурье, можно записать иопределение коэффициента Фурье, можно записать 
Минимум этого выражения при  так как при этом всегда неотрицательная первая сумма в правой части обращается в нуль, а остальные слагаемые от так как при этом всегда неотрицательная первая сумма в правой части обращается в нуль, а остальные слагаемые от  не зависят. не зависят. 
Пример. Рассмотрим тригонометрическую систему: 
в пространстве всех интегрируемых по Риману функций  на сегменте на сегменте  . Легко проверить, что это ОНС, и тогда Ряд Фурье функции . Легко проверить, что это ОНС, и тогда Ряд Фурье функции  имеет вид: имеет вид:  где где
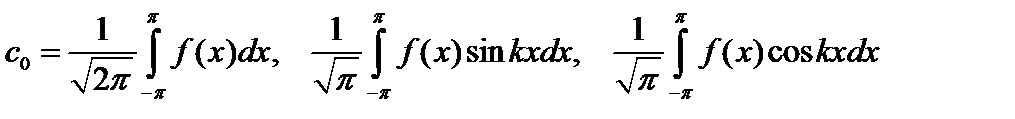 . .
Комментарий. Тригонометрический ряд Фурье обычно записывают в виде:  . Тогда . Тогда  . .
Произвольная ОНС в бесконечномерном эвклидовом пространстве без дополнительных предположений, вообще говоря, не является базисом этого пространства. Рассмотрим ОНС 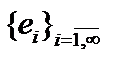 где где   символ Кронекера. в произвольном бесконечномерном эвклидовом пространстве символ Кронекера. в произвольном бесконечномерном эвклидовом пространстве  . Пусть . Пусть  – подпространство эвклидова пространства, а – подпространство эвклидова пространства, а   подпространство, ортогональное к подпространство, ортогональное к  . Тогда эвклидово пространство . Тогда эвклидово пространство  . Проекция вектора . Проекция вектора  на на   вектор вектор  , где , где  . .

Мы будем искать те значения коэффициентов разложения 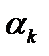 , при которых невязка (квадрат невязки) , при которых невязка (квадрат невязки)  будет минимальна: будет минимальна:

 . .
Ясно, что это выражение будет принимать минимальное значение при  , что тривиально, и при , что тривиально, и при  . .  Тогда Тогда  . Отсюда получаем неравенство Бесселя . Отсюда получаем неравенство Бесселя 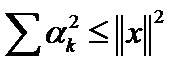 . При . При 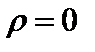 ортонормированная система векторов (ОНС) называется полной ортонормированной системой в смысле Стеклова (ПОНС). Отсюда можно получить равенство Стеклова – Парсеваля ортонормированная система векторов (ОНС) называется полной ортонормированной системой в смысле Стеклова (ПОНС). Отсюда можно получить равенство Стеклова – Парсеваля 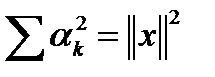  теорему Пифагора для полныхв смысле Стеклова бесконечномерных эвклидовых пространств. теорему Пифагора для полныхв смысле Стеклова бесконечномерных эвклидовых пространств.
Определение 3. ОНС, для которой выполняется равенство Стеклова–Парсеваля  называется полной ортонормированной системой в смысле Стеклова (ПОНС). называется полной ортонормированной системой в смысле Стеклова (ПОНС).
Определение 4. ПОНС называется ортонормированным базисом пространства (ОНБ). Определение 5. Полная ортонормированная система называется ортонормированным базисом пространства.
Пример. В эвклидовом пространстве последовательностей комплексных чисел  ОНБ образует система векторов ОНБ образует система векторов 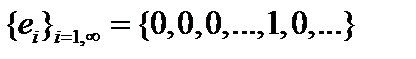 . Рассмотрим для . Рассмотрим для  частичную сумму ряда частичную сумму ряда  . Тогда . Тогда  как хвост сходящегося ряда. Таким образом, система векторов как хвост сходящегося ряда. Таким образом, система векторов  является ПОНС и образуетОНБ. является ПОНС и образуетОНБ.
Пример. Тригонометрическая система 
в пространстве всех интегрируемых по Риману функций  на сегменте на сегменте  является ПОНС и образуетОНБ. является ПОНС и образуетОНБ.
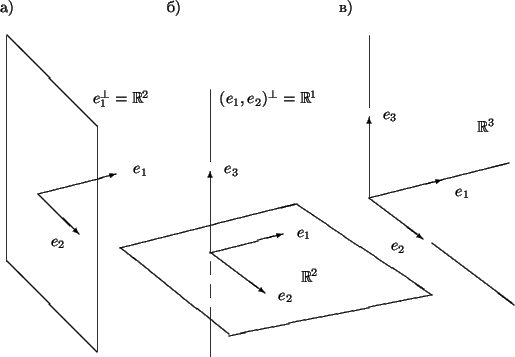
Комментарий. Если  – полная система векторов, то не существует отличных от нуля векторов из – полная система векторов, то не существует отличных от нуля векторов из  , ей ортогональных, так как из , ей ортогональных, так как из  для всех для всех  следует следует  . Пусть . Пусть  . Выберем некоторый вектор . Выберем некоторый вектор  . Он, очевидно, не образует полной системы векторов. Подпространство, им порождаемое, есть . Он, очевидно, не образует полной системы векторов. Подпространство, им порождаемое, есть  , а ортогональное дополнение отлично от нуля и представляет собой плоскость, проходящую через нуль перпендикулярно , а ортогональное дополнение отлично от нуля и представляет собой плоскость, проходящую через нуль перпендикулярно  (см. рис.а). Выберем в этой плоскости, то есть в ортогональном дополнении, элемент (см. рис.а). Выберем в этой плоскости, то есть в ортогональном дополнении, элемент 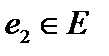 и образуем последовательность и образуем последовательность  . Она также не полна и порождает пространство . Она также не полна и порождает пространство  , то есть плоскость, а ортогональное дополнение к ней вновь не нуль, а представляет собой прямую, перпендикулярную этой плоскости (см. рис.б). И наконец, когда мы выберем на этой прямой третий вектор , то есть плоскость, а ортогональное дополнение к ней вновь не нуль, а представляет собой прямую, перпендикулярную этой плоскости (см. рис.б). И наконец, когда мы выберем на этой прямой третий вектор  , то последовательность , то последовательность  станет полной, будет порождать пространство станет полной, будет порождать пространство  , а ортогональное дополнение к ней станет нулевым (рис. в). , а ортогональное дополнение к ней станет нулевым (рис. в).
Теорема 3 (Грамм  Шмидт об ортогонализации). Пусть Шмидт об ортогонализации). Пусть   линейно независимая система векторов эвклидова пространства линейно независимая система векторов эвклидова пространства  . Тогда в пространстве . Тогда в пространстве  существует ОНБ существует ОНБ  . .
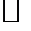 Построим этот базис. Обозначим Построим этот базис. Обозначим  . Построим . Построим  и выберем и выберем  так, чтобы так, чтобы 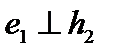 , то есть , то есть 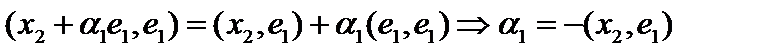 . Тогда . Тогда  . Построим вектор . Построим вектор  таким образом, чтобы таким образом, чтобы  Тогда Тогда  , а , а  Продолжая процедуру, получим Продолжая процедуру, получим  .Эту формулу следует доказать методом матиндукции. .Эту формулу следует доказать методом матиндукции. 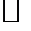
Пример. 1. Любую ортогональную систему векторов можно дополнить до ОНБ. Дополнить совокупность векторов 1)  2) 2)  до ОНБ. до ОНБ.
2. Найти ОНБ линейной оболочки:  . .
3. Ортогонализировать векторы  в пространстве в пространстве  , показав их линейную независимость. (Совокупность функций , показав их линейную независимость. (Совокупность функций  линейно независима линейно независима  , если и только если её вронскиан , если и только если её вронскиан  не равен нулю.) не равен нулю.)
Комментарий. Ортогонализированная система векторов  в в  называется полиномами Лежандра: называется полиномами Лежандра:  , которые появляются при решении многих задач математической физики. , которые появляются при решении многих задач математической физики.
4. Ортогонализировать в  систему векторов систему векторов 
Полнота в смысле Фреше
Определение 1. Последовательность точек  эвклидова пространства сходится по норме к точке эвклидова пространства сходится по норме к точке  , если числовая последовательность , если числовая последовательность  , то есть , то есть 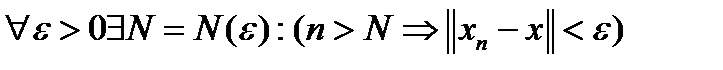 . Обозначение используется обычное: . Обозначение используется обычное:  . .
Определение 2. Пусть множество M есть подмножество множества Е. Точка  называется предельной точкой множества M, если существует последовательность точек множества M, с попарно различными элементами, сходящаяся к x. называется предельной точкой множества M, если существует последовательность точек множества M, с попарно различными элементами, сходящаяся к x.
Комментарий. Чтобы точка  была предельнойточкой множества M, надо каким была предельнойточкой множества M, надо каким  либо образом исключить стационарные последовательности либо образом исключить стационарные последовательности  , чтобы изолированные точки множества , чтобы изолированные точки множества  , то есть точки, у которых существует окрестность, не содержащая точек из множества , то есть точки, у которых существует окрестность, не содержащая точек из множества  , не могли оказаться предельными. В этом определении представлен один из таких вариантов. , не могли оказаться предельными. В этом определении представлен один из таких вариантов.
Определение 3. Пусть множество  . Множество . Множество  называется замыканием множества называется замыканием множества  , если для любой точки , если для любой точки 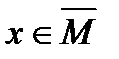 существует последовательность не обязательно различных точек из множества существует последовательность не обязательно различных точек из множества  , сходящихся к точке х. , сходящихся к точке х.
Определение 4. Множество называется замкнутым, если оно совпадает со своим замыканием то есть  . .
Комментарий. В определении допускаются стационарные, начиная с некоторого номера, последовательности. Поэтому любая изолированная точка множества  замкнута. Позже мы рассмотрим этот вопрос подробнее. замкнута. Позже мы рассмотрим этот вопрос подробнее.
Определение 5. Последовательность точек xn эвклидова пространства  называется фундаментальной, если называется фундаментальной, если  . .
Определение 5*. Последовательность точек xn эвклидова пространства  называется фундаментальной, если называется фундаментальной, если 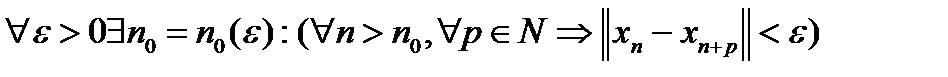 . .
Теорема 1. Последовательность точек  эвклидова пространства фундаментальна, если она сходится по норме к точке эвклидова пространства фундаментальна, если она сходится по норме к точке  . .
 Пусть Пусть  . Тогда . Тогда  . Выберем произвольные . Выберем произвольные  . Тогда из неравенства треугольника . Тогда из неравенства треугольника  . . 
Комментарий. Обратное, вообще говоря, неверно. Рассмотрим примеры.
Примеры. 1. Рассмотрим в пространстве всех интегрируемых по Риману функций  на сегменте на сегменте  подпространство, состоящее из всех многочленов. Пусть подпространство, состоящее из всех многочленов. Пусть 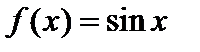 . Согласно формуле Тейлора с остаточным членом в форме Лагранжа можем записать . Согласно формуле Тейлора с остаточным членом в форме Лагранжа можем записать  , где , где  .Обозначим через Pn (x) сумму первых n +1 членов в правой части этой формулы. Тогда Pn (x) есть многочлен степени n, причем .Обозначим через Pn (x) сумму первых n +1 членов в правой части этой формулы. Тогда Pn (x) есть многочлен степени n, причем  при при  .То есть последовательность Pn лежит в подпространстве многочленов, сходится к функции .То есть последовательность Pn лежит в подпространстве многочленов, сходится к функции 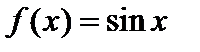 , но предельная функция не лежит в пространстве многочленов , но предельная функция не лежит в пространстве многочленов  синуса среди многочленов нет… Следовательно, рассматриваемое подпространство незамкнуто, хотя последовательность Pn (x) фундаментальна (хотя бы потому, что сходится). Причина в том, что мы из пространства выбросили часть функций, так что в оставшейся части образовались ”дырки”, одной из которых и является синус. синуса среди многочленов нет… Следовательно, рассматриваемое подпространство незамкнуто, хотя последовательность Pn (x) фундаментальна (хотя бы потому, что сходится). Причина в том, что мы из пространства выбросили часть функций, так что в оставшейся части образовались ”дырки”, одной из которых и является синус.
2. Такой же пример даёт множество рациональных чисел, рассматриваемое как подмножество числовой оси 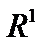 . Последовательность Бернулли . Последовательность Бернулли  , но числа , но числа  среди рациональных чисел нет. среди рациональных чисел нет.
Определение 6. Эвклидово пространство  называется полным (в смысле Фреше), если всякая его фундаментальная последовательность сходится. называется полным (в смысле Фреше), если всякая его фундаментальная последовательность сходится.
Определение 9. Полное бесконечномерное эвклидово пространство называется гильбертовым.
Комментарий. Понятие полноты и в том и в другом случае, по сути, означает, что элементов, будь то пространства, или последовательности векторов, или еще чего-нибудь, должно быть достаточным для того, чтобы некоторое свойство выполнялось.
Нормированные пространства
Заметим, что эвклидова норма  обладает очевидными свойствами: обладает очевидными свойствами:
-
 ; ; -
 для любого для любого  и любого числа и любого числа  ; ; -
 для любых для любых  (неравенство треугольника). (неравенство треугольника). Неотрицательность и положительная однородность функционала  очевидны. Покажем неравенство треугольника: очевидны. Покажем неравенство треугольника:

Приняв эти свойства за аксиомы, получим следующее
Определение 1. Говорят, что на линейной структуре  задана норма задана норма 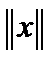 его элементов, если указан функционал, ставящий в соответствие этим элементам действительное число, удовлетворяющее аксиомам 1-3. Пара его элементов, если указан функционал, ставящий в соответствие этим элементам действительное число, удовлетворяющее аксиомам 1-3. Пара  называется нормированным пространством. называется нормированным пространством.
Определение 2. Полное бесконечномерное нормированное пространство называется банаховым.
Пример. Доказать, что  , где , где  нормированное пространство, нормированное пространство,
выполняется неравенство  . . 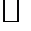
 . . 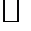
Комментарий. 1. Ясно, что любое эвклидово пространство нормировано. Обратное, вообще говоря, неверно  эвклидова норма просто одна из многих. 2. Обратим внимание, что и гильбертовы пространства какполные бесконечномерные эвклидовы пространства и банаховы пространствакак полные бесконечномерные нормированные пространства построены на линейных структурах. Сейчас мы начнём строить пространства на произвольных носителях. эвклидова норма просто одна из многих. 2. Обратим внимание, что и гильбертовы пространства какполные бесконечномерные эвклидовы пространства и банаховы пространствакак полные бесконечномерные нормированные пространства построены на линейных структурах. Сейчас мы начнём строить пространства на произвольных носителях.
Метрические пространства
Комментарий. Теорию метрических пространств построил ученик Ж. Адамара, автора как термина функционал, так и термина функциональный анализ, М. Фреше. Он обобщил понятие расстояния, используемого в аналитической геометрии при изучении свойств геометрических объектов и в математическом анализе при определении предела числовой последовательности или функции.
Определение 1. Пусть  – произвольное непустое множество. Говорят, что на – произвольное непустое множество. Говорят, что на  задана метрика (расстояние) задана метрика (расстояние)  , если каждой паре элементов , если каждой паре элементов  поставлено в соответствие единственное неотрицательное число(неотрицательный функционал) поставлено в соответствие единственное неотрицательное число(неотрицательный функционал)  , удовлетворяющее следующим аксиомам: , удовлетворяющее следующим аксиомам:
1)  (аксиома тождества); (аксиома тождества);
2)  (аксиома треугольника). (аксиома треугольника).
Пара 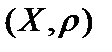 , то есть множество , то есть множество  с заданной на нем метрикой с заданной на нем метрикой  , называется метрическим пространством. , называется метрическим пространством.
Комментарий. 1.Из неравенства треугольника при  сразу получаем сразу получаем  , а при , а при 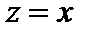 сразу получаем сразу получаем 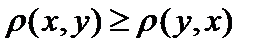 Но с другой стороны, неравенство треугольника можно записать так: Но с другой стороны, неравенство треугольника можно записать так: 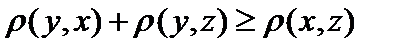 . Тогда при . Тогда при  сразу получаем сразу получаем  , то есть , то есть  . Тогда исходная система аксиом заменяется на часто более удобную систему из трёх аксиом: . Тогда исходная система аксиом заменяется на часто более удобную систему из трёх аксиом: 
Определение 2. Если 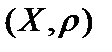 – метрическое пространство и – метрическое пространство и  , то пара , то пара  также будет являться метрическим пространством и называется подпространством пространства также будет являться метрическим пространством и называется подпространством пространства 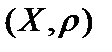 , если , если  , то есть расстояние между точками , то есть расстояние между точками  – равно расстоянию между этими точками в пространстве – равно расстоянию между этими точками в пространстве 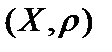 . .
Комментарий. Стандартные метрические пространства – это метрические пространства со стандартными носителями и со стандартными метриками. В этих случаях пространства носят стандартные названия.
Стандартные носители
1.Кортежи  ; ;
2. Ограниченные последовательности 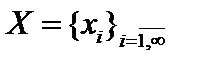 , то есть , то есть  . .
3. Множество непрерывных или непрерывно дифференцируемых функций  на сегменте на сегменте  . .
Стандартные метрики
1. Гёльдеровские (радикальные) метрики:  или или  или или 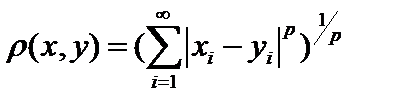 , ,  .При .При  эти метрики иногда называют энергетическими, так как в прикладных задачах они связана с энергией. Ряд, задающий эти метрики иногда называют энергетическими, так как в прикладных задачах они связана с энергией. Ряд, задающий  , в этом случае сходится, так как , в этом случае сходится, так как  , то есть , то есть  . .
2. Чебышевские (супремальные), или равномерные метрики. 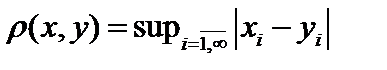 или или 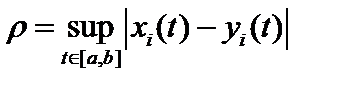 . .
|



 Тогда система векторов
Тогда система векторов  линейно независима.
линейно независима.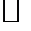 . Составим линейную комбинацию
. Составим линейную комбинацию  и умножим её скалярно на
и умножим её скалярно на  :
:  , но
, но  .
.  или
или 
 символ Кронекера, называется ортонормированной (ОНС).
символ Кронекера, называется ортонормированной (ОНС). произвольного бесконечномерного евклидова пространства и произвольной ортонормированной системы элементов
произвольного бесконечномерного евклидова пространства и произвольной ортонормированной системы элементов  рядом Фурье элемента
рядом Фурье элемента 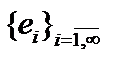 называется формально составленная бесконечная сумма (ряд) вида
называется формально составленная бесконечная сумма (ряд) вида 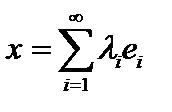 в которой действительные числа
в которой действительные числа 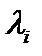 называемые коэффициентами Фурье элемента
называемые коэффициентами Фурье элемента 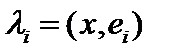 .
. и сразу получим, что
и сразу получим, что  и выясним, что отличает
и выясним, что отличает  первых
первых  .
.
 так как при этом всегда неотрицательная первая сумма в правой части обращается в нуль, а остальные слагаемые от
так как при этом всегда неотрицательная первая сумма в правой части обращается в нуль, а остальные слагаемые от  не зависят.
не зависят. 
 на сегменте
на сегменте  . Легко проверить, что это ОНС, и тогда Ряд Фурье функции
. Легко проверить, что это ОНС, и тогда Ряд Фурье функции  где
где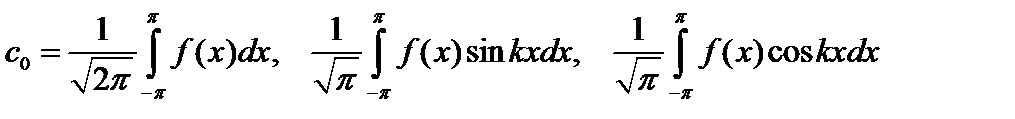 .
. . Тогда
. Тогда  .
. . Пусть
. Пусть  – подпространство эвклидова пространства, а
– подпространство эвклидова пространства, а 
 подпространство, ортогональное к
подпространство, ортогональное к  . Тогда эвклидово пространство
. Тогда эвклидово пространство  . Проекция вектора
. Проекция вектора  на
на 
 вектор
вектор  , где
, где  .
.
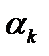 , при которых невязка (квадрат невязки)
, при которых невязка (квадрат невязки)  будет минимальна:
будет минимальна:
 .
. , что тривиально, и при
, что тривиально, и при  .
.  Тогда
Тогда  . Отсюда получаем неравенство Бесселя
. Отсюда получаем неравенство Бесселя 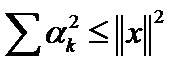 . При
. При 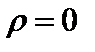 ортонормированная система векторов (ОНС) называется полной ортонормированной системой в смысле Стеклова (ПОНС). Отсюда можно получить равенство Стеклова – Парсеваля
ортонормированная система векторов (ОНС) называется полной ортонормированной системой в смысле Стеклова (ПОНС). Отсюда можно получить равенство Стеклова – Парсеваля 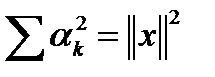
 теорему Пифагора для полныхв смысле Стеклова бесконечномерных эвклидовых пространств.
теорему Пифагора для полныхв смысле Стеклова бесконечномерных эвклидовых пространств. называется полной ортонормированной системой в смысле Стеклова (ПОНС).
называется полной ортонормированной системой в смысле Стеклова (ПОНС). ОНБ образует система векторов
ОНБ образует система векторов 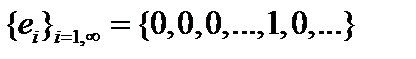 . Рассмотрим для
. Рассмотрим для  частичную сумму ряда
частичную сумму ряда  . Тогда
. Тогда  как хвост сходящегося ряда. Таким образом, система векторов
как хвост сходящегося ряда. Таким образом, система векторов  является ПОНС и образуетОНБ.
является ПОНС и образуетОНБ. – полная система векторов, то не существует отличных от нуля векторов из
– полная система векторов, то не существует отличных от нуля векторов из  , ей ортогональных, так как из
, ей ортогональных, так как из  для всех
для всех  следует
следует  . Пусть
. Пусть  . Выберем некоторый вектор
. Выберем некоторый вектор  . Он, очевидно, не образует полной системы векторов. Подпространство, им порождаемое, есть
. Он, очевидно, не образует полной системы векторов. Подпространство, им порождаемое, есть  , а ортогональное дополнение отлично от нуля и представляет собой плоскость, проходящую через нуль перпендикулярно
, а ортогональное дополнение отлично от нуля и представляет собой плоскость, проходящую через нуль перпендикулярно  (см. рис.а). Выберем в этой плоскости, то есть в ортогональном дополнении, элемент
(см. рис.а). Выберем в этой плоскости, то есть в ортогональном дополнении, элемент 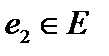 и образуем последовательность
и образуем последовательность  . Она также не полна и порождает пространство
. Она также не полна и порождает пространство  , то есть плоскость, а ортогональное дополнение к ней вновь не нуль, а представляет собой прямую, перпендикулярную этой плоскости (см. рис.б). И наконец, когда мы выберем на этой прямой третий вектор
, то есть плоскость, а ортогональное дополнение к ней вновь не нуль, а представляет собой прямую, перпендикулярную этой плоскости (см. рис.б). И наконец, когда мы выберем на этой прямой третий вектор  , то последовательность
, то последовательность  станет полной, будет порождать пространство
станет полной, будет порождать пространство 
 Шмидт об ортогонализации). Пусть
Шмидт об ортогонализации). Пусть 
 Построим этот базис. Обозначим
Построим этот базис. Обозначим  . Построим
. Построим  и выберем
и выберем  так, чтобы
так, чтобы 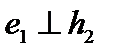 , то есть
, то есть 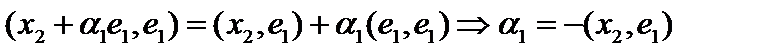 . Тогда
. Тогда  . Построим вектор
. Построим вектор  таким образом, чтобы
таким образом, чтобы  Тогда
Тогда  , а
, а  Продолжая процедуру, получим
Продолжая процедуру, получим  .Эту формулу следует доказать методом матиндукции.
.Эту формулу следует доказать методом матиндукции.  2)
2)  до ОНБ.
до ОНБ. .
. в пространстве
в пространстве  , показав их линейную независимость. (Совокупность функций
, показав их линейную независимость. (Совокупность функций  линейно независима
линейно независима  , если и только если её вронскиан
, если и только если её вронскиан  не равен нулю.)
не равен нулю.) в
в  называется полиномами Лежандра:
называется полиномами Лежандра:  , которые появляются при решении многих задач математической физики.
, которые появляются при решении многих задач математической физики.
 эвклидова пространства сходится по норме к точке
эвклидова пространства сходится по норме к точке  , если числовая последовательность
, если числовая последовательность  , то есть
, то есть 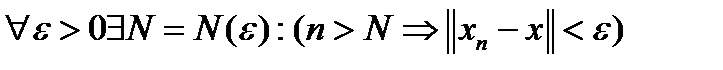 . Обозначение используется обычное:
. Обозначение используется обычное:  .
. называется предельной точкой множества M, если существует последовательность точек множества M, с попарно различными элементами, сходящаяся к x.
называется предельной точкой множества M, если существует последовательность точек множества M, с попарно различными элементами, сходящаяся к x. либо образом исключить стационарные последовательности
либо образом исключить стационарные последовательности  , чтобы изолированные точки множества
, чтобы изолированные точки множества  , то есть точки, у которых существует окрестность, не содержащая точек из множества
, то есть точки, у которых существует окрестность, не содержащая точек из множества  . Множество
. Множество  называется замыканием множества
называется замыканием множества 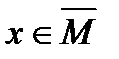 существует последовательность не обязательно различных точек из множества
существует последовательность не обязательно различных точек из множества  .
. называется фундаментальной, если
называется фундаментальной, если  .
.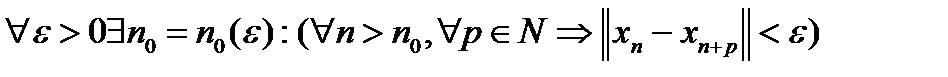 .
. Пусть
Пусть  . Тогда
. Тогда  . Выберем произвольные
. Выберем произвольные  . Тогда из неравенства треугольника
. Тогда из неравенства треугольника  .
. 
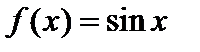 . Согласно формуле Тейлора с остаточным членом в форме Лагранжа можем записать
. Согласно формуле Тейлора с остаточным членом в форме Лагранжа можем записать  , где
, где  .Обозначим через Pn (x) сумму первых n +1 членов в правой части этой формулы. Тогда Pn (x) есть многочлен степени n, причем
.Обозначим через Pn (x) сумму первых n +1 членов в правой части этой формулы. Тогда Pn (x) есть многочлен степени n, причем  при
при  .То есть последовательность Pn лежит в подпространстве многочленов, сходится к функции
.То есть последовательность Pn лежит в подпространстве многочленов, сходится к функции  синуса среди многочленов нет… Следовательно, рассматриваемое подпространство незамкнуто, хотя последовательность Pn (x) фундаментальна (хотя бы потому, что сходится). Причина в том, что мы из пространства выбросили часть функций, так что в оставшейся части образовались ”дырки”, одной из которых и является синус.
синуса среди многочленов нет… Следовательно, рассматриваемое подпространство незамкнуто, хотя последовательность Pn (x) фундаментальна (хотя бы потому, что сходится). Причина в том, что мы из пространства выбросили часть функций, так что в оставшейся части образовались ”дырки”, одной из которых и является синус.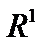 . Последовательность Бернулли
. Последовательность Бернулли  , но числа
, но числа  среди рациональных чисел нет.
среди рациональных чисел нет. обладает очевидными свойствами:
обладает очевидными свойствами: ;
; для любого
для любого  и любого числа
и любого числа  ;
; для любых
для любых  (неравенство треугольника).
(неравенство треугольника).
 задана норма
задана норма 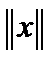 его элементов, если указан функционал, ставящий в соответствие этим элементам действительное число, удовлетворяющее аксиомам 1-3. Пара
его элементов, если указан функционал, ставящий в соответствие этим элементам действительное число, удовлетворяющее аксиомам 1-3. Пара  называется нормированным пространством.
называется нормированным пространством. , где
, где  нормированное пространство,
нормированное пространство, .
. 
 .
.  эвклидова норма просто одна из многих. 2. Обратим внимание, что и гильбертовы пространства какполные бесконечномерные эвклидовы пространства и банаховы пространствакак полные бесконечномерные нормированные пространства построены на линейных структурах. Сейчас мы начнём строить пространства на произвольных носителях.
эвклидова норма просто одна из многих. 2. Обратим внимание, что и гильбертовы пространства какполные бесконечномерные эвклидовы пространства и банаховы пространствакак полные бесконечномерные нормированные пространства построены на линейных структурах. Сейчас мы начнём строить пространства на произвольных носителях. – произвольное непустое множество. Говорят, что на
– произвольное непустое множество. Говорят, что на  , если каждой паре элементов
, если каждой паре элементов  поставлено в соответствие единственное неотрицательное число(неотрицательный функционал)
поставлено в соответствие единственное неотрицательное число(неотрицательный функционал)  , удовлетворяющее следующим аксиомам:
, удовлетворяющее следующим аксиомам: (аксиома тождества);
(аксиома тождества); (аксиома треугольника).
(аксиома треугольника).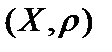 , то есть множество
, то есть множество  сразу получаем
сразу получаем  , а при
, а при 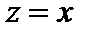 сразу получаем
сразу получаем 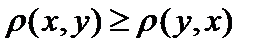 Но с другой стороны, неравенство треугольника можно записать так:
Но с другой стороны, неравенство треугольника можно записать так: 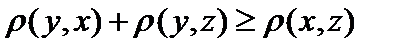 . Тогда при
. Тогда при  , то есть
, то есть  . Тогда исходная система аксиом заменяется на часто более удобную систему из трёх аксиом:
. Тогда исходная система аксиом заменяется на часто более удобную систему из трёх аксиом: 
 , то пара
, то пара  также будет являться метрическим пространством и называется подпространством пространства
также будет являться метрическим пространством и называется подпространством пространства  , то есть расстояние между точками
, то есть расстояние между точками  – равно расстоянию между этими точками в пространстве
– равно расстоянию между этими точками в пространстве  ;
;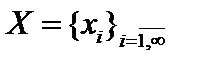 , то есть
, то есть  .
. на сегменте
на сегменте  .
. или
или  или
или 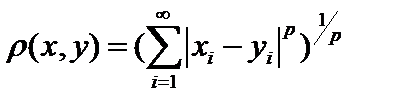 ,
,  .При
.При  эти метрики иногда называют энергетическими, так как в прикладных задачах они связана с энергией. Ряд, задающий
эти метрики иногда называют энергетическими, так как в прикладных задачах они связана с энергией. Ряд, задающий  , то есть
, то есть  .
.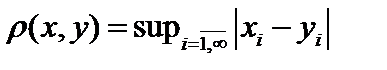 или
или 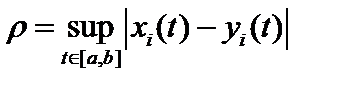 .
.


