
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сходимость в топологических пространствахСодержание книги Поиск на нашем сайте
Определение. Последовательность точек {xn} топологического пространства Х называется сходящейся к точке x0ÎX, если любая окрестность x0 содержит все точки последовательности, за исключением, быть может, их конечного числа. При этом саму точку x0 называют пределом последовательности и обозначают
Комментарий. В обычной топологии, то есть в метрических пространствах, на прямой пределом последовательности Рассмотрим прямую с топологией Зарисского. В этой топологии любая точка Обычная и дискретная топологии удовлетворяют аксиомам А1 и А2. Однако дискретная топология не очень похожа на обычную. В дискретной топологии открытым является любое множество, то есть, в частности, любая точка x является сама своей окрестностью В произвольном метрическом пространстве точка х0 тогда и только тогда принадлежит замыканию некоторого множества, когда в этом множестве существует последовательность, сходящаяся к х0. В топологическом пространстве справедливо утверждение: Если последовательность точек множества А топологического пространства (Х,t) сходится к некоторой точке x0ÎX, то Обратное, вообще говоря, не верно. Пример 1. Пусть
КУЛЬТУРНЫЙ МИНИМУМ.
ВОПРОСЫ. 1. Доказать неравенство Буняковского 2. Доказать неравенство Минковского иравенство параллелограмма. 3. Доказать теорему о наименьшем отклонении частичных сумм. 4. Доказать теорему о минимуме невязки. 5. Доказать теорему Грама 6. Доказать, что 7. Доказать, что функционалы 8. Доказать теорему об эквивалентности норм. 9. Сепарабельные пространства. Доказать сепарабельность пространства 10. Сепарабельные пространства. Доказать сепарабельность пространства 11. Что такое открытое, замкнутое множество, точки прикосновения, предельные точки? 12. Что такое дискретное и совершенное множества? Что такое внутренние и граничные точки? 13. Доказать теорему о дополнении открытых множеств. 14. Доказать теорему о замкнутости теоретико – множественных операций над открытыми и замкнутыми множествами. 15. Доказать теорему о включении и теорему о замыкании объединения. 16. Способы задания топологий. Примеры топологий: дискретная, антидискретная. 17. Сходимость в топологических пространствах. Примеры. ЗАДАЧИ.
К какой последовательности она сходится покоординатно? Сходится ли она к тому же пределу в метриках пространств
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1013; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.86.58 (0.008 с.) |

 .
. является точка
является точка 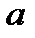 , для последовательности
, для последовательности  (a - фиксированное число) предел равен a, а последовательность
(a - фиксированное число) предел равен a, а последовательность  , где
, где 
 множество натуральных чисел, не имеет предела. В обычной топологии предел последовательности, если он существует, может быть только один, а в топологических пространствах – несколько. Для пространств, не удовлетворяющих каким-нибудь аксиомам отделимости, свойства пределов могут быть весьма необычными. Так, в тривиальных топологических пространствах любая последовательность точек сходится к каждой точке xÎX, так как эта точка х имеет только одну окрестность – все множество Х и эта окрестность содержит все точки последовательности. Носитель может содержать конечное или бесконечное число точек
множество натуральных чисел, не имеет предела. В обычной топологии предел последовательности, если он существует, может быть только один, а в топологических пространствах – несколько. Для пространств, не удовлетворяющих каким-нибудь аксиомам отделимости, свойства пределов могут быть весьма необычными. Так, в тривиальных топологических пространствах любая последовательность точек сходится к каждой точке xÎX, так как эта точка х имеет только одну окрестность – все множество Х и эта окрестность содержит все точки последовательности. Носитель может содержать конечное или бесконечное число точек 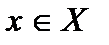 , но топология их не различает.
, но топология их не различает. является пределом натурального ряда. Действительно, зафиксируем произвольную окрестность U точки x. По определению топологии Зарисского, дополнение U до R состоит из конечного числа точек, то есть в U содержится бесконечное число точек. Поскольку в натуральном ряду бесконечное число точек, отсюда следует, что, начиная с некоторого номера N, все точки
является пределом натурального ряда. Действительно, зафиксируем произвольную окрестность U точки x. По определению топологии Зарисского, дополнение U до R состоит из конечного числа точек, то есть в U содержится бесконечное число точек. Поскольку в натуральном ряду бесконечное число точек, отсюда следует, что, начиная с некоторого номера N, все точки  лежат в U.
лежат в U.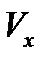 . В этом случае в окрестности
. В этом случае в окрестности 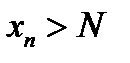 равны x.
равны x. .
. пространство слипшихся точек. Носитель может содержать конечное или бесконечное число точек
пространство слипшихся точек. Носитель может содержать конечное или бесконечное число точек 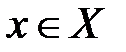 , но топология их не различает. Множество
, но топология их не различает. Множество 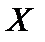 является единственной окрестностью для всех своих точек, поэтому любая последовательность точек
является единственной окрестностью для всех своих точек, поэтому любая последовательность точек  сходится к любой точке множества
сходится к любой точке множества  согласно определению 1.
согласно определению 1. .
. , равномерная сходимость и сходимость в среднем?
, равномерная сходимость и сходимость в среднем? и
и 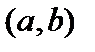 в пространстве
в пространстве 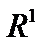 .
. Коши.
Коши. Шмидта.
Шмидта.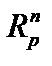
 метрическое пространство.
метрическое пространство.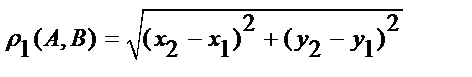 ,
,  ,
,  являются метриками и определить типы пространств.
являются метриками и определить типы пространств. , дискретного метрического пространства, пространства
, дискретного метрического пространства, пространства  .
. , несепарабельность пространства
, несепарабельность пространства  .
. функций бесконечномерно.
функций бесконечномерно. .
. ,
, 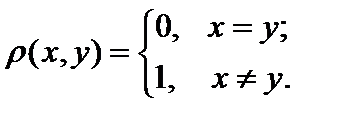 и
и 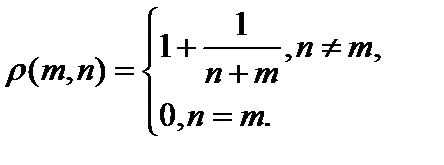 являются метриками.
являются метриками. найти расстояние между функциями
найти расстояние между функциями 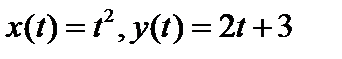 .
.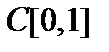 не гильбертово.
не гильбертово.  .
.  при
при  .
.  пространства
пространства  сильнее метрики
сильнее метрики  пространства
пространства 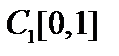 .
. , если
, если  в
в  ?
?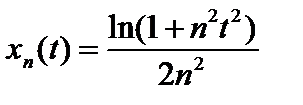 в пространстве
в пространстве  ?
? , полное.
, полное.  .
.  .
. ?
?


