Геометрия эвклидовых пространств
II. ПРОСТРАНСТВА носителей
Комментарий. Главной задачей функционального анализа является изучение свойств бесконечномерных пространств и их отображений. Она возникает как естественное логическое обоснование математики в целом и математического анализа в частности. В линейной алгебре рассматриваются отображения конечномерных векторных пространств. Но во многих случаях, например при решении дифференциальных или интегральных уравнений, возникают отображения бесконечномерных векторных пространств, элементы которых представляются уже не конечными линейными комбинациями, а рядами. Поэтому центральное понятие в бесконечномерном случае  сходимость последовательности элементов носителя (точек) пространства. Чтобы его ввести, нужно каким-то образом наделить пространство способом измерения расстояния между точками, а сами точки сходимость последовательности элементов носителя (точек) пространства. Чтобы его ввести, нужно каким-то образом наделить пространство способом измерения расстояния между точками, а сами точки  числовыми характеристиками. В конечномерных пространствах из фундаментальности последовательности следует сходимость и наоборот числовыми характеристиками. В конечномерных пространствах из фундаментальности последовательности следует сходимость и наоборот  критерий полноты. В бесконечномерных пространствах из фундаментальности последовательности сходимость может не следовать. Поэтому полнота критерий полноты. В бесконечномерных пространствах из фундаментальности последовательности сходимость может не следовать. Поэтому полнота  это ключевой атрибут пространства. это ключевой атрибут пространства.
Пространство в математике  это контекстно определяемое понятие. это контекстно определяемое понятие.
Определение. В под пространством в функциональном анализе понимают пару 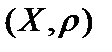 , где , где   носитель пространства, то есть некоторое множество, которое может быть как наделено определённой (например, линейной) структурой, так и нет, а носитель пространства, то есть некоторое множество, которое может быть как наделено определённой (например, линейной) структурой, так и нет, а   заданный на элементах носителя функционал, позволяющий ввести понятие сходимости последовательности элементов носителя. заданный на элементах носителя функционал, позволяющий ввести понятие сходимости последовательности элементов носителя.
Рассмотрим стандартные пространства функционального анализа. На носителе  , не наделённых линейной структурой, можно ввести метрику, свойства которой являются обобщением свойств расстояния между элементами , не наделённых линейной структурой, можно ввести метрику, свойства которой являются обобщением свойств расстояния между элементами  в обычном геометрическом пространстве и построить таким образом метрические пространства. Обобщениемметрическихпространств являются топологические пространства. Любое метрическое пространство в обычном геометрическом пространстве и построить таким образом метрические пространства. Обобщениемметрическихпространств являются топологические пространства. Любое метрическое пространство  топологическое, обратное, вообще говоря, неверно. На носителях топологическое, обратное, вообще говоря, неверно. На носителях  , наделённых линейной структурой, можно ввести как метрику, так и норму (длину) векторов, свойства которой являются обобщением свойств длины векторов в обычном геометрическом пространстве и построить таким образом нормированные пространства. Нормированные пространства всегда метрические и соответственно, топологические. Обратное, вообще говоря, неверно. Это такие пространства, как эвклидовы, гильбертовы и банаховы. Эвклидово пространство , наделённых линейной структурой, можно ввести как метрику, так и норму (длину) векторов, свойства которой являются обобщением свойств длины векторов в обычном геометрическом пространстве и построить таким образом нормированные пространства. Нормированные пространства всегда метрические и соответственно, топологические. Обратное, вообще говоря, неверно. Это такие пространства, как эвклидовы, гильбертовы и банаховы. Эвклидово пространство  это нормированное пространство, где норма вводится через скалярное произведение. Иногда разделяютэвклидовы пространства на собственно эвклидовы (построенные над полем действительных чисел это нормированное пространство, где норма вводится через скалярное произведение. Иногда разделяютэвклидовы пространства на собственно эвклидовы (построенные над полем действительных чисел  ) и унитарные (построенные над полем комплексных чисел ) и унитарные (построенные над полем комплексных чисел  ). Часто бесконечномерныеэвклидовы пространства называют предгильбертовыми, потому, что гильбертовы пространства ). Часто бесконечномерныеэвклидовы пространства называют предгильбертовыми, потому, что гильбертовы пространства  это полные эвклидовы пространства. Банаховы пространства это полные эвклидовы пространства. Банаховы пространства  это полные нормированные пространства. То есть гильбертовы пространства это полные нормированные пространства. То есть гильбертовы пространства  это банаховы пространства, где норма вводится через скалярное произведение. Наиболее общими пространствами, фигурирующими в функциональном анализе, являются топологические пространства. Соотношения между бесконечномерными пространствами отображены на рисунке. это банаховы пространства, где норма вводится через скалярное произведение. Наиболее общими пространствами, фигурирующими в функциональном анализе, являются топологические пространства. Соотношения между бесконечномерными пространствами отображены на рисунке.

Этот текст в этом месте следует рассматривать как программу, потому что задачей этой главы и является определение всех этих пространств и их простейших свойств. К нему следует вернуться в конце главы.
Алгебраические структуры
Определение 1. Пусть М и S два множества произвольной природы, a x,y,z -три элемента, быть может, разных множеств.
Правило (закон), по которому упорядоченной паре элементов х и у ставится в соответствие элемент z (один и только один), называется бинарной операцией или законом композиции, результат этой операции (элемент z) называется композицией, а элементы х и у называются операнды.
Определение 2. Если  (одному из множеств), то закон композиции называется внутренним а множество М называется замкнутым относительно этого закона (этой бинарной операции). (одному из множеств), то закон композиции называется внутренним а множество М называется замкнутым относительно этого закона (этой бинарной операции).
Определение 3. Если операнды принадлежат разным множествам, а композиции  одному из них (например одному из них (например  ), то такая бинарная операция называется внешним законом. ), то такая бинарная операция называется внешним законом.
Комментарий. На множестве М и S может быть определено несколько законов, но все многообразие ситуаций реализуется в простейшем случае, когда их не более двух. Один из них (произвольный) называется аддитивным и обозначается  , другой мультипликативный и обозначается , другой мультипликативный и обозначается 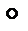 . .
Множество натуральных чисел с обычными операциями сложения, умножения, возведения в степень - примеры внутренних законов, множество действительных чисел и множество векторов в конечномерном пространстве с операцией произведения числа на вектор  внешний закон. В этом пункте нас будут интересовать только внутренние законы композиции. внешний закон. В этом пункте нас будут интересовать только внутренние законы композиции.
Определение 4. А лгебраической структурой  называется множество (носитель структуры) М с заданным на нём одним или двумя внутренними законами композиции, которые обозначаются называется множество (носитель структуры) М с заданным на нём одним или двумя внутренними законами композиции, которые обозначаются  и и  и часто называются “сложение” и “умножение”. и часто называются “сложение” и “умножение”.
Комментарий. Эти законы композиции можно наделить или нет определенными свойствами, которые, в свою очередь, задают ту или иную структуру множества М, которое называется носителем а лгебраической структуры. Имея дело с а лгебраической структурой (АС), следует соблюдать три правила.
1. Природа и характер носителя АС не обсуждается.
2. Природа и характер операций, порождающих данную АС на
множестве М,не обсуждается.
3. Все рассуждения поводятся только на абстрактном уровне. На
уровне интерпретаций (примеров конкретных АС) утверждение может
быть верно, а на абстрактном уровне нет. Обратное  неверно. неверно.
Свойства внутренних законов композиции:
1.   коммутативность. коммутативность.
2.   ассоциативность. ассоциативность.
3.   дистрибутивность дистрибутивность
слева операции  относительно операции относительно операции  . .
4.   дистрибутивность справа операции дистрибутивность справа операции  относительно операции относительно операции  . .
Аналогично определяется дистрибутивность относительно операции  . .
Примеры. 1. Множество действительных чисел с обычными операциями сложения и умножения. Эти операции коммутативны и ассоциативны. Кромке того  и и  , то есть умножение дистрибутивно справа и слева относительно сложения. Но , то есть умножение дистрибутивно справа и слева относительно сложения. Но  и и  , то есть сложение не дистрибутивно ни справа, ни слева относительно операции умножения. , то есть сложение не дистрибутивно ни справа, ни слева относительно операции умножения.
2.   операция возведения в степень не ассоциативна, не коммутативна ( операция возведения в степень не ассоциативна, не коммутативна ( , ,  , но дистрибутивна справа относительно операции умножения ( , но дистрибутивна справа относительно операции умножения ( ) и вообще не имеет смысла дистрибутивность слева относительно умножения. ) и вообще не имеет смысла дистрибутивность слева относительно умножения.
3. Операции  и и  для множеств взаимно дистрибутивны относительно друг друга, ассоциативны и коммутативны. для множеств взаимно дистрибутивны относительно друг друга, ассоциативны и коммутативны.
Комментарий. Законы композиции наделяют элементы множества М некоторыми свойствами, верными или нет только при этих законах. Другими словами, на множестве М при действии данного закона с его свойствами появляются выделенные элементы, т.е. оно становится структуированным (откуда и понятие АС).
Определение 5. Элемент  называется нейтральным относительно данного закона называется нейтральным относительно данного закона  , если , если  . .
Примеры. Ноль на множествах  при сложении, единица при умножении, при сложении, единица при умножении,  при объединении и при пересечении множеств. при объединении и при пересечении множеств.
Ясно, что его может и не быть, например, на множестве  , или нейтральный элемент фактически может быть не определенным элементом множества, а образовывать целый класс элементов этого множества. Рассмотрим, например, множество остатков от деления натурального числа на 3 или, как говорят "вычетов по модулю три". Это множество состоит из классов чисел , или нейтральный элемент фактически может быть не определенным элементом множества, а образовывать целый класс элементов этого множества. Рассмотрим, например, множество остатков от деления натурального числа на 3 или, как говорят "вычетов по модулю три". Это множество состоит из классов чисел  Зададим на этом множестве операцию + с помощью таблицы Кэли (способ задания операций для конечных множеств или классов множеств, заключающийся в непосредственном перечислении результатов операции). Зададим на этом множестве операцию + с помощью таблицы Кэли (способ задания операций для конечных множеств или классов множеств, заключающийся в непосредственном перечислении результатов операции).
| +
| К0
| К1
| К2
| | К0
| К0
| К1
| К2
| | К1
| К1
| К2
| К0
| | К2
| К2
| К0
| К1
| Видно, что  , ,  , ,  . Элемент К0- нейтральный, но фактически он представляет собой бесконечное множество натуральных чисел, нацело делящихся на три. . Элемент К0- нейтральный, но фактически он представляет собой бесконечное множество натуральных чисел, нацело делящихся на три.
Теорема 1. Если нейтральный элемент есть, то он единственен.
 аа. Пусть аа. Пусть 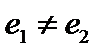 два нейтральных элемента относительно операции два нейтральных элемента относительно операции  . Тогда . Тогда  . Положив в первом равенстве . Положив в первом равенстве  , получим , получим  . Положив во втором равенстве . Положив во втором равенстве  , получим , получим  , то есть , то есть  .■ .■
Определение 6. Пусть множество М содержит нейтральный элемент  относительно операции относительно операции  . Элемент . Элемент  называется симметричным (обратным, противоположным) элементу называется симметричным (обратным, противоположным) элементу 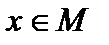 , если , если  . .
Примеры. На множестве (Z,+) нейтральный элемент  , а симметричным , а симметричным 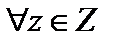 является элемент является элемент  , на множестве , на множестве  нейтральный элемент нейтральный элемент  , но не все , но не все 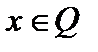 имеет симметричный элемент имеет симметричный элемент  ( ( , то есть элемент , то есть элемент 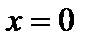 не имеет симметричного), на множестве не имеет симметричного), на множестве  нейтральный элемент нейтральный элемент  , а симметричного нет. , а симметричного нет.
Естественно, нейтральный элемент группоида симметричен, самому себе, т.к. по определению как нейтрального так и симметричного элемента если  , тогда , тогда  , ,  , то есть , то есть 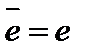 . .
Определяя на множестве произвольной природы М один или два закона композиции, наделяя эти законы какими-то из перечисленных свойств и задавая структуру М относительно этих свойств, мы получим различные АС, перечисленные в таблице, задающей аксиомы АС.
|
| Название АС
| I закон (аддитивный)
| II закон мультипликативный)
|
ассо-циа-тив-ность
| ком-мута-тив-
ность
| Нейт-раль-ный
| сим-
мет-
ричный
| ассо-циа-тив-ность
| ком-мута-тив-
ность
| Нейт-раль-ный
| сим-
мет-
ричный
| |
| Полугруппа
| X
|
|
|
|
|
|
|
| |
| Абелева полугруппа
| X
| X
|
|
|
|
|
|
| |
| Абелева полугруппа с нулем
| X
| X
| X
|
|
|
|
|
| |
| Группа
| X
|
| X
| X
|
|
|
|
|
|
| Абелева группа
| X
| X
| X
| X
|
|
|
|
| |
| Кольцо
| X
| X
| X
| X
| X
|
|
|
| |
| Абелево кольцо
| X
| X
| X
| X
| X
| X
|
|
| |
| Абелево кольцо с единицей
| X
| X
| X
| X
| X
| X
| X
|
| |
| Тело
| X
| X
| X
| X
| X
|
| X
| X
| |
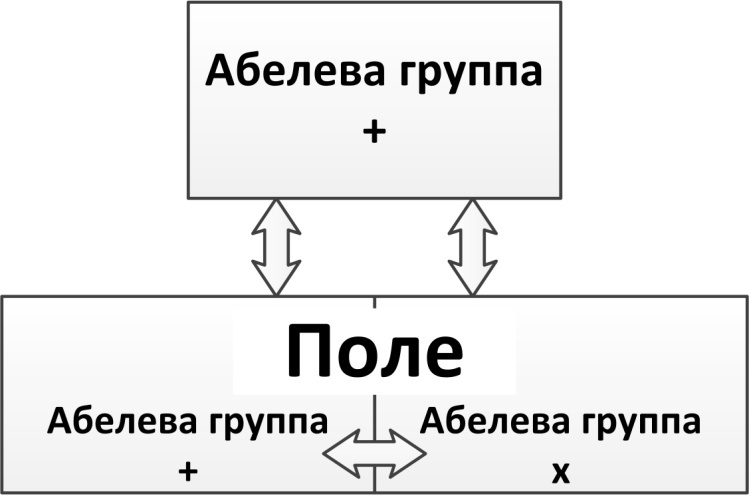
| Поле
| X
| X
| X
| X
| X
| X
| X
| X
| Значёк Х означает, что данный закон обладает этими свойствами, а множество М имеет относительно этого закона соответствующие элементы. При этом полагается, что
1. Мультипликативный закон, если он определен,
дистрибутивен слева и справа относительно аддитивного.
2. Симметричный элемент мультипликативного закона
определен для всех элементов носителя АС (множества М),
кроме нейтрального относительно аддитивного закона.
Линейная структура
Определение 1. Линейной структурой  (линейным пространством, векторным пространством) называют абелеву аддитивную группу (её элементы (линейным пространством, векторным пространством) называют абелеву аддитивную группу (её элементы  называют векторами), определённую над полем произвольной природы (элементы поля называют скалярами называют векторами), определённую над полем произвольной природы (элементы поля называют скалярами 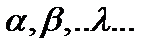 ), причём ), причём 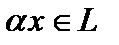 , а естественное согласование между группой и полем обеспечивается аксиомами дистрибутивности: , а естественное согласование между группой и полем обеспечивается аксиомами дистрибутивности:  , ассоциативности по элементам поля , ассоциативности по элементам поля 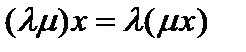 и унитарности и унитарности  . Поле вещественных чисел . Поле вещественных чисел  и поле комплексных чисел и поле комплексных чисел  называют основными полями, полагая, что поле называют основными полями, полагая, что поле  стандартно вложено в поле стандартно вложено в поле  . Если основное поле любое, то его обозначают буквой . Если основное поле любое, то его обозначают буквой  . То есть линейная структура . То есть линейная структура 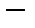 это четвёрка это четвёрка  . .
Комментарий. Для краткости обычно вместо 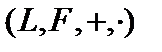 говорят говорят  . Если абелева аддитивная группа определена над любым кольцом, то такая структура называется модулем. Иногда под векторным пространством понимают абелеву аддитивную группу, определённую над телом. Дадим прямое определение линейной структуры . Если абелева аддитивная группа определена над любым кольцом, то такая структура называется модулем. Иногда под векторным пространством понимают абелеву аддитивную группу, определённую над телом. Дадим прямое определение линейной структуры
Определение 1*. Множество  называется линейным пространством (линейной структурой), если для любых двух его элементов x, y определен элемент называется линейным пространством (линейной структурой), если для любых двух его элементов x, y определен элемент  (называемый суммой x и y), и для любого элемента (называемый суммой x и y), и для любого элемента  и любого числа α определен элемент и любого числа α определен элемент  , причем выполнены следующие условия: , причем выполнены следующие условия:
1) для любых элементов  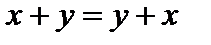 (коммутативность сложения); 2) для любых элементов (коммутативность сложения); 2) для любых элементов  (x+y)+z=x+(y+z) (ассоциативность сложения); 3) существует элемент (x+y)+z=x+(y+z) (ассоциативность сложения); 3) существует элемент  (называемый нулевым элементом, или нулем пространства L) такой, что для любого элемента (называемый нулевым элементом, или нулем пространства L) такой, что для любого элемента   (существование нулевого элемента); 4) для любого элемента (существование нулевого элемента); 4) для любого элемента  существует элемент существует элемент  (называемый обратным к x) такой, что (называемый обратным к x) такой, что  (существование обратного элемента); 5) для любых элементов (существование обратного элемента); 5) для любых элементов  и любого числа α α(x+y)=αx+αy (дистрибутивность умножения суммы элементов на число); 6) для любых чисел и любого числа α α(x+y)=αx+αy (дистрибутивность умножения суммы элементов на число); 6) для любых чисел  любого элемента любого элемента  (α+β)x=αx+βx (дистрибутивность умножения суммы чисел на элемент); 7) для любых (вещественных) чисел α, β и любого элемента (α+β)x=αx+βx (дистрибутивность умножения суммы чисел на элемент); 7) для любых (вещественных) чисел α, β и любого элемента  (αβ)x=α(βx) (ассоциативность умножения на число); 8) для любого элемента (αβ)x=α(βx) (ассоциативность умножения на число); 8) для любого элемента  1x=x (свойство единицы). 1x=x (свойство единицы).
Примеры групп. Примерами групп являются целые, рациональные, действительные, комплексные числа по сложению, ненулевые рациональные, действительные, комплексные числа по умножению. Все эти группы являются абелевыми. Следующий пример групп возникает из векторных пространств. Пусть  — векторное пространство над полем F. Множество невырожденных линейных преобразований векторного пространства — векторное пространство над полем F. Множество невырожденных линейных преобразований векторного пространства  образует группу. Легко проверить, что векторные пространства одинаковой размерности n над одним и тем же полем изоморфны пространству строк длины n, а множество невырожденных линейных преобразований совпадает с множеством невырожденных матриц. образует группу. Легко проверить, что векторные пространства одинаковой размерности n над одним и тем же полем изоморфны пространству строк длины n, а множество невырожденных линейных преобразований совпадает с множеством невырожденных матриц.
Примеры колец. Множество полиномов образуют абелево кольцо с единицей ( ),множество рациональных чисел (нет нейтрального и противоположного элементов по умножению). ),множество рациональных чисел (нет нейтрального и противоположного элементов по умножению).
Примеры линейных структур.
 Два тривиальных пространства: вещественные числа над полем вещественных чисел и нулевое пространство, состоящее из одного нулевого элемента. Два тривиальных пространства: вещественные числа над полем вещественных чисел и нулевое пространство, состоящее из одного нулевого элемента.
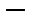 Вещественные числа над телом рациональных чисел; вещественные числа над полем комплексных чисел не образуют векторное пространство (умножение комплексного числа на действительное есть число комплексное). Вещественные числа над телом рациональных чисел; вещественные числа над полем комплексных чисел не образуют векторное пространство (умножение комплексного числа на действительное есть число комплексное).
 Комплексные числа над полем вещественных чисел. Комплексные числа над полем вещественных чисел.
 Полиномы с степени не выше чем n над полем вещественных чисел. Полиномы с степени не выше чем n над полем вещественных чисел.
 Множество конечномерных линейных операторов. Множество конечномерных линейных операторов.
 Множество квадратных матриц. Множество квадратных матриц.
 Множество геометрических векторов на плоскости или в 3-мерном пространстве с обычным понятием равенства (совпадение при параллельном переносе) и обычными операциями сложения векторов и умножением вектора на число. Множество геометрических векторов на плоскости или в 3-мерном пространстве с обычным понятием равенства (совпадение при параллельном переносе) и обычными операциями сложения векторов и умножением вектора на число.
 Множество векторов пространства Множество векторов пространства  и и  , то есть множества, состоящие из всевозможных (упорядоченных) наборов из n чисел (соответственно -- действительных или комплексных). , то есть множества, состоящие из всевозможных (упорядоченных) наборов из n чисел (соответственно -- действительных или комплексных).
 Множество всех непрерывных на заданном промежутке [a, b] функций. Это пространство можно рассматривать как линейное, если определить сумму элементов и умножение на вещественное число обычным образом. Нулевым элементом этого пространства является функция, тождественно равная нулю. Множество всех непрерывных на заданном промежутке [a, b] функций. Это пространство можно рассматривать как линейное, если определить сумму элементов и умножение на вещественное число обычным образом. Нулевым элементом этого пространства является функция, тождественно равная нулю.
 Последовательности Последовательности  вещественных чисел над полем вещественных чисел, удовлетворяющие условию вещественных чисел над полем вещественных чисел, удовлетворяющие условию  . .
 Расширение поля как линейное пространство. Пусть поле Расширение поля как линейное пространство. Пусть поле  включено в поле включено в поле  , то есть , то есть  . Тогда поле . Тогда поле  можно рассматривать как линейное пространство над полем можно рассматривать как линейное пространство над полем  , так как , так как 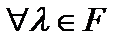 и и  определено произведение определено произведение 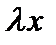 по определению поля по определению поля  , а все аксиомы линейного пространства над полем , а все аксиомы линейного пространства над полем  выполнены, так как это аксиомы поля выполнены, так как это аксиомы поля  . .
Для произвольного линейного пространства  , как идля пространства , как идля пространства  , можно ввести понятие линейной зависимости и независимости системы векторов линейного пространства , можно ввести понятие линейной зависимости и независимости системы векторов линейного пространства  и, соответственно, понятие о размерности линейного пространства и, соответственно, понятие о размерности линейного пространства  . Достаточно вместо векторов из пространства . Достаточно вместо векторов из пространства  говорить о векторах из линейного пространства говорить о векторах из линейного пространства  . .
Определение 2. Линейное пространство  называют бесконечномерным, если для любого натурального числа N в нём имеется система из N штук линейно независимых векторов. называют бесконечномерным, если для любого натурального числа N в нём имеется система из N штук линейно независимых векторов.
Пример. 1. Покажем, что бесконечномерным является линейное пространство всех непрерывных (как и интегрируемых) на сегменте  функций. функций.
 1. В силу определения 2 достаточно доказать, что на сегменте 1. В силу определения 2 достаточно доказать, что на сегменте  существует любое целое положительное число линейно-независимых элементов. Действительно, этому пространству принадлежат функции существует любое целое положительное число линейно-независимых элементов. Действительно, этому пространству принадлежат функции  . Это система линейно-независимых векторов для любых . Это система линейно-независимых векторов для любых  . Действительно, возьмём производные вещественного числа . Действительно, возьмём производные вещественного числа  , составим линейную комбинацию , составим линейную комбинацию  , приравняем её к , приравняем её к  - вектору, а нейтральным элементом будет функция, тождественно равная нулю на - вектору, а нейтральным элементом будет функция, тождественно равная нулю на  . Многочлен степени . Многочлен степени  на на  может иметь не более, чем может иметь не более, чем  корней, а он тождественно равен нулю. Следовательно, нулевыми являются коэффициенты. Итак, равенство нулю линейной комбинации влечёт за собой равенство нулю всех коэффициентов линейной комбинации, значит, система векторов корней, а он тождественно равен нулю. Следовательно, нулевыми являются коэффициенты. Итак, равенство нулю линейной комбинации влечёт за собой равенство нулю всех коэффициентов линейной комбинации, значит, система векторов  линейно независима. линейно независима.
2. Покажем это иначе. Пусть n – произвольное натуральное число. Положим:

Докажем, что система векторов 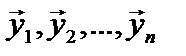 является линейно независимой. Запишем равенство. является линейно независимой. Запишем равенство.
 . .
Положив последовательно  , , 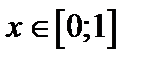 , получим , получим
 . Таким образом, равенство . Таким образом, равенство
 влечет за собой равенство влечет за собой равенство  . Отсюда, векторы . Отсюда, векторы  линейно независимы. Так как n – любое натуральное число, то, следовательно, векторное пространство всех непрерывных функций заданных на отрезке линейно независимы. Так как n – любое натуральное число, то, следовательно, векторное пространство всех непрерывных функций заданных на отрезке  не имеет конечной системы линейно независимых векторов, для которых всякая система, содержащая на один вектор больше, была бы линейно зависима. Поэтому в этом пространстве нельзя ввести понятие конечной размерности. не имеет конечной системы линейно независимых векторов, для которых всякая система, содержащая на один вектор больше, была бы линейно зависима. Поэтому в этом пространстве нельзя ввести понятие конечной размерности. 
ЭВКЛИДОВЫ ПРОСТРАНСТВА
Комментарий. В линейных структурах не определены длины векторов, углы между векторами, то есть нет возможности для измерений. Эту возможность даёт введение понятия абстрактного скалярного произведения как обобщения понятия скалярного произведения векторов.
2.3.1. Определения и примеры
Определение 1. Пусть задана линейная структура  , где , где  , поле , поле  совпадает или с полем действительных чисел совпадает или с полем действительных чисел  или с полем комплексных чисел или с полем комплексных чисел  . Говорят, что на линейной структуре . Говорят, что на линейной структуре  задано скалярное произведение задано скалярное произведение  , если , если  указан функционал, ставящий в соответствие этим элементам действительное или комплексное число, удовлетворяющее аксиомам (легко доказываемым для обычных геометрических векторов): 1) указан функционал, ставящий в соответствие этим элементам действительное или комплексное число, удовлетворяющее аксиомам (легко доказываемым для обычных геометрических векторов): 1) 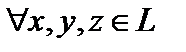 и и  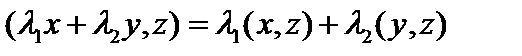 (линейность по первому аргументу); 2) (линейность по первому аргументу); 2)  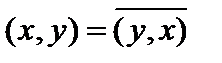 где черта означает комплексное сопряжение (эрмитова симметричность); 3) где черта означает комплексное сопряжение (эрмитова симметричность); 3) 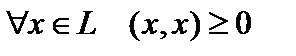 ,причем ,причем 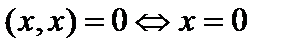 (унитарность скалярного произведения). Действительное линейное пространство со скалярным произведением называется эвклидовым пространством (унитарность скалярного произведения). Действительное линейное пространство со скалярным произведением называется эвклидовым пространством  , комплексное , комплексное  унитарным. унитарным.

Комментарий. В определении 1 мы абстрагируемся не только от природы изучаемых элементов и конкретного вида правил образования суммы элементов и произведения элемента на действительное число, но и от конкретного вида правила образования скалярного произведения двух элементов. Важно лишь, чтобы указанные правила удовлетворяли восьми аксиомам. Бесконечномерныеэвклидовы пространства часто называют предгильбертовыми. В эвклидовом пространствескалярное произведение  коммутативно, то есть коммутативно, то есть  и линейно и по второму аргументу. Сложнее с унитарным пространством. Здесь и линейно и по второму аргументу. Сложнее с унитарным пространством. Здесь  . .
Определение 2. Введение на линейной структуре  скалярного произведения скалярного произведения  позволяет определить в эвклидовом пространстве эвклидову норму его элементов: позволяет определить в эвклидовом пространстве эвклидову норму его элементов:  (как аналог длины вектора). (как аналог длины вектора).
Пример. В пространстве непрерывных функций  определим скалярное произведение определим скалярное произведение  . Покажем, что это . Покажем, что это 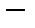 скалярное произведение. скалярное произведение.
 Из свойств интеграла очевидно выполнение первых двух аксиом. Покажем унитарность. По теореме о среднем Из свойств интеграла очевидно выполнение первых двух аксиом. Покажем унитарность. По теореме о среднем  . Покажем, что . Покажем, что  . Если . Если  , то и , то и  . Покажем обратное. Пусть . Покажем обратное. Пусть  . Покажем, что . Покажем, что  . .  . Пусть . Пусть  . Тогда по теореме о сохранении знака непрерывной функции . Тогда по теореме о сохранении знака непрерывной функции 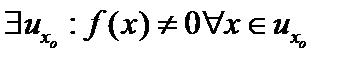 . Но тогда . Но тогда  . Эвклидова норма элементов в пространстве . Эвклидова норма элементов в пространстве   . . 
Комментарий. Скалярное произведение в этом пространстве можно определить, например, как  или как или как 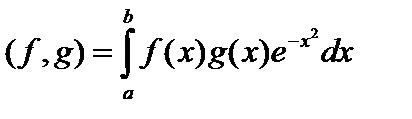 . Так как скалярное произведение можно ввести различными способами, то и нормы тоже отличаются между собой (удава можно мерить и мартышками и попугаями). . Так как скалярное произведение можно ввести различными способами, то и нормы тоже отличаются между собой (удава можно мерить и мартышками и попугаями).
Полнота в смысле Фреше
Определение 1. Последовательность точек  эвклидова пространства сходится по норме к точке эвклидова пространства сходится по норме к точке  , если числовая последовательность , если числовая последовательность  , то есть , то есть 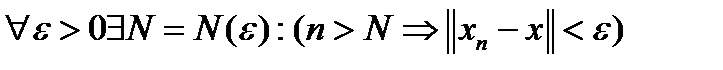 . Обозначение используется обычное: . Обозначение используется обычное:  . .
Определение 2. Пусть множество M есть подмножество множества Е. Точка  называется предельной точкой множества M, если существует последовательность точек множества M, с попарно различными элементами, сходящаяся к x. называется предельной точкой множества M, если существует последовательность точек множества M, с попарно различными элементами, сходящаяся к x.
Комментарий. Чтобы точка  была предельнойточкой множества M, надо каким была предельнойточкой множества M, надо каким  либо образом исключить стационарные последовательности либо образом исключить стационарные последовательности  , чтобы изолированные точки множества , чтобы изолированные точки множества  , то есть точки, у которых существует окрестность, не содержащая точек из множества , то есть точки, у которых существует окрестность, не содержащая точек из множества  , не могли оказаться предельными. В этом определении представлен один из таких вариантов. , не могли оказаться предельными. В этом определении представлен один из таких вариантов.
Определение 3. Пусть множество  . Множество . Множество  называется замыканием множества называется замыканием множества  , если для любой точки , если для любой точки 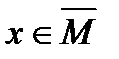 существует последовательность не обязательно различных точек из множества существует последовательность не обязательно различных точек из множества  , сходящихся к точке х. , сходящихся к точке х.
Определение 4. Множество называется замкнутым, если оно совпадает со своим замыканием то есть  . .
Комментарий. В определении допускаются стационарные, начиная с некоторого номера, последовательности. Поэтому любая изолированная точка множества  замкнута. Позже мы рассмотрим этот вопрос подробнее. замкнута. Позже мы рассмотрим этот вопрос подробнее.
Определение 5. Последовательность точек xn эвклидова пространства  называется фундаментальной, если называется фундаментальной, если  . .
Определение 5*. Последовательность точек xn эвклидова пространства  называется фундаментальной, если называется фундаментальной, если 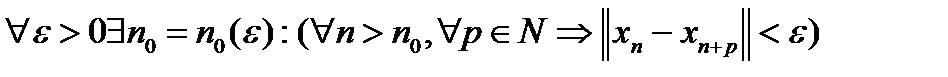 . .
Теорема 1. Последовательность точек  эвклидова пространства фундаментальна, если она сходится по норме к точке эвклидова пространства фундаментальна, если она сходится по норме к точке  . .
 Пусть Пусть  . Тогда . Тогда  . Выберем произвольные . Выберем произвольные  . Тогда из неравенства треугольника . Тогда из неравенства треугольника  . . 
Комментарий. Обратное, вообще говоря, неверно. Рассмотрим примеры.
Примеры. 1. Рассмотрим в пространстве всех интегрируемых по Риману функций  на сегменте на сегменте  подпространство, состоящее из всех многочленов. Пусть подпространство, состоящее из всех многочленов. Пусть 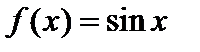 . Согласно формуле Тейлора с остаточным членом в форме Лагранжа можем записать . Согласно формуле Тейлора с остаточным членом в форме Лагранжа можем записать  , где , где  .Обозначим через Pn (x) сум .Обозначим через Pn (x) сум
|



 сходимость последовательности элементов носителя (точек) пространства. Чтобы его ввести, нужно каким-то образом наделить пространство способом измерения расстояния между точками, а сами точки
сходимость последовательности элементов носителя (точек) пространства. Чтобы его ввести, нужно каким-то образом наделить пространство способом измерения расстояния между точками, а сами точки 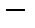 числовыми характеристиками. В конечномерных пространствах из фундаментальности последовательности следует сходимость и наоборот
числовыми характеристиками. В конечномерных пространствах из фундаментальности последовательности следует сходимость и наоборот  это контекстно определяемое понятие.
это контекстно определяемое понятие.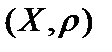 , где
, где 
 носитель пространства, то есть некоторое множество, которое может быть как наделено определённой (например, линейной) структурой, так и нет, а
носитель пространства, то есть некоторое множество, которое может быть как наделено определённой (например, линейной) структурой, так и нет, а 
 в обычном геометрическом пространстве и построить таким образом метрические пространства. Обобщениемметрическихпространств являются топологические пространства. Любое метрическое пространство
в обычном геометрическом пространстве и построить таким образом метрические пространства. Обобщениемметрическихпространств являются топологические пространства. Любое метрическое пространство  топологическое, обратное, вообще говоря, неверно. На носителях
топологическое, обратное, вообще говоря, неверно. На носителях  ) и унитарные (построенные над полем комплексных чисел
) и унитарные (построенные над полем комплексных чисел  ). Часто бесконечномерныеэвклидовы пространства называют предгильбертовыми, потому, что гильбертовы пространства
). Часто бесконечномерныеэвклидовы пространства называют предгильбертовыми, потому, что гильбертовы пространства  (одному из множеств), то закон композиции называется внутренним а множество М называется замкнутым относительно этого закона (этой бинарной операции).
(одному из множеств), то закон композиции называется внутренним а множество М называется замкнутым относительно этого закона (этой бинарной операции). ), то такая бинарная операция называется внешним законом.
), то такая бинарная операция называется внешним законом. , другой мультипликативный и обозначается
, другой мультипликативный и обозначается 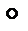 .
. называется множество (носитель структуры) М с заданным на нём одним или двумя внутренними законами композиции, которые обозначаются
называется множество (носитель структуры) М с заданным на нём одним или двумя внутренними законами композиции, которые обозначаются  и
и  и часто называются “сложение” и “умножение”.
и часто называются “сложение” и “умножение”.
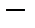 коммутативность.
коммутативность.
 ассоциативность.
ассоциативность.
 дистрибутивность
дистрибутивность относительно операции
относительно операции 
 дистрибутивность справа операции
дистрибутивность справа операции  и
и  , то есть умножение дистрибутивно справа и слева относительно сложения. Но
, то есть умножение дистрибутивно справа и слева относительно сложения. Но  и
и  , то есть сложение не дистрибутивно ни справа, ни слева относительно операции умножения.
, то есть сложение не дистрибутивно ни справа, ни слева относительно операции умножения. 
 ,
,  , но дистрибутивна справа относительно операции умножения (
, но дистрибутивна справа относительно операции умножения ( ) и вообще не имеет смысла дистрибутивность слева относительно умножения.
) и вообще не имеет смысла дистрибутивность слева относительно умножения. и
и  для множеств взаимно дистрибутивны относительно друг друга, ассоциативны и коммутативны.
для множеств взаимно дистрибутивны относительно друг друга, ассоциативны и коммутативны. называется нейтральным относительно данного закона
называется нейтральным относительно данного закона  .
. при сложении, единица при умножении,
при сложении, единица при умножении,  при объединении и при пересечении множеств.
при объединении и при пересечении множеств. , или нейтральный элемент фактически может быть не определенным элементом множества, а образовывать целый класс элементов этого множества. Рассмотрим, например, множество остатков от деления натурального числа на 3 или, как говорят "вычетов по модулю три". Это множество состоит из классов чисел
, или нейтральный элемент фактически может быть не определенным элементом множества, а образовывать целый класс элементов этого множества. Рассмотрим, например, множество остатков от деления натурального числа на 3 или, как говорят "вычетов по модулю три". Это множество состоит из классов чисел  Зададим на этом множестве операцию + с помощью таблицы Кэли (способ задания операций для конечных множеств или классов множеств, заключающийся в непосредственном перечислении результатов операции).
Зададим на этом множестве операцию + с помощью таблицы Кэли (способ задания операций для конечных множеств или классов множеств, заключающийся в непосредственном перечислении результатов операции). ,
,  ,
,  . Элемент К0- нейтральный, но фактически он представляет собой бесконечное множество натуральных чисел, нацело делящихся на три.
. Элемент К0- нейтральный, но фактически он представляет собой бесконечное множество натуральных чисел, нацело делящихся на три. аа. Пусть
аа. Пусть 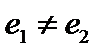 два нейтральных элемента относительно операции
два нейтральных элемента относительно операции  . Положив в первом равенстве
. Положив в первом равенстве  , получим
, получим  . Положив во втором равенстве
. Положив во втором равенстве  , получим
, получим  , то есть
, то есть  .■
.■ называется симметричным (обратным, противоположным) элементу
называется симметричным (обратным, противоположным) элементу 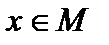 , если
, если  .
. , а симметричным
, а симметричным 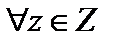 является элемент
является элемент  , на множестве
, на множестве  нейтральный элемент
нейтральный элемент  , но не все
, но не все 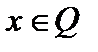 имеет симметричный элемент
имеет симметричный элемент  (
( , то есть элемент
, то есть элемент 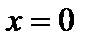 не имеет симметричного), на множестве
не имеет симметричного), на множестве  нейтральный элемент
нейтральный элемент  , тогда
, тогда  ,
,  , то есть
, то есть 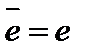 .
. (линейным пространством, векторным пространством) называют абелеву аддитивную группу (её элементы
(линейным пространством, векторным пространством) называют абелеву аддитивную группу (её элементы  называют векторами), определённую над полем произвольной природы (элементы поля называют скалярами
называют векторами), определённую над полем произвольной природы (элементы поля называют скалярами 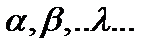 ), причём
), причём 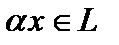 , а естественное согласование между группой и полем обеспечивается аксиомами дистрибутивности:
, а естественное согласование между группой и полем обеспечивается аксиомами дистрибутивности:  , ассоциативности по элементам поля
, ассоциативности по элементам поля 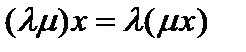 и унитарности
и унитарности  . Поле вещественных чисел
. Поле вещественных чисел  . То есть линейная структура
. То есть линейная структура 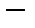 это четвёрка
это четвёрка  .
.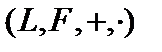 говорят
говорят 
 (называемый суммой x и y), и для любого элемента
(называемый суммой x и y), и для любого элемента  и любого числа α определен элемент
и любого числа α определен элемент  , причем выполнены следующие условия:
, причем выполнены следующие условия: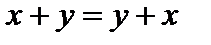 (коммутативность сложения); 2) для любых элементов
(коммутативность сложения); 2) для любых элементов  (x+y)+z=x+(y+z) (ассоциативность сложения); 3) существует элемент
(x+y)+z=x+(y+z) (ассоциативность сложения); 3) существует элемент  (называемый нулевым элементом, или нулем пространства L) такой, что для любого элемента
(называемый нулевым элементом, или нулем пространства L) такой, что для любого элемента  (существование нулевого элемента); 4) для любого элемента
(существование нулевого элемента); 4) для любого элемента  (называемый обратным к x) такой, что
(называемый обратным к x) такой, что  (существование обратного элемента); 5) для любых элементов
(существование обратного элемента); 5) для любых элементов  любого элемента
любого элемента  ),множество рациональных чисел (нет нейтрального и противоположного элементов по умножению).
),множество рациональных чисел (нет нейтрального и противоположного элементов по умножению). Два тривиальных пространства: вещественные числа над полем вещественных чисел и нулевое пространство, состоящее из одного нулевого элемента.
Два тривиальных пространства: вещественные числа над полем вещественных чисел и нулевое пространство, состоящее из одного нулевого элемента.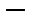 Вещественные числа над телом рациональных чисел; вещественные числа над полем комплексных чисел не образуют векторное пространство (умножение комплексного числа на действительное есть число комплексное).
Вещественные числа над телом рациональных чисел; вещественные числа над полем комплексных чисел не образуют векторное пространство (умножение комплексного числа на действительное есть число комплексное). Комплексные числа над полем вещественных чисел.
Комплексные числа над полем вещественных чисел. Полиномы с степени не выше чем n над полем вещественных чисел.
Полиномы с степени не выше чем n над полем вещественных чисел. Множество конечномерных линейных операторов.
Множество конечномерных линейных операторов. Множество квадратных матриц.
Множество квадратных матриц. Множество геометрических векторов на плоскости или в 3-мерном пространстве с обычным понятием равенства (совпадение при параллельном переносе) и обычными операциями сложения векторов и умножением вектора на число.
Множество геометрических векторов на плоскости или в 3-мерном пространстве с обычным понятием равенства (совпадение при параллельном переносе) и обычными операциями сложения векторов и умножением вектора на число. Множество векторов пространства
Множество векторов пространства  и
и  , то есть множества, состоящие из всевозможных (упорядоченных) наборов из n чисел (соответственно -- действительных или комплексных).
, то есть множества, состоящие из всевозможных (упорядоченных) наборов из n чисел (соответственно -- действительных или комплексных). Множество всех непрерывных на заданном промежутке [a, b] функций. Это пространство можно рассматривать как линейное, если определить сумму элементов и умножение на вещественное число обычным образом. Нулевым элементом этого пространства является функция, тождественно равная нулю.
Множество всех непрерывных на заданном промежутке [a, b] функций. Это пространство можно рассматривать как линейное, если определить сумму элементов и умножение на вещественное число обычным образом. Нулевым элементом этого пространства является функция, тождественно равная нулю. Последовательности
Последовательности  вещественных чисел над полем вещественных чисел, удовлетворяющие условию
вещественных чисел над полем вещественных чисел, удовлетворяющие условию  .
. , то есть
, то есть  . Тогда поле
. Тогда поле 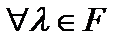 и
и  определено произведение
определено произведение 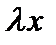 по определению поля
по определению поля  функций.
функций. 1. В силу определения 2 достаточно доказать, что на сегменте
1. В силу определения 2 достаточно доказать, что на сегменте  . Это система линейно-независимых векторов для любых
. Это система линейно-независимых векторов для любых  . Действительно, возьмём производные вещественного числа
. Действительно, возьмём производные вещественного числа  , составим линейную комбинацию
, составим линейную комбинацию  , приравняем её к
, приравняем её к  - вектору, а нейтральным элементом будет функция, тождественно равная нулю на
- вектору, а нейтральным элементом будет функция, тождественно равная нулю на  на
на  линейно независима.
линейно независима.
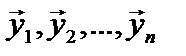 является линейно независимой. Запишем равенство.
является линейно независимой. Запишем равенство. .
. ,
, 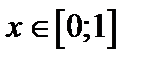 , получим
, получим . Таким образом, равенство
. Таким образом, равенство влечет за собой равенство
влечет за собой равенство  . Отсюда, векторы
. Отсюда, векторы  линейно независимы. Так как n – любое натуральное число, то, следовательно, векторное пространство всех непрерывных функций заданных на отрезке
линейно независимы. Так как n – любое натуральное число, то, следовательно, векторное пространство всех непрерывных функций заданных на отрезке  , поле
, поле  , если
, если  указан функционал, ставящий в соответствие этим элементам действительное или комплексное число, удовлетворяющее аксиомам (легко доказываемым для обычных геометрических векторов): 1)
указан функционал, ставящий в соответствие этим элементам действительное или комплексное число, удовлетворяющее аксиомам (легко доказываемым для обычных геометрических векторов): 1) 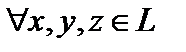 и
и 
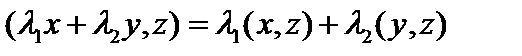 (линейность по первому аргументу); 2)
(линейность по первому аргументу); 2) 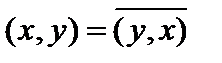 где черта означает комплексное сопряжение (эрмитова симметричность); 3)
где черта означает комплексное сопряжение (эрмитова симметричность); 3) 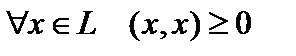 ,причем
,причем 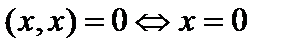 (унитарность скалярного произведения). Действительное линейное пространство со скалярным произведением называется эвклидовым пространством
(унитарность скалярного произведения). Действительное линейное пространство со скалярным произведением называется эвклидовым пространством  , комплексное
, комплексное 
 и линейно и по второму аргументу. Сложнее с унитарным пространством. Здесь
и линейно и по второму аргументу. Сложнее с унитарным пространством. Здесь  .
. (как аналог длины вектора).
(как аналог длины вектора). определим скалярное произведение
определим скалярное произведение  . Покажем, что это
. Покажем, что это 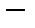 скалярное произведение.
скалярное произведение. Из свойств интеграла очевидно выполнение первых двух аксиом. Покажем унитарность. По теореме о среднем
Из свойств интеграла очевидно выполнение первых двух аксиом. Покажем унитарность. По теореме о среднем  . Покажем, что
. Покажем, что  . Если
. Если  , то и
, то и  . Покажем обратное. Пусть
. Покажем обратное. Пусть  .
.  . Пусть
. Пусть  . Тогда по теореме о сохранении знака непрерывной функции
. Тогда по теореме о сохранении знака непрерывной функции 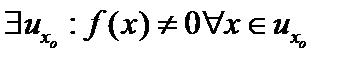 . Но тогда
. Но тогда  . Эвклидова норма элементов в пространстве
. Эвклидова норма элементов в пространстве  .
. 
 или как
или как 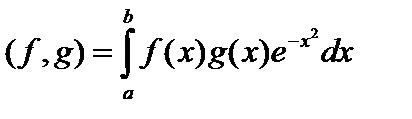 . Так как скалярное произведение можно ввести различными способами, то и нормы тоже отличаются между собой (удава можно мерить и мартышками и попугаями).
. Так как скалярное произведение можно ввести различными способами, то и нормы тоже отличаются между собой (удава можно мерить и мартышками и попугаями). эвклидова пространства сходится по норме к точке
эвклидова пространства сходится по норме к точке  , если числовая последовательность
, если числовая последовательность  , то есть
, то есть 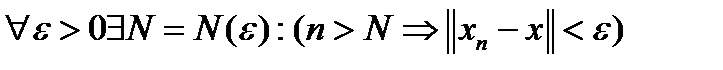 . Обозначение используется обычное:
. Обозначение используется обычное:  .
. называется предельной точкой множества M, если существует последовательность точек множества M, с попарно различными элементами, сходящаяся к x.
называется предельной точкой множества M, если существует последовательность точек множества M, с попарно различными элементами, сходящаяся к x. либо образом исключить стационарные последовательности
либо образом исключить стационарные последовательности  , чтобы изолированные точки множества
, чтобы изолированные точки множества  , то есть точки, у которых существует окрестность, не содержащая точек из множества
, то есть точки, у которых существует окрестность, не содержащая точек из множества  . Множество
. Множество  называется замыканием множества
называется замыканием множества 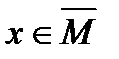 существует последовательность не обязательно различных точек из множества
существует последовательность не обязательно различных точек из множества  .
. называется фундаментальной, если
называется фундаментальной, если  .
.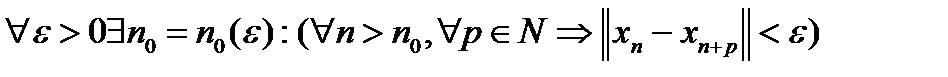 .
. Пусть
Пусть  . Тогда
. Тогда  . Выберем произвольные
. Выберем произвольные  . Тогда из неравенства треугольника
. Тогда из неравенства треугольника  .
. 
 на сегменте
на сегменте  подпространство, состоящее из всех многочленов. Пусть
подпространство, состоящее из всех многочленов. Пусть 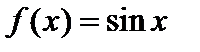 . Согласно формуле Тейлора с остаточным членом в форме Лагранжа можем записать
. Согласно формуле Тейлора с остаточным членом в форме Лагранжа можем записать  , где
, где  .Обозначим через Pn (x) сум
.Обозначим через Pn (x) сум 


